時系列
ユーザーガイドのこのセクションでは、ストリーミング式および数式で使用できる時系列機能の概要を説明します。
時系列集計
timeseries 関数は、Solr に組み込まれているファセット機能と日付演算機能を活用して、高速な分散時系列集計を実行します。
以下の例では、日次株価データのコレクションに対して、月次の時系列集計を実行します。この例では、特定の期間における株式ティッカー AMZN の月間平均終値を計算します。
timeseries(stocks,
q=ticker_s:amzn,
field="date_dt",
start="2010-01-01T00:00:00Z",
end="2017-11-01T00:00:00Z",
gap="+1MONTH",
format="YYYY-MM",
avg(close_d))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"date_dt": "2010-01",
"avg(close_d)": 127.42315789473685
},
{
"date_dt": "2010-02",
"avg(close_d)": 118.02105263157895
},
{
"date_dt": "2010-03",
"avg(close_d)": 130.89739130434782
},
{
"date_dt": "2010-04",
"avg(close_d)": 141.07
},
{
"date_dt": "2010-05",
"avg(close_d)": 127.606
},
{
"date_dt": "2010-06",
"avg(close_d)": 121.66681818181816
},
{
"date_dt": "2010-07",
"avg(close_d)": 117.5190476190476
}
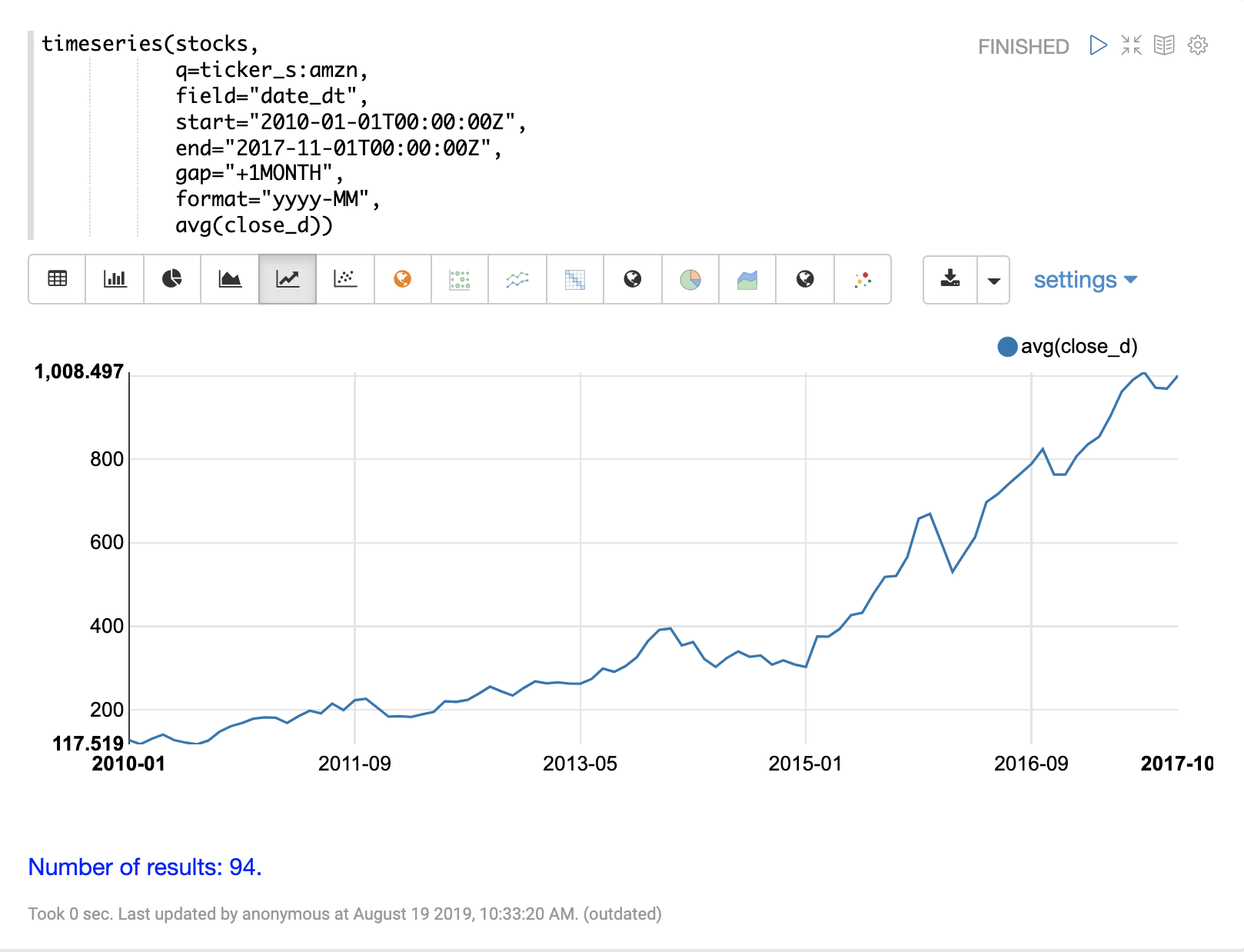
]}}Zeppelin-Solr を使用すると、この時系列を折れ線グラフで視覚化できます。
時系列のベクトル化
時系列を平滑化またはモデル化する前に、データをベクトル化する必要があります。col 関数を使用して、タプルのリストからデータの列を配列にコピーできます。
以下の式は、date_dt フィールドと avg(close_d) フィールドのベクトル化を示しています。次に、zplot 関数を使用して、x 軸に月、y 軸に平均終値をプロットします。
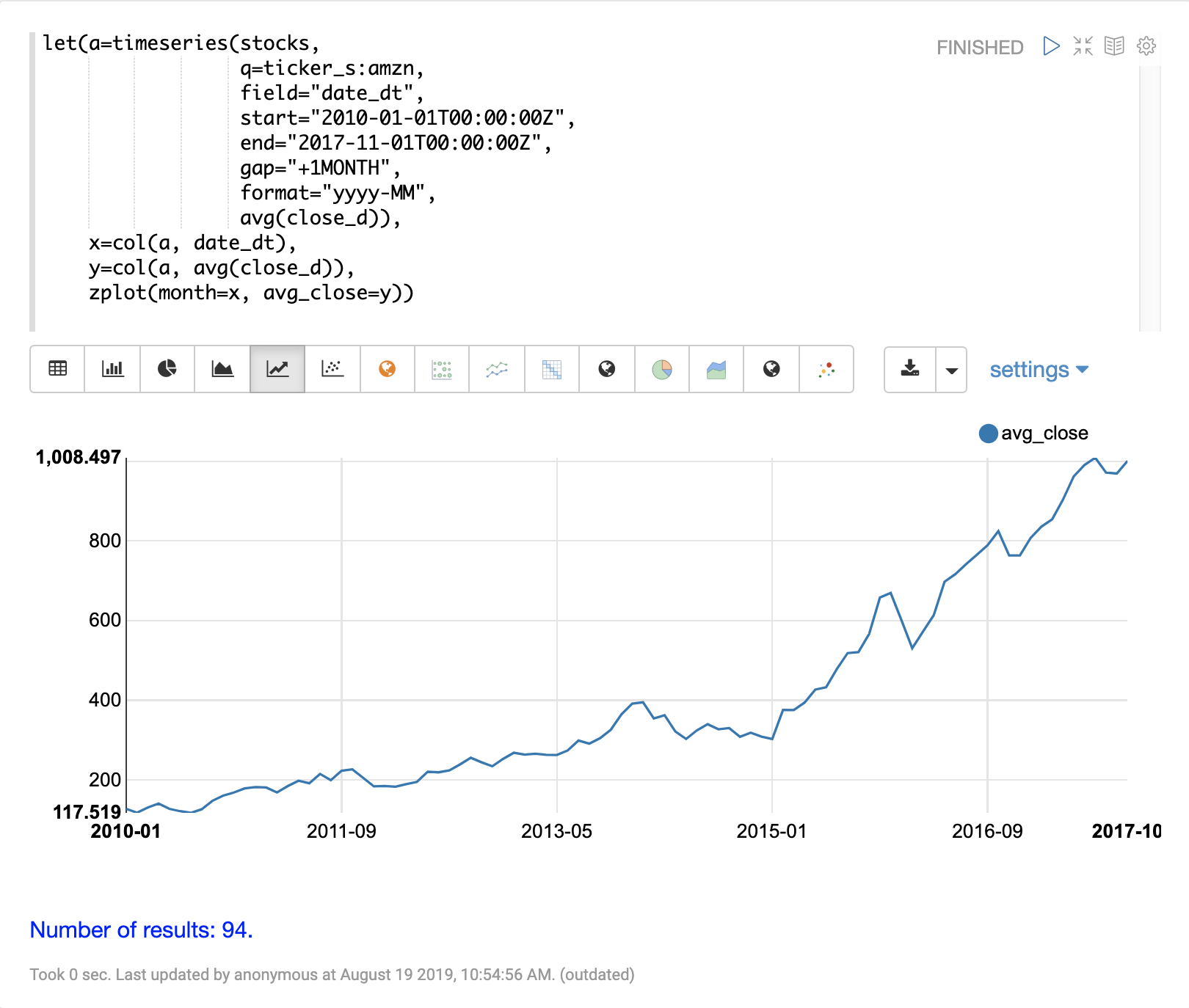
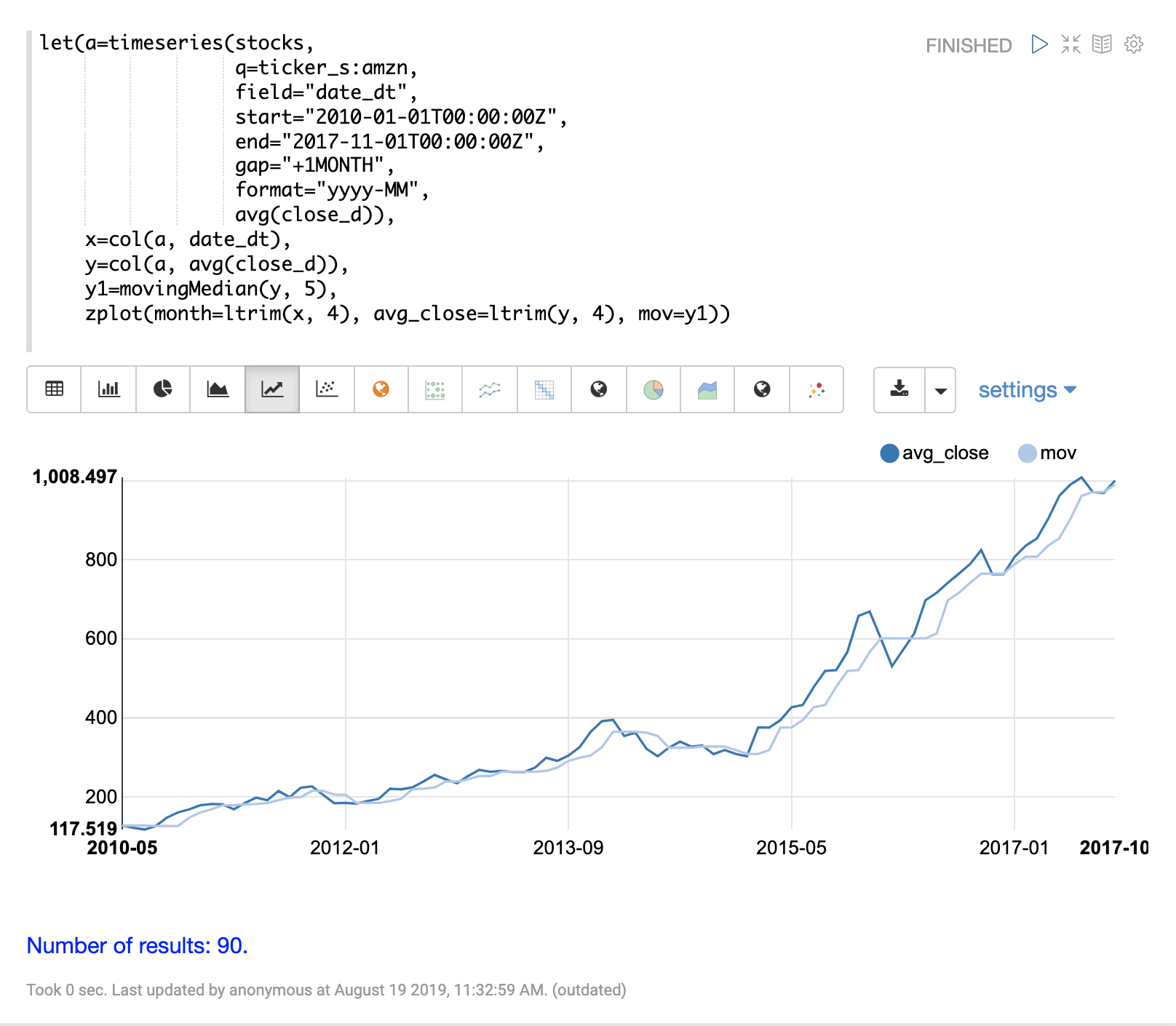
平滑化
時系列の平滑化は、時系列からノイズを除去し、根本的な傾向を特定するのに役立つことがよくあります。数式ライブラリには、時系列平滑化のための 3 つの**スライディングウィンドウ**アプローチがあります。これらのアプローチでは、データのスライディングウィンドウからの要約値を使用して、平滑化された新しいデータポイントのセットを計算します。
3 つの**スライディングウィンドウ**関数は遅行指標であり、これは、傾向がスライディングウィンドウの要約値に影響を与えるまで、傾向の方向に動き始めないことを意味します。この遅行特性により、これらの平滑化関数は、傾向の方向を確認するためによく使用されます。
移動平均
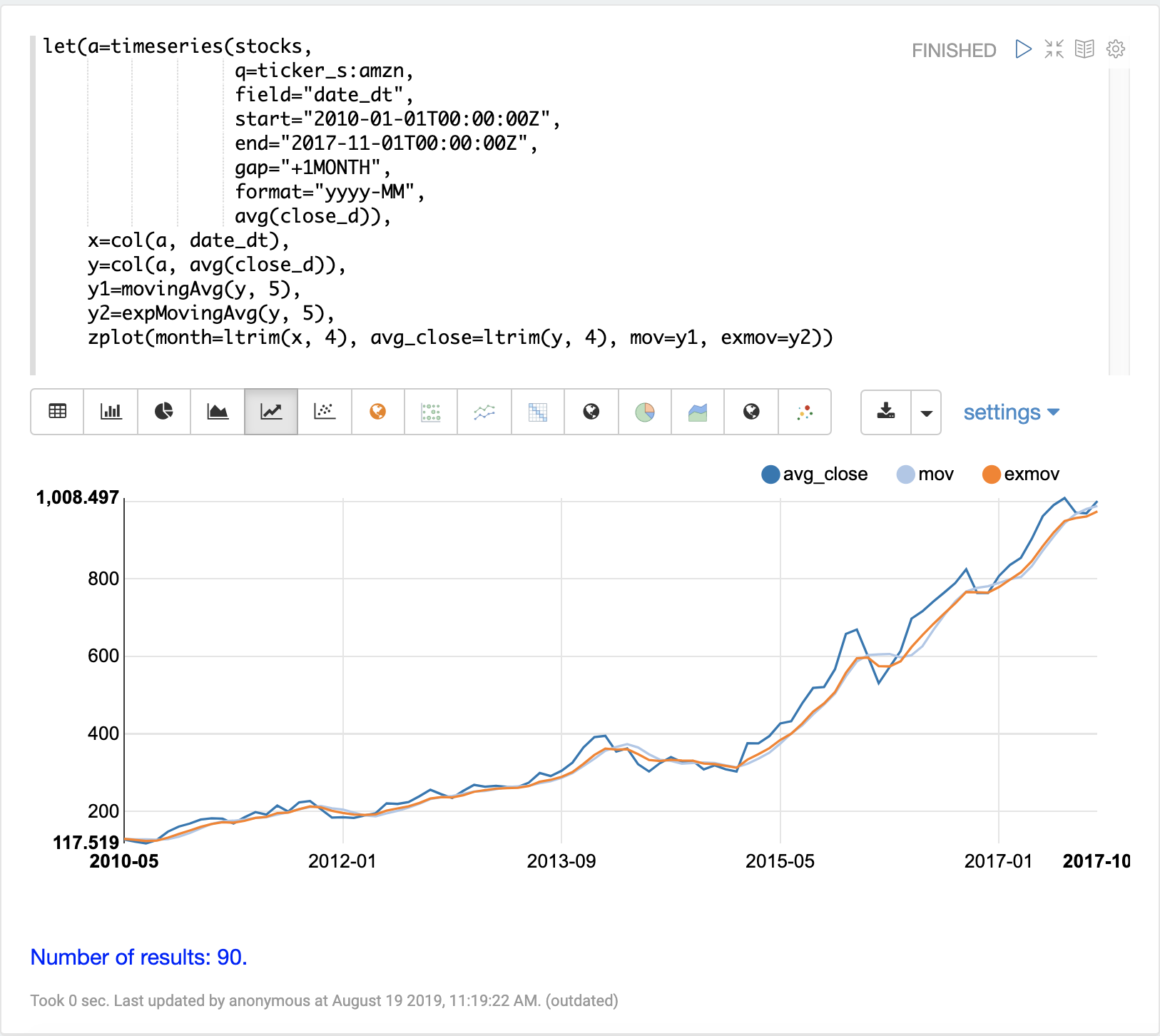
movingAvg 関数は、データのスライディングウィンドウ上で単純移動平均を計算します。以下の例では、時系列を生成し、avg(close_d) フィールドをベクトル化し、ウィンドウサイズ 5 で移動平均を計算します。
移動平均関数は、元のベクトルよりも短い長さの配列を返します。これは、平均の計算にデータのフルウィンドウが利用可能になった場合にのみ結果が生成されるためです。ウィンドウサイズが 5 の場合、移動平均は 5 番目の値で結果の生成を開始します。それ以前の値は結果に含まれません。
次に、zplot 関数を使用して、x 軸に月を、y 軸に平均終値と移動平均をプロットします。ltrim 関数を使用して、x 軸と平均終値から最初の 4 つの値を切り捨てます。これは、3 つの配列を 5 番目の値から開始するように揃えるために行われます。
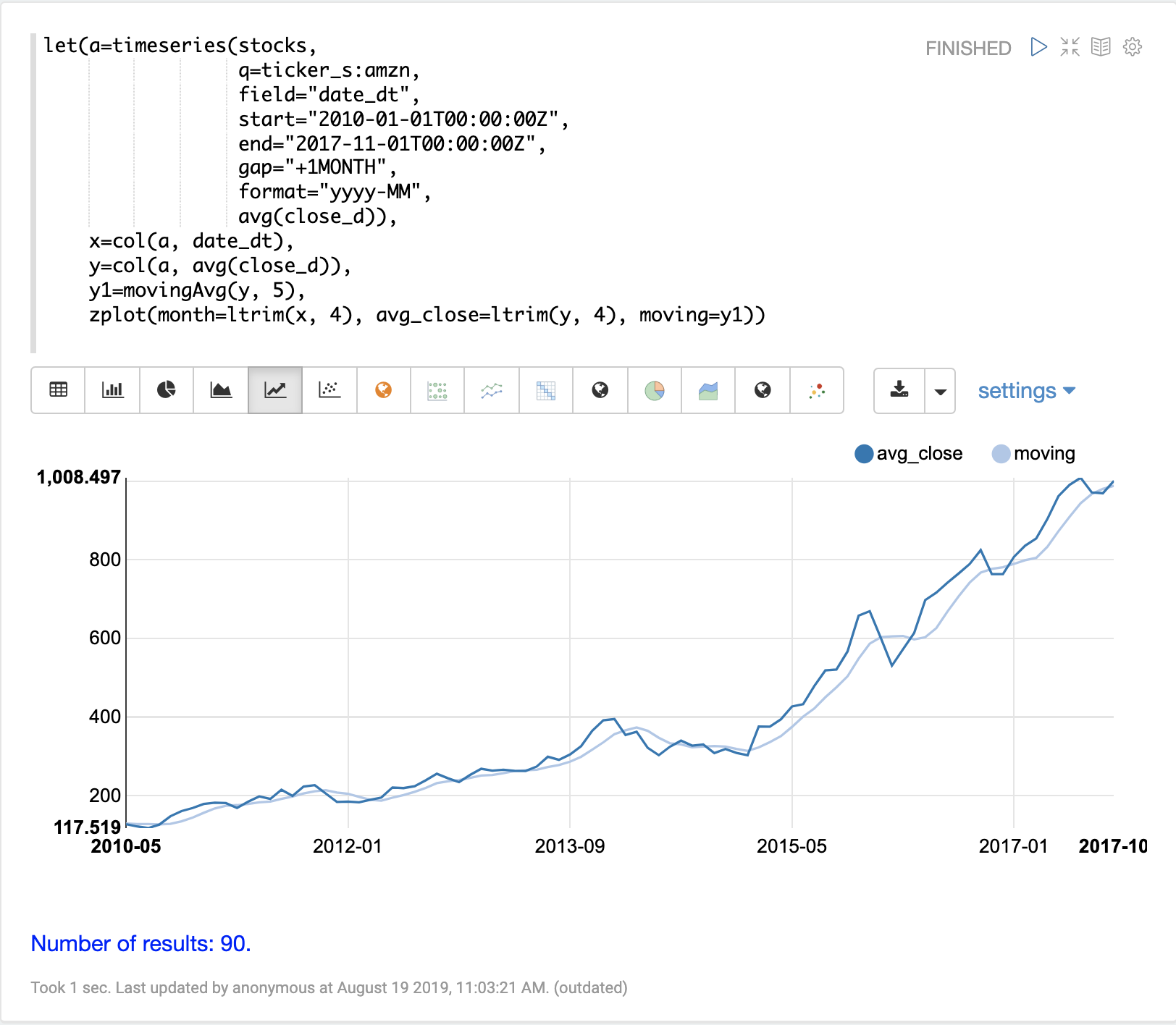
差分
差分は、時系列からトレンドや季節性を除去することで、時系列を定常化するために使用できます。
一次差分
差分で使用される手法は、元の値ではなく、値の差を使用することです。一次差分は、ある値とその直前の値の差を計算します。一次差分は、時系列からトレンドを除去するためによく使用されます。
以下の例では、一次差分を使用して、2つの時系列を定常化し、トレンドの影響を受けずに比較できるようにしています。
この例では、AmazonとGoogleの2つの株の月間平均終値を比較します。以下の画像は、差分を適用する前の両方の時系列をプロットしたものです。
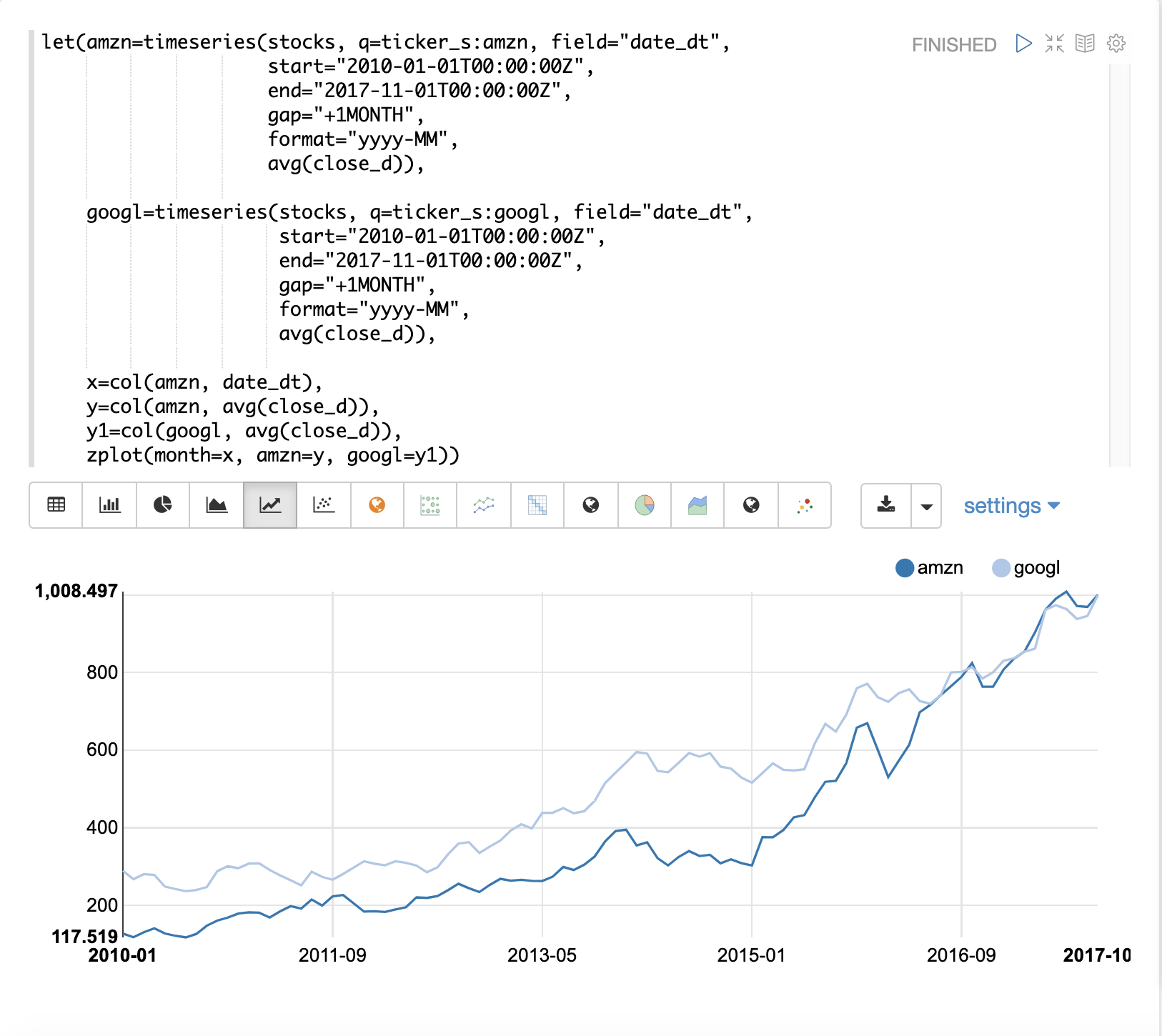
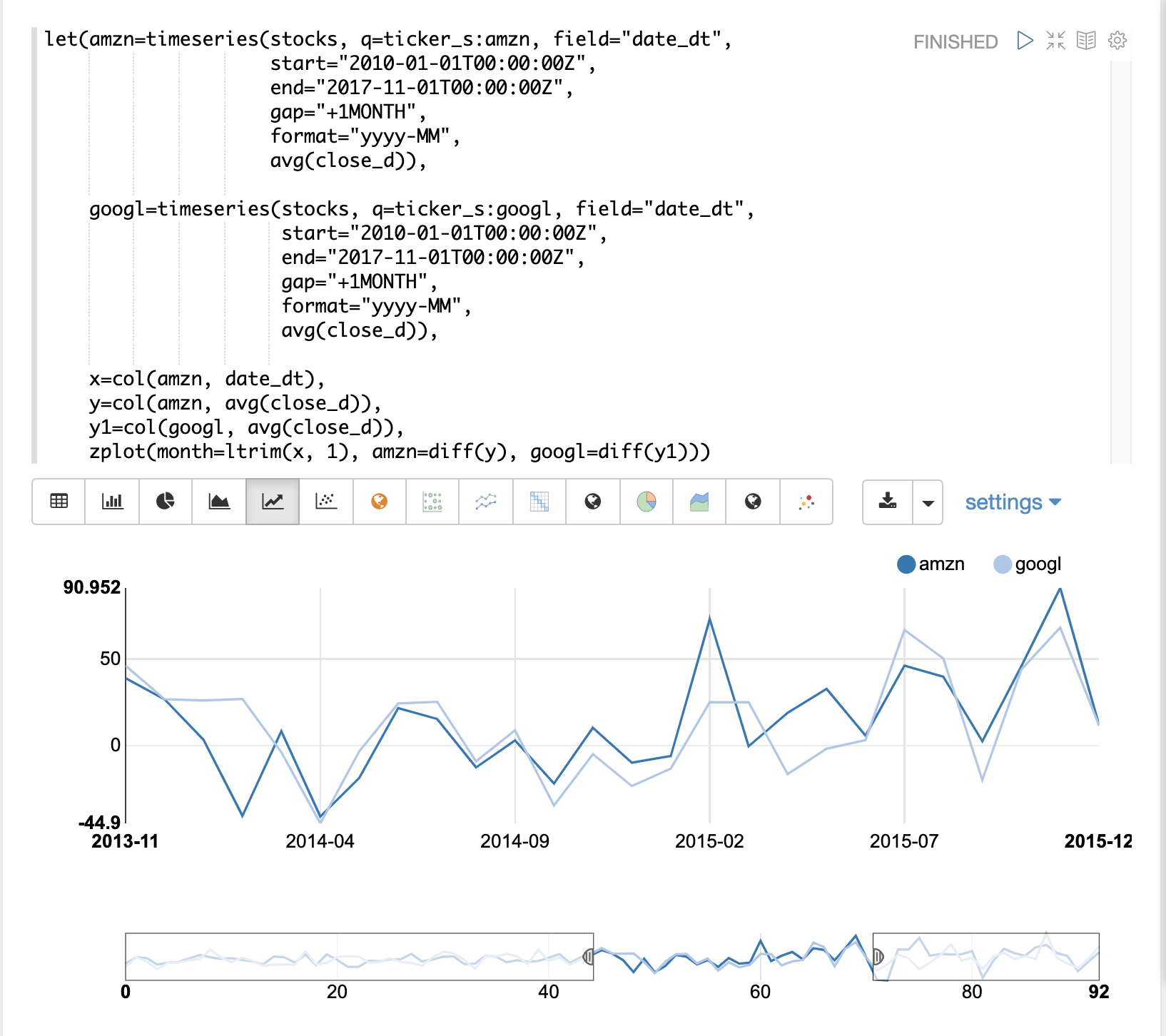
次の例では、zplot関数内で両方の時系列にdiff関数が適用されています。diffは、zplot関数内、またはlet関数内の他の関数と同様に適用できます。
両方の時系列でトレンドが除去され、株価の月ごとの変動がトレンドの影響を受けずに分析できるようになったことに注意してください。
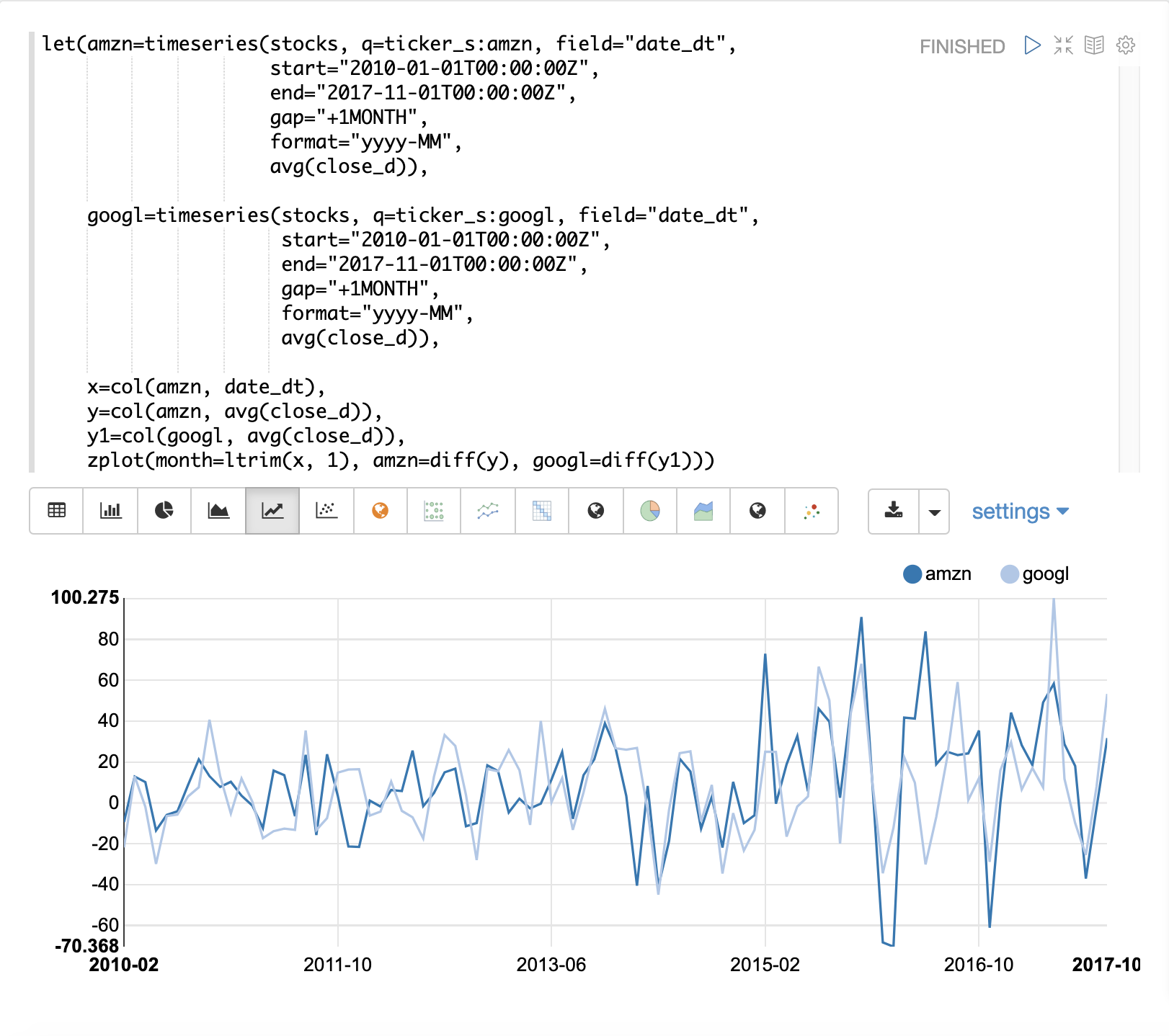
次の例では、時系列可視化のzoom関数を使用して、特定の月の範囲をズームインしています。これにより、データをより詳細に調べることができます。データをより詳細に調べると、2つの株の月ごとの動きの間にある程度の相関関係があるように見えます。
最後の例では、差分処理された時系列をcorr関数で相関させています。
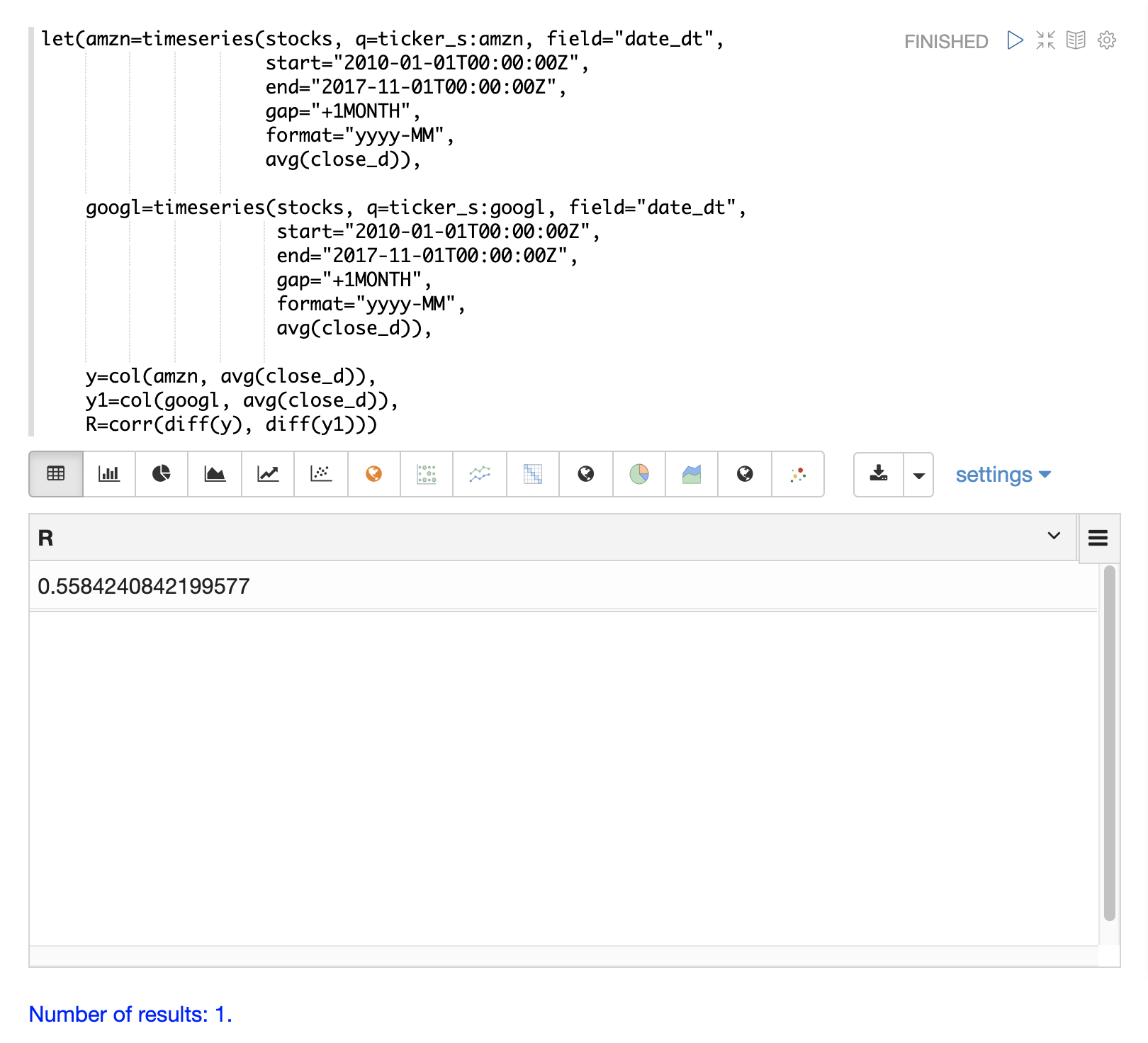
ラグ付き差分
diff関数には、差のラグを指定するためのオプションの2番目のパラメータがあります。ラグが指定された場合、ある値と過去の指定されたラグにある値との差が計算されます。ラグ付き差分は、時系列から季節性を除去するためによく使用されます。
以下の簡単な例は、ラグ付き差分がどのように機能するかを示しています。例の配列が単純な繰り返しパターンに従っていることに注意してください。このタイプのパターンは、季節性とともに表示されることがよくあります。
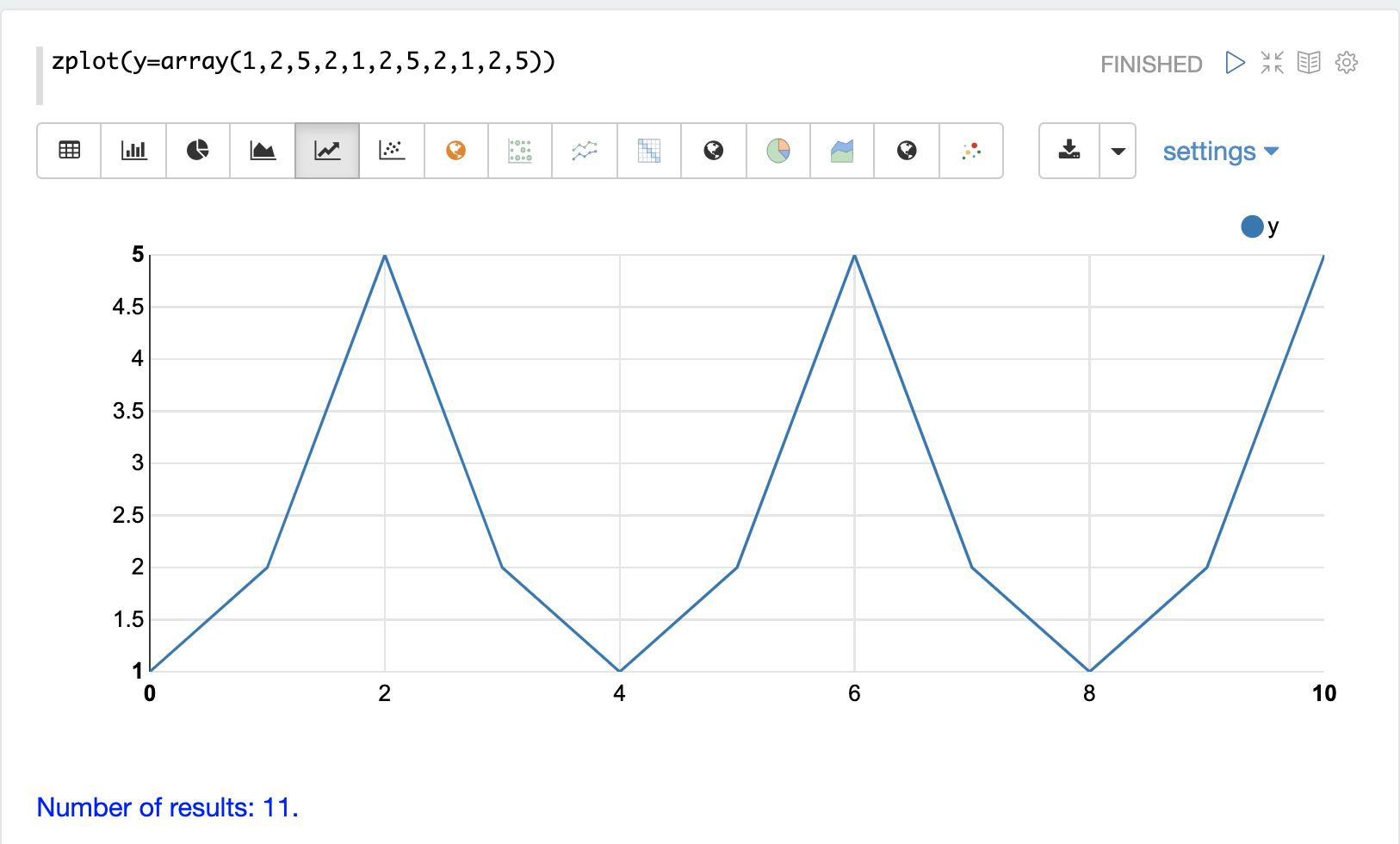
この例では、ラグ4でdiff関数を使用してこのパターンを削除します。これにより、現在のインデックスより4つ遅れている値が減算されます。結果セットのサイズは、元の配列のサイズからラグを引いたものになることに注意してください。これは、diff関数がラグ4の計算が可能な値の結果のみを返すためです。
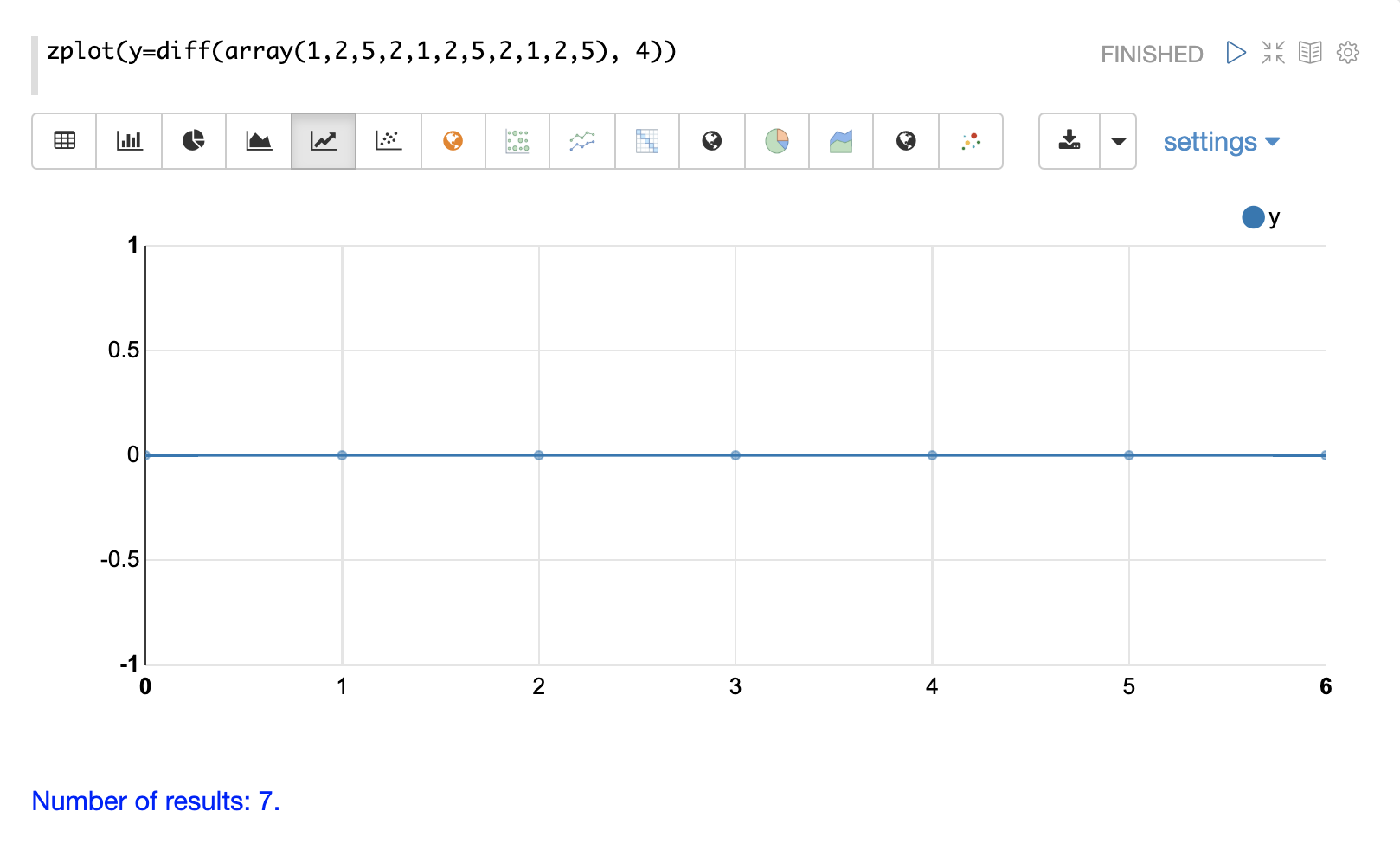
異常検知
movingMAD(移動平均絶対偏差)関数は、スライディングウィンドウ内の分散(平均からの偏差)を測定することにより、時系列の異常を検出するために使用できます。
movingMAD関数は、移動平均と同様の方法で動作しますが、ウィンドウ内の平均ではなく、平均絶対偏差を測定します。異常に高い分散または低い分散を探すことで、時系列の異常を見つけることができます。
この例では、Amazonの2年間の日次株価を使用します。日次株価データは、調査するためのより大きなデータセットを提供します。
以下の例では、search式を使用して、2年間のAMZNのティッカーの日次終値を返します。
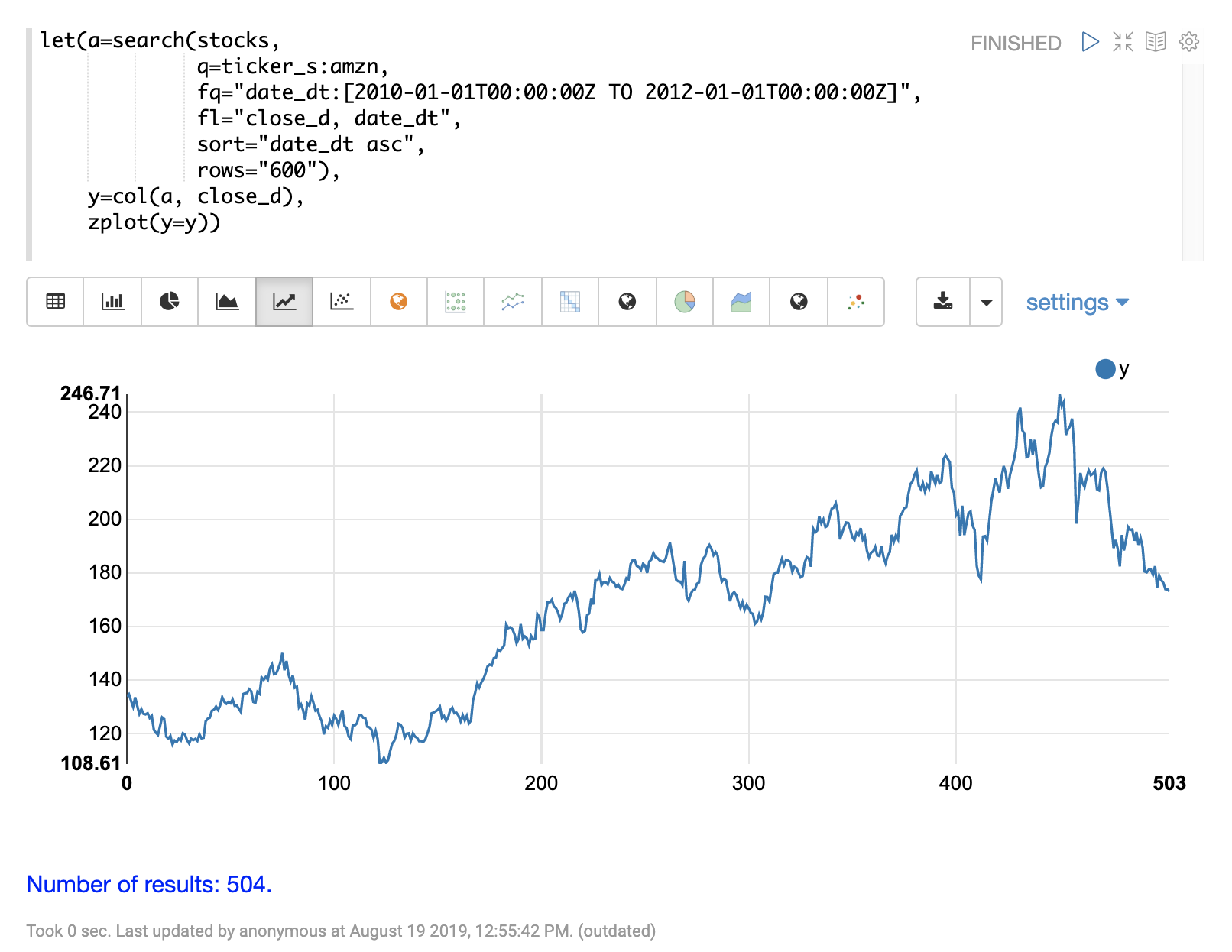
次のステップは、movingMAD関数をデータに適用して、10日間ウィンドウでの移動平均絶対偏差を計算することです。以下の例は、関数が適用され、可視化されている様子を示しています。
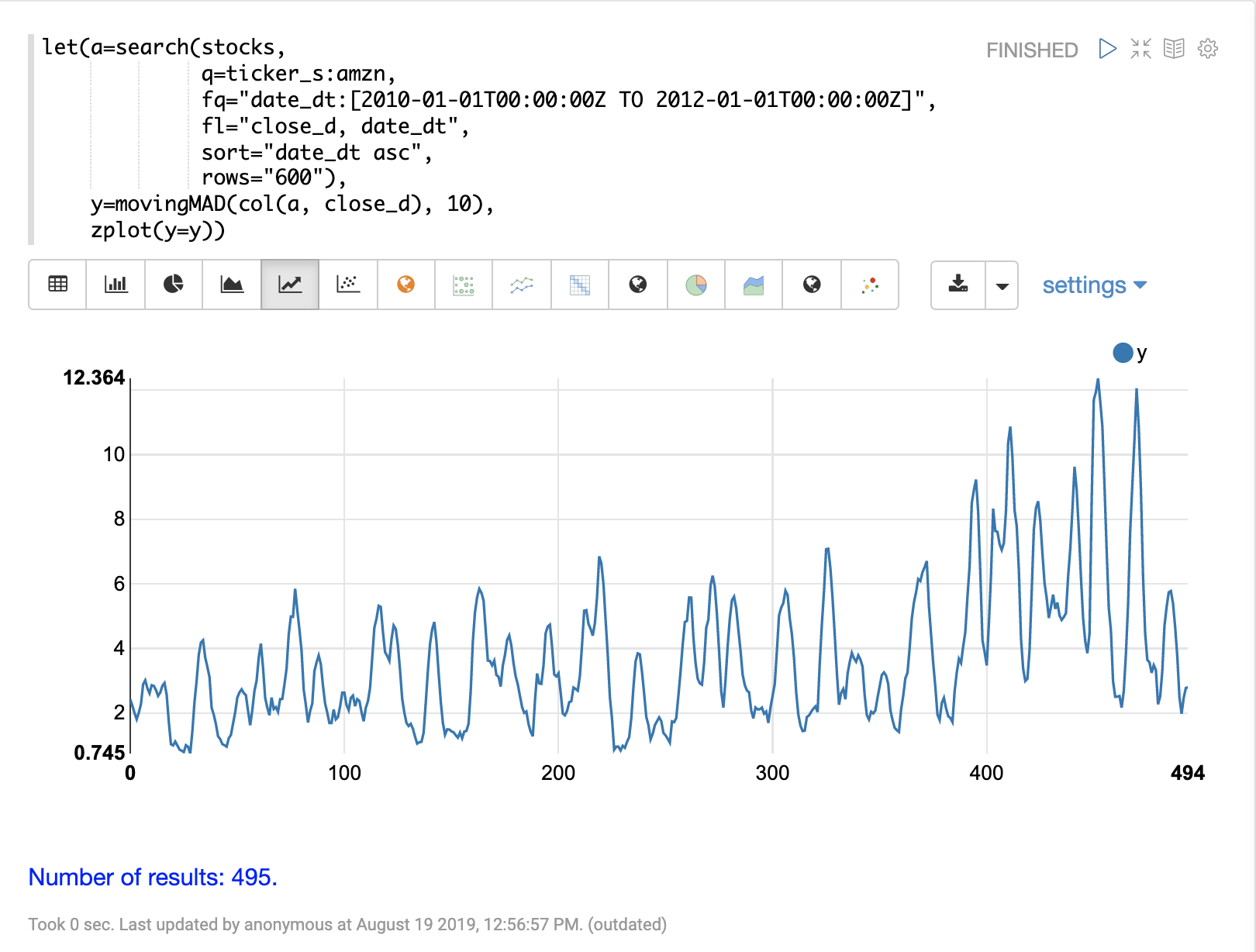
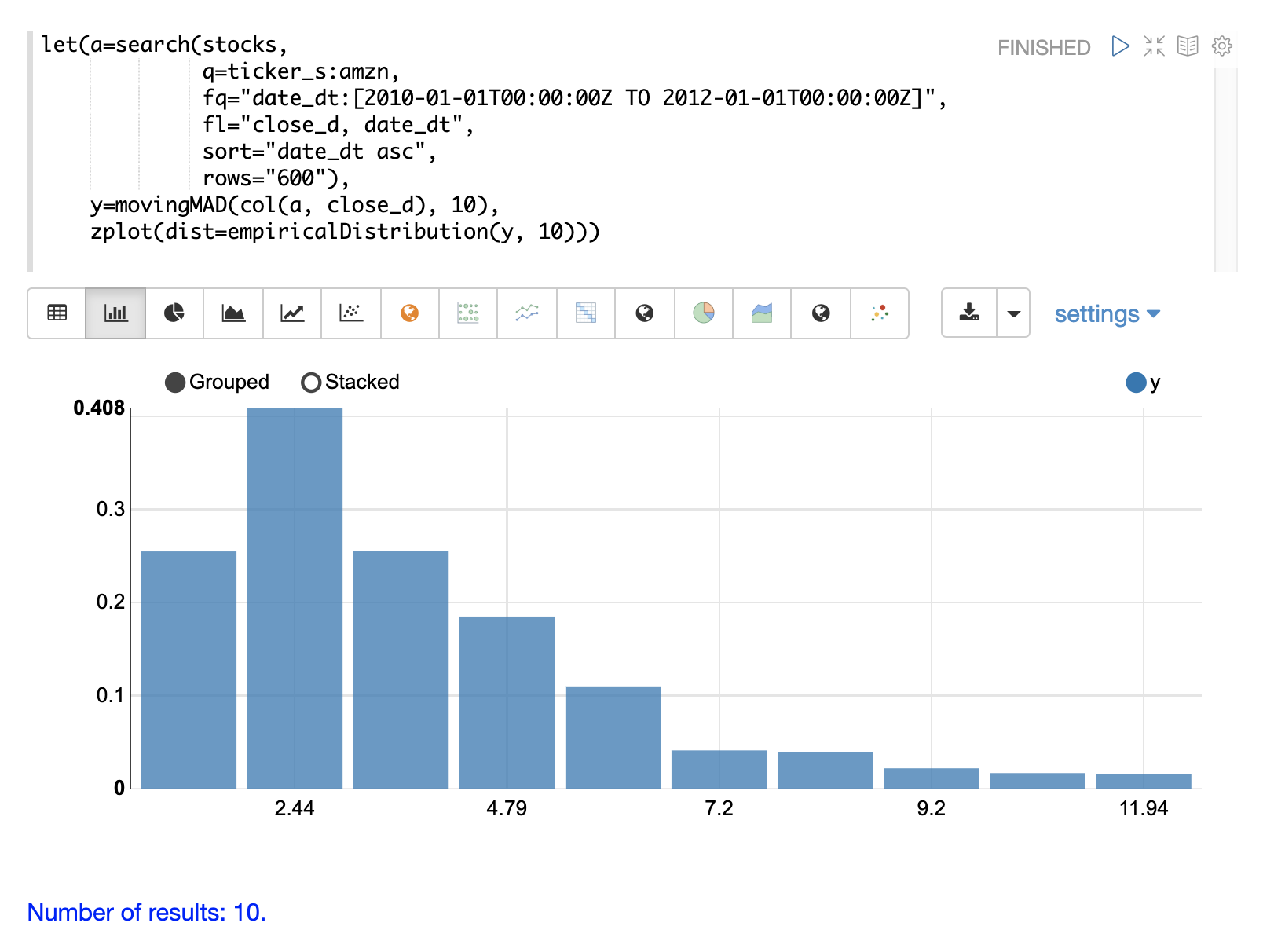
移動MADが計算されたら、empiricalDistribution関数を使用して分散の分布を可視化できます。以下の例では、10個のビンを使用して経験分布をプロットし、時系列の分散の10ビンヒストグラムを作成しています。
この可視化は、平均絶対偏差のほとんどが0から9.2の間であり、最後のビンの平均が11.94であることを示しています。
最後のステップは、outliers関数を使用して系列の外れ値を検出することです。outliers関数は、確率分布を使用して、数値ベクトルの外れ値を検出します。outliers関数は、4つのパラメータを取ります。
-
確率分布
-
数値ベクトル
-
低い確率のしきい値
-
高い確率のしきい値
-
数値ベクトルが選択された結果のリスト
outliers関数は、数値ベクトルを反復処理し、確率分布を使用して各値の累積確率を計算します。累積確率が低い確率しきい値未満または高いしきい値を超えている場合、その値を外れ値と見なします。outliers関数が外れ値を検出すると、5番目のパラメータで提供された結果のリストから対応する結果を返します。また、累積確率と外れ値の値も含まれます。
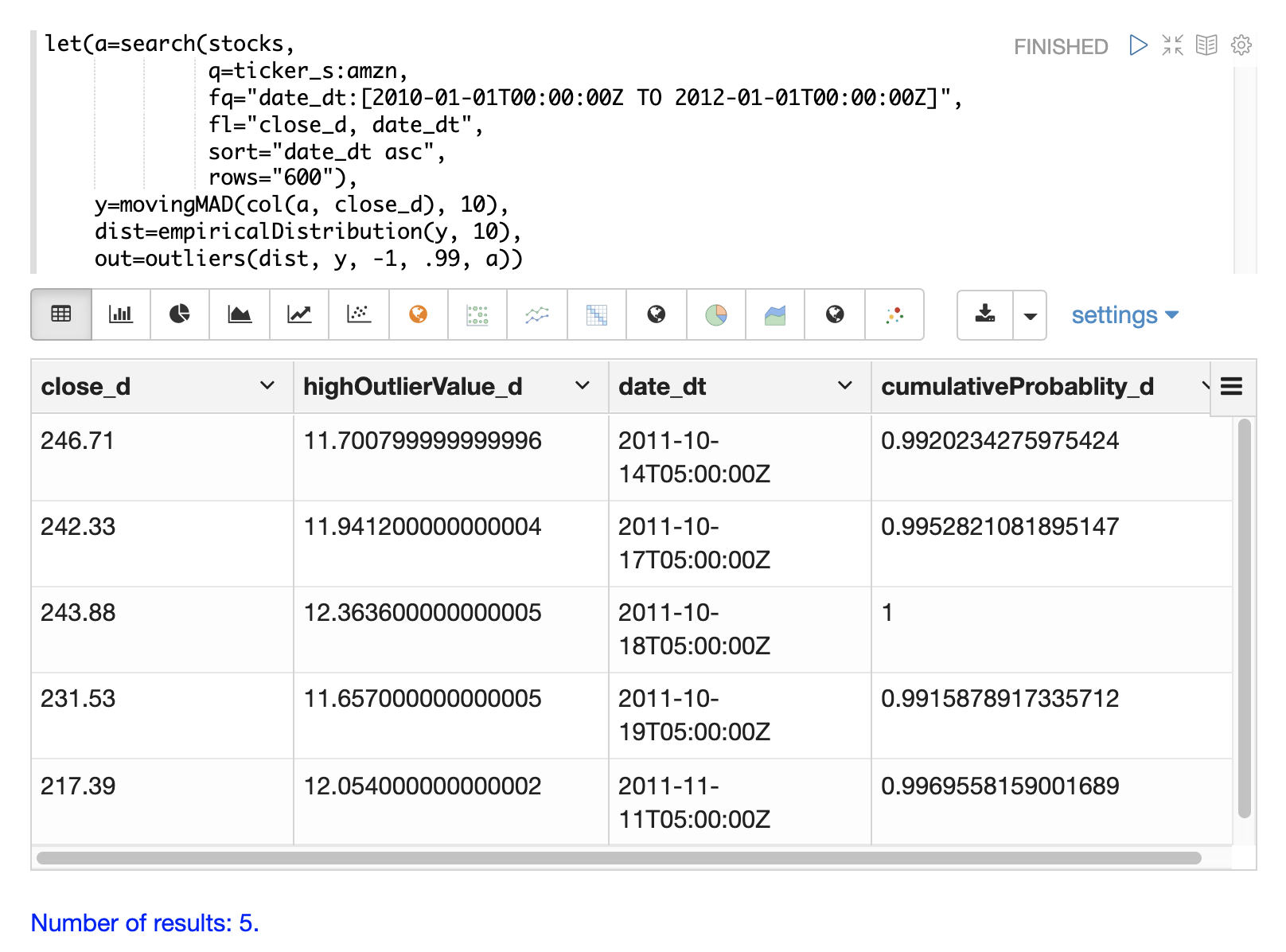
以下の例は、Amazon株価データセットに適用されたoutliers関数を示しています。移動平均絶対偏差の経験分布が最初のパラメータです。移動平均絶対偏差を含むベクトルが2番目のパラメータです。-1は低く、.99は高い確率しきい値です。-1は、低い外れ値は考慮されないことを意味します。最後のパラメータは、close_dフィールドとdate_dtフィールドを含む元の結果セットです。
outliers関数の出力には、外れ値が検出された結果が含まれています。この場合、.99の確率しきい値を超える5つの結果が検出されました。
モデリング
Solrでの数式式のサポートには、時系列のモデル化に使用できる多くの関数が含まれています。これらの関数には、線形回帰、多項式および調和曲線フィッティング、ローエス回帰、およびKNN回帰が含まれます。
これらの各関数は、時系列をモデル化し、補間(データセット内の値を予測)に使用でき、いくつかを使用して外挿(データセットを超えた値を予測)に使用できます。
さまざまな回帰関数については、ユーザーガイドの線形回帰、曲線フィッティング、および機械学習のセクションで詳しく説明しています。
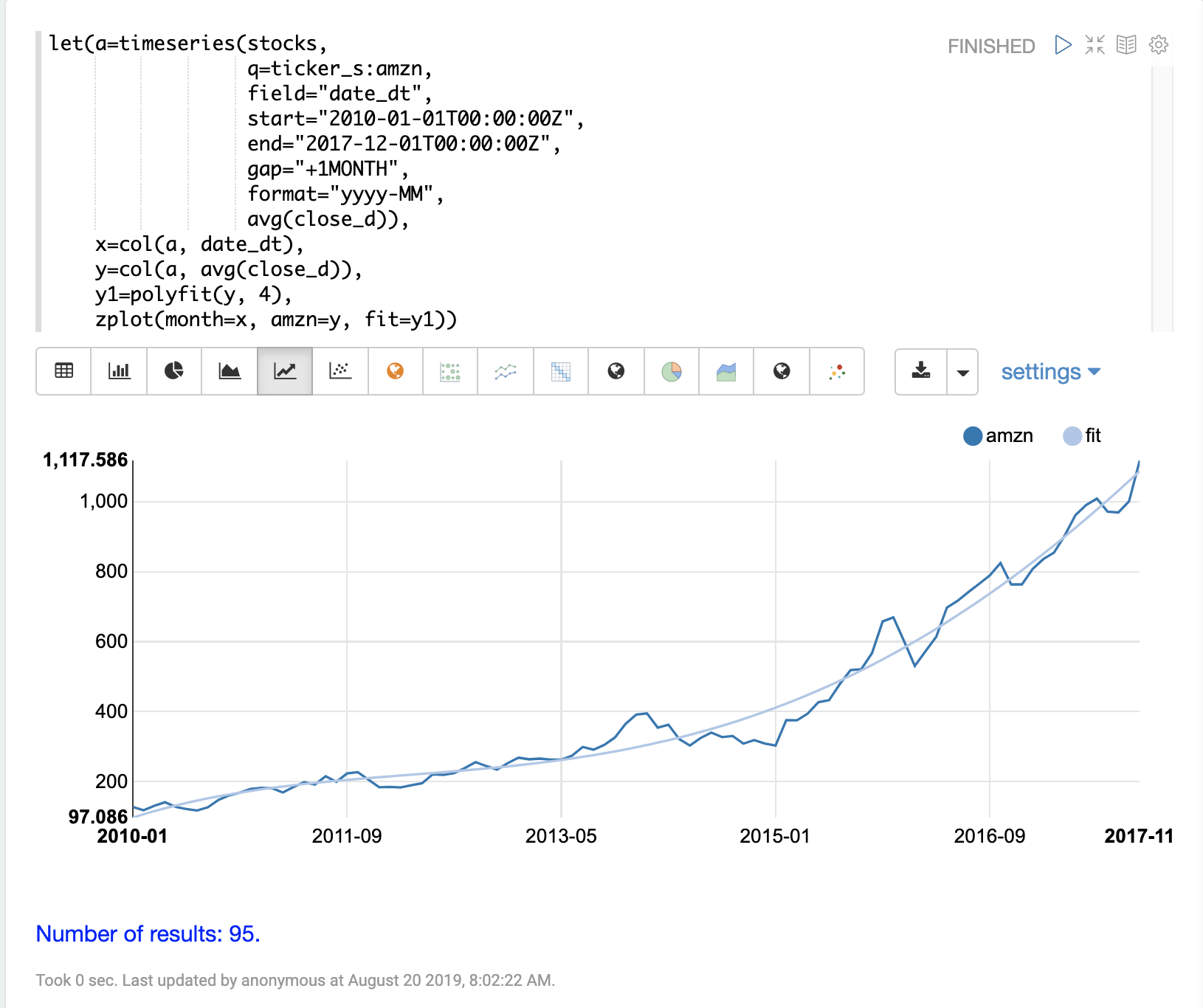
以下の例では、polyfit関数(多項式回帰)を使用して、時系列に非線形モデルを適合させています。使用されているデータセットは、8年間のAmazonの月間平均終値です。
この例では、polyfit関数は、4次多項式を使用して、月間平均終値であるy軸に適合するモデルを返します。多項式の次数によって、モデルの曲線数が決まります。適合したモデルは、変数y1に設定されます。適合したモデルは、元のy値とともにzplotで直接プロットされます。
可視化は、平均終値データに適合する滑らかな線を示しています。
予測
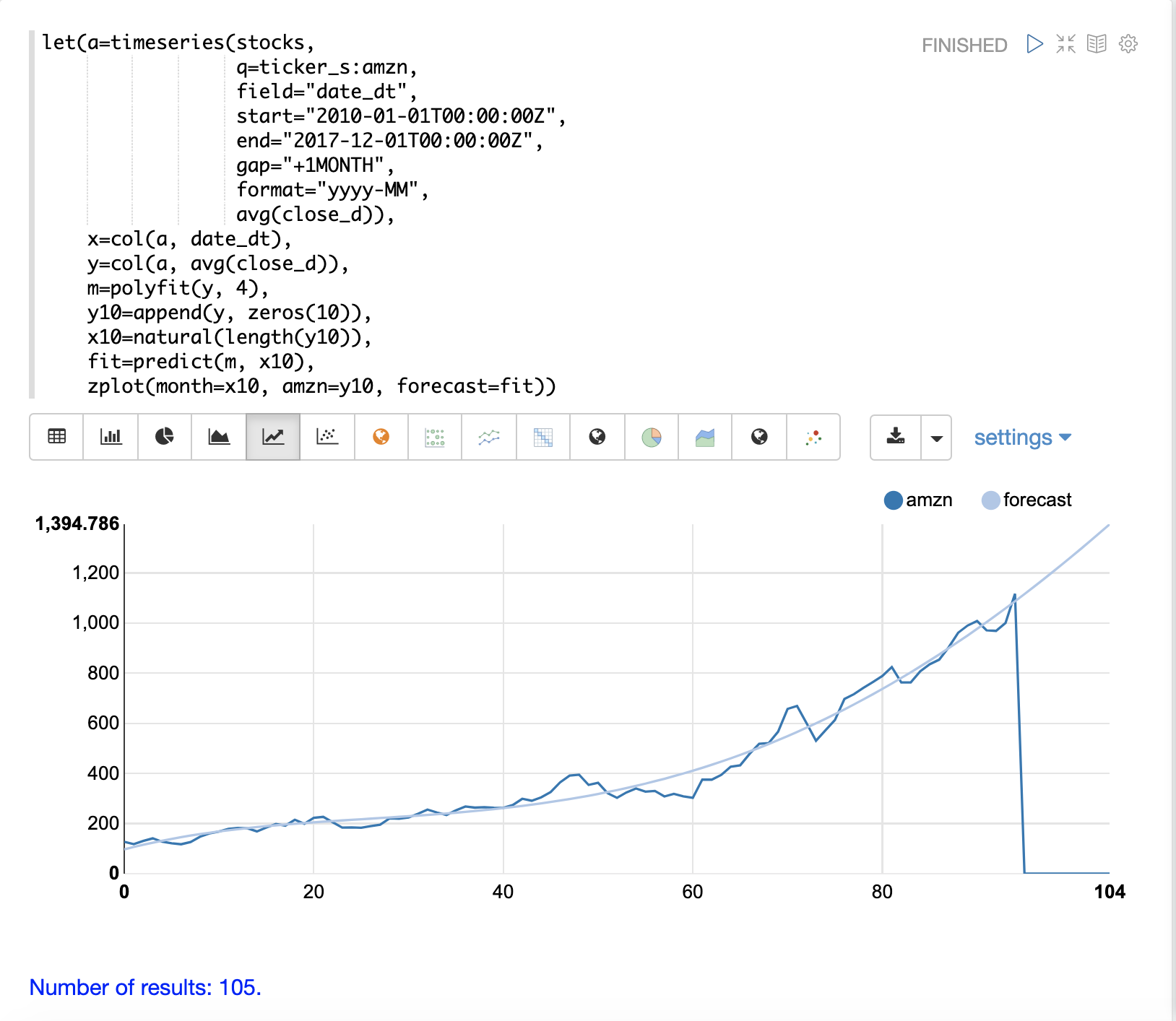
polyfit関数は、時系列を外挿して将来の株価を予測するためにも使用できます。以下の例は、10か月の予測を示しています。
この例では、polyfit関数はy軸にモデルを適合させ、そのモデルは変数mに設定されます。次に、予測を作成するために、10個のゼロがy軸に追加されて、y10という新しいベクトルが作成されます。次に、natural関数を使用して新しいx軸が作成されます。これにより、0からy10の長さまでの整数のシーケンスが返されます。新しいx軸は、変数x10に格納されます。
predict関数は、適合したモデルを使用して、変数x10に格納された新しいx軸の値を予測します。
次に、zplot関数を使用して、x軸にx10ベクトル、y軸にy10ベクトルと外挿モデルをプロットします。y10ベクトルは、観測されたデータが終わるところでゼロになりますが、予測はモデルの適合した曲線に沿って継続することに注意してください。