計算幾何学
数学式のユーザーガイドのこのセクションでは、計算幾何学関数について説明します。
凸包
凸包とは、データセットを囲む最小の凸集合のことです。数学式では、2D データセットの凸包を計算するためのサポートがあります。凸包が計算されると、幾何学的に凸包を記述し、可視化する数学式関数を適用できます。
可視化
convexHull 関数を使用して、一連の 2D 点の周囲に境界線を可視化できます。境界線の可視化は、データ点が境界線に対してどの位置にあるかを理解するのに役立ちます。
以下の例では、convexHull 関数を使用して、NYC311苦情データベースのネズミ目撃情報の緯度と経度の点の集合の境界線を可視化しています。ネズミ目撃情報の周囲の境界線を調査することで、ネズミが特定の地域に出入りする可能性のある方法をより深く理解できます。
散布図
凸包を可視化する前に、2D 点を散布図として可視化することが役立つことがよくあります。
この例では、random 関数を使用して、苦情の説明が「ネズミ目撃情報」と一致し、郵便番号が 11238 である NYC311(苦情データベース)コレクションからレコードのサンプルを描画します。次に、緯度と経度のフィールドをベクトル化し、経度を x 軸、緯度を y 軸として散布図としてプロットします。
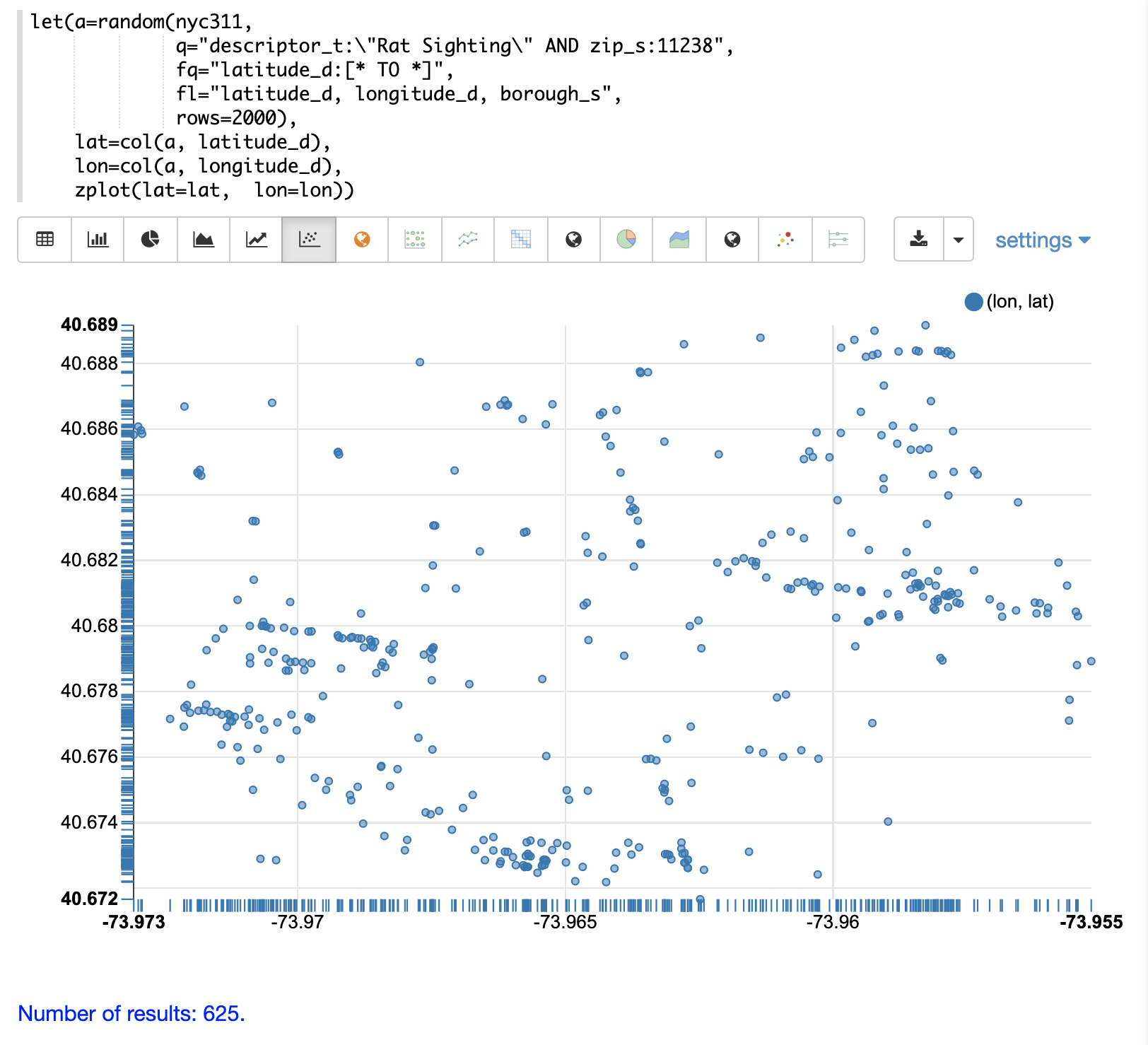
散布図から、多くの点がプロットの境界線付近にあることがわかります。
凸包プロット
convexHull 関数を使用して、境界線を可視化できます。この例では、NYC311 データベースから描画された同じ点を使用します。ただし、点を直接プロットする代わりに、緯度と経度の点をマトリックスに行として追加します。次に、transpose 関数を使用してマトリックスを転置し、マトリックスの各行に単一の緯度と経度の点が含まれるようにします。
次に、convexHull 関数を使用して、点のマトリックスの凸包を計算します。凸包はhullという変数に設定されます。
凸包が作成されると、getVertices 関数を使用して、散布図の凸状の境界線を構成する散布図の点のマトリックスを取得できます。次に、colAt 関数を使用して、マトリックスから緯度と経度のベクトルを取得し、zplot 関数で可視化できるようにします。以下の例では、凸包の点が散布図として可視化されます。
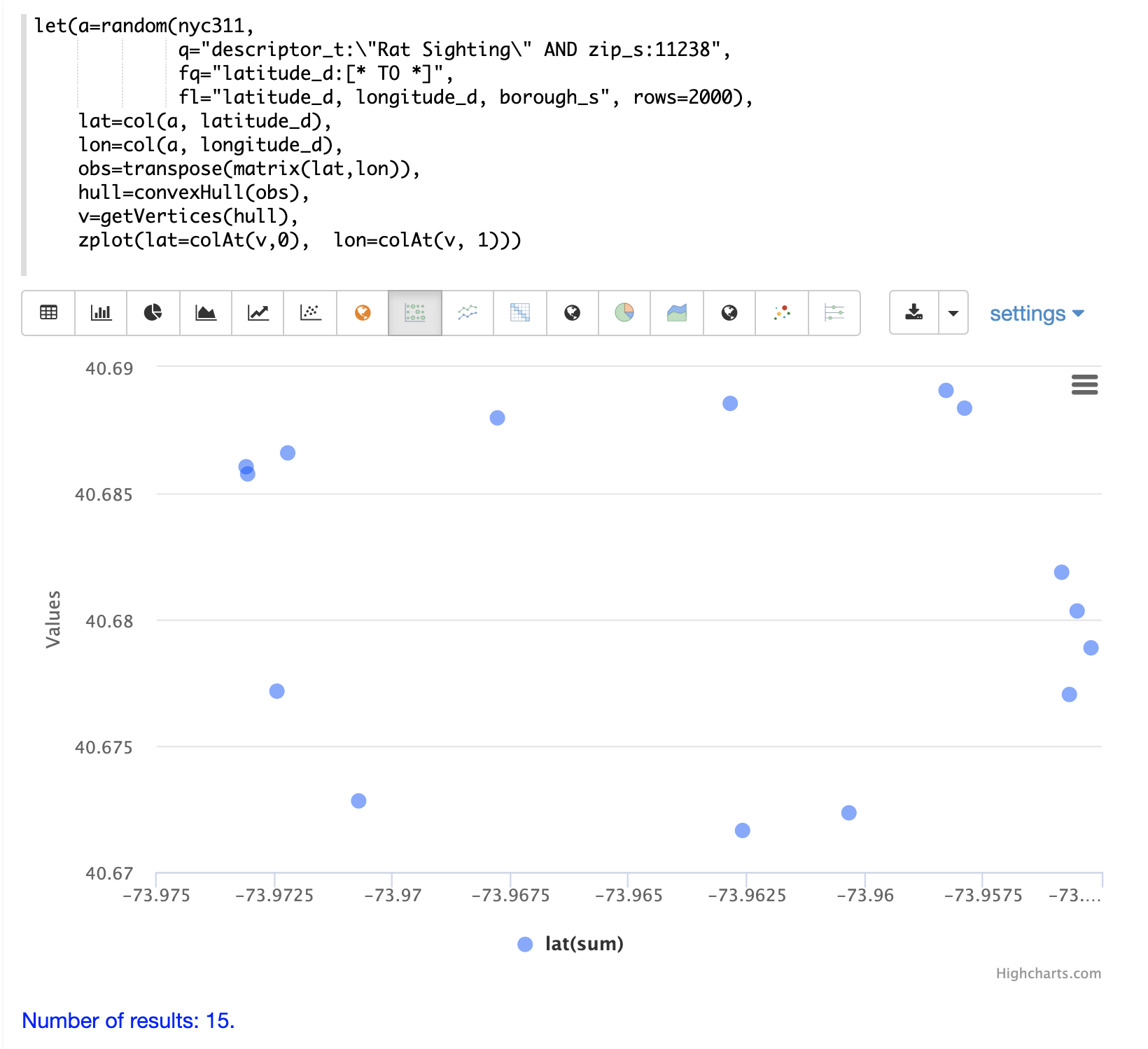
散布図の 15 個の点が、凸包の緯度と経度の点を記述していることに注目してください。
射影とクラスタリング
凸包が計算されると、projectToBorder を使用して、点を境界線上の最も近い点に投影できます。以下の例では、projectToBorder 関数を使用して、元の散布図の点を最も近い境界線に投影しています。
projectToBorder 関数は、境界線の投影の緯度/経度の点のマトリックスを返します。この例では、境界線の点のマトリックスを、kmeans クラスタリングを使用して 7 つのクラスタにクラスタリングします。次に、zplot 関数を使用して、クラスタリングされた境界線をプロットします。
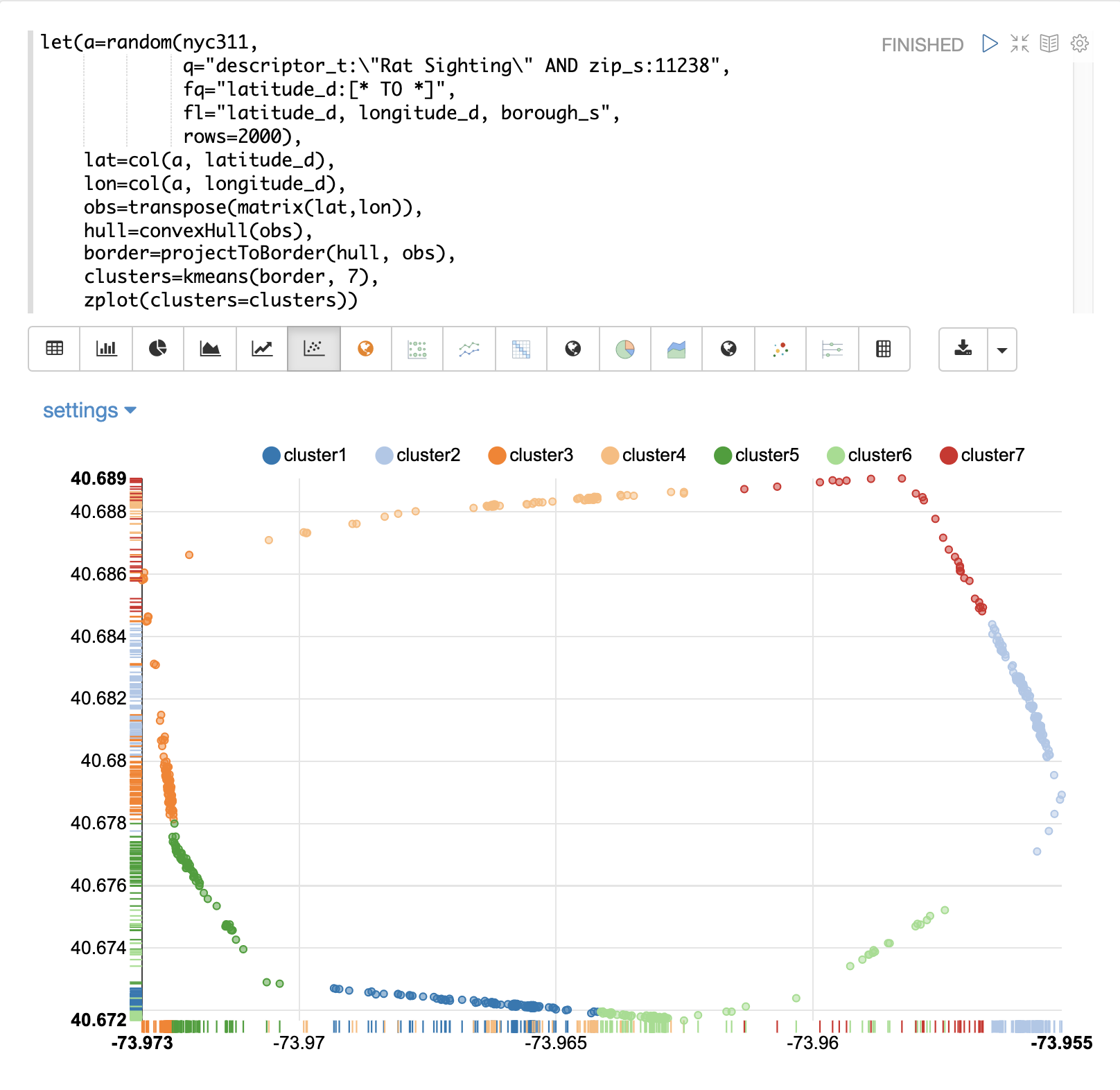
可視化では、境界線のどの点が最も高い密度を持っているかが簡単にわかります。ネズミ目撃情報の場合、この情報は、ネズミが出入りするのに最も近い境界線を理解するのに役立ちます。
セントロイドのプロット
境界線がクラスタリングされると、クラスタのセントロイドを簡単に抽出して地図上にプロットできます。以下の例では、getCentroids 関数を使用してクラスタからセントロイドを抽出します。getCentroids は、境界クラスタのセントロイドを表す緯度/経度の点のマトリックスを返します。次に、colAt 関数を使用して緯度/経度のベクトルを抽出し、zplot を使用して地図上にプロットできます。
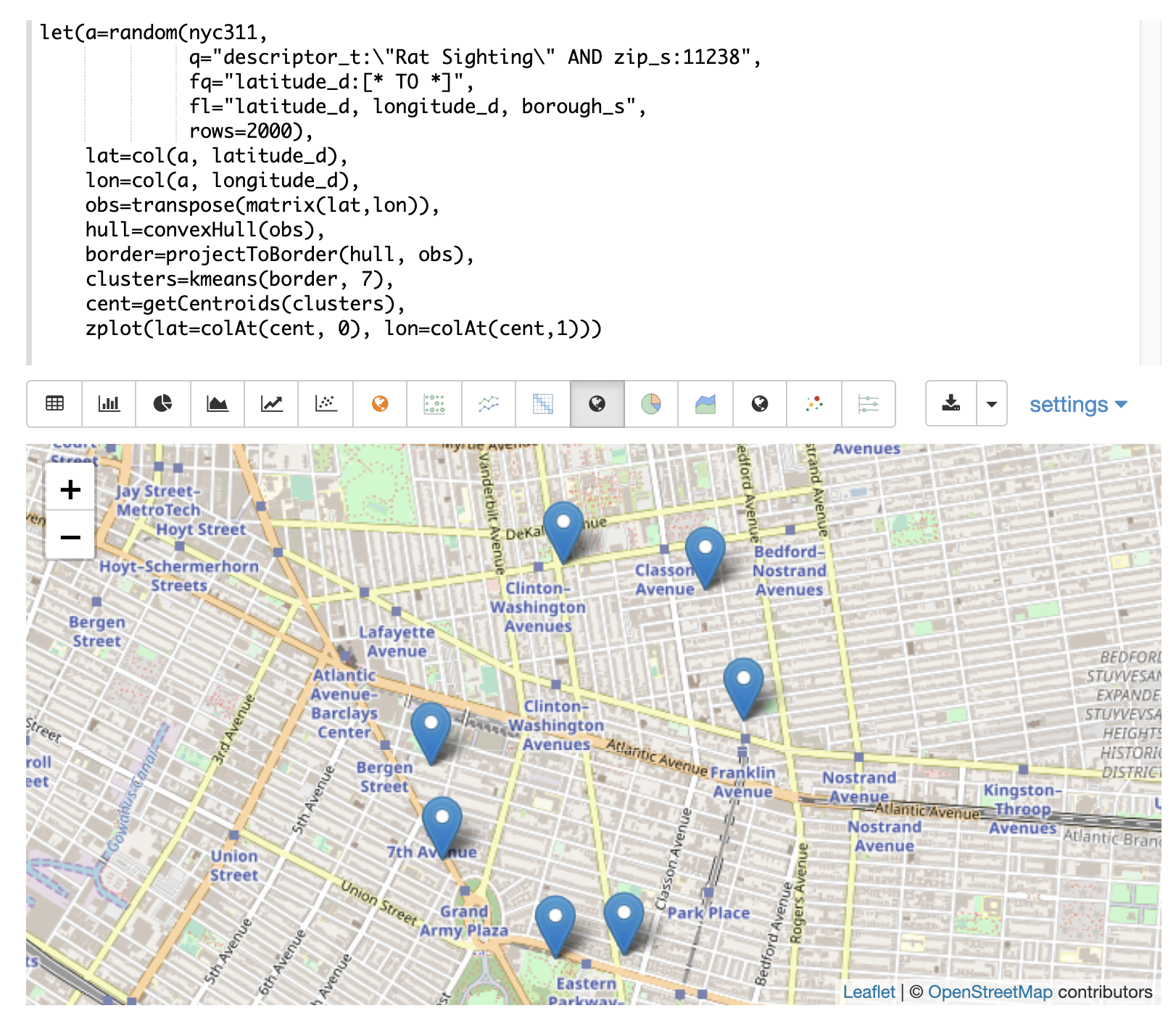
上の地図は、境界クラスタのセントロイドを示しています。最も密度が高いクラスタからのセントロイドは、ズームして地理空間的に調査することで、境界調査を開始するのに最適な場所を判断できます。
最小包含円
enclosingDisk関数は、2Dデータセットを包含する最小の包含円を求めます。包含円が計算されると、一連の数式関数を適用して、包含円を幾何学的に記述できます。
以下の例では、ランダムに生成された1000個の2D観測値のセットに対して、包含円が計算されます。
次に、包含円に対して以下の関数が呼び出されます。
-
getCenter:円の中心となる2D点を返します。 -
getRadius:円の半径を返します。 -
getSupportPoints:円の支持点を返します。
let(echo="center, radius, support",
x=sample(normalDistribution(0, 20), 1000),
y=sample(normalDistribution(0, 20), 1000),
observations=transpose(matrix(x,y)),
disk=enclosingDisk(observations),
center=getCenter(disk),
radius=getRadius(disk),
support=getSupportPoints(disk))この式が/streamハンドラに送信されると、以下のように応答します。
{
"result-set": {
"docs": [
{
"center": [
-6.668825009733749,
-2.9825450908240025
],
"radius": 72.66109546907208,
"support": [
[
20.350992271739464,
64.46791279377014
],
[
33.02079953093981,
57.880978456420365
],
[
-44.7273247899923,
-64.87911518353323
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 8
}
]
}
}