統計
このユーザーガイドのセクションでは、数式で利用できるコア統計関数について説明します。
記述統計
describe 関数は、数値配列の記述統計を返します。describe 関数は、記述統計を含む名前と値のペアを持つ単一の **タプル** を返します。
以下は、**logs** コレクションからドキュメントのランダムサンプルを選択し、結果セット内の response_d フィールドをベクトル化し、describe 関数を使用してベクトルに関する記述統計を返す簡単な例です。
let(a=random(logs, q="*:*", fl="response_d", rows="50000"),
b=col(a, response_d),
c=describe(b))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"sumsq": 36674200601.78738,
"max": 1068.854686837548,
"var": 1957.9752647562789,
"geometricMean": 854.1445499569674,
"sum": 42764648.83319176,
"kurtosis": 0.013189848821424377,
"N": 50000,
"min": 656.023249311864,
"mean": 855.2929766638425,
"popVar": 1957.936105250984,
"skewness": 0.0014560741802307174,
"stdev": 44.24901428005237
},
{
"EOF": true,
"RESPONSE_TIME": 430
}
]
}
}ランダムサンプルには 50,000 レコードが含まれており、応答時間はわずか 430 ミリ秒であることに注意してください。このサイズのサンプルを使用して、非常に大きな基礎となるデータセットの統計を、サブ秒のパフォーマンスで確実に推定できます。
describe 関数は、Zeppelin-Solr を使用してテーブルで視覚化することもできます
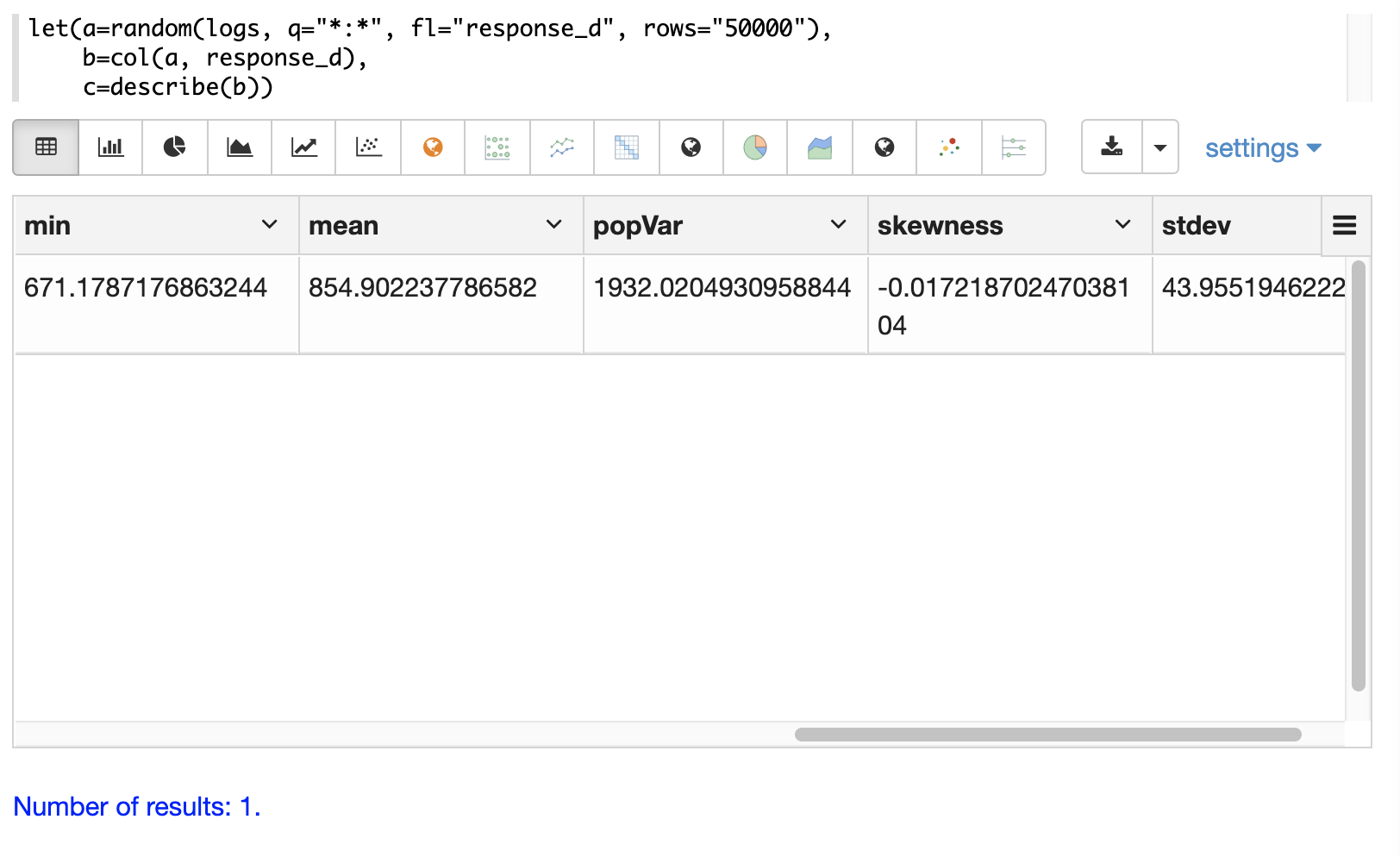
ヒストグラムと度数分布表
ヒストグラムと度数分布表は、確率変数の分布を視覚化するためのツールです。
hist 関数は、連続データでの使用を目的としたヒストグラムを作成します。freqTable 関数は、離散データでの使用を目的とした度数分布表を作成します。
ヒストグラム
以下の例では、ヒストグラムを使用して、ログコレクションからの応答時間のランダムサンプルを視覚化します。この例では、random 関数を使用してランダムサンプルを取得し、結果セットの response_d フィールドからベクトルを作成します。次に、hist 関数をベクトルに適用して、22 個のビンを持つヒストグラムを返します。hist 関数は、各ビンの要約統計を含むタプルのリストを返します。
let(a=random(logs, q="*:*", fl="response_d", rows="50000"),
b=col(a, response_d),
c=hist(b, 22))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"prob": 0.00004896007228311655,
"min": 675.573084576817,
"max": 688.3309631697003,
"mean": 683.805542728906,
"var": 50.9974629924082,
"cumProb": 0.000030022417162809913,
"sum": 2051.416628186718,
"stdev": 7.141250800273591,
"N": 3
},
{
"prob": 0.00029607514624062624,
"min": 696.2875238591652,
"max": 707.9706315779541,
"mean": 702.1110569558929,
"var": 14.136444379466969,
"cumProb": 0.00022705264963879807,
"sum": 11233.776911294284,
"stdev": 3.759846323916307,
"N": 16
},
{
"prob": 0.0011491235433157194,
"min": 709.1574910598678,
"max": 724.9027194369135,
"mean": 717.8554290699951,
"var": 20.6935845290122,
"cumProb": 0.0009858515418689757,
"sum": 41635.61488605971,
"stdev": 4.549020172412098,
"N": 58
},
...
]}}Zeppelin-Solr を使用すると、ヒストグラムを最初にテーブルとして視覚化できます
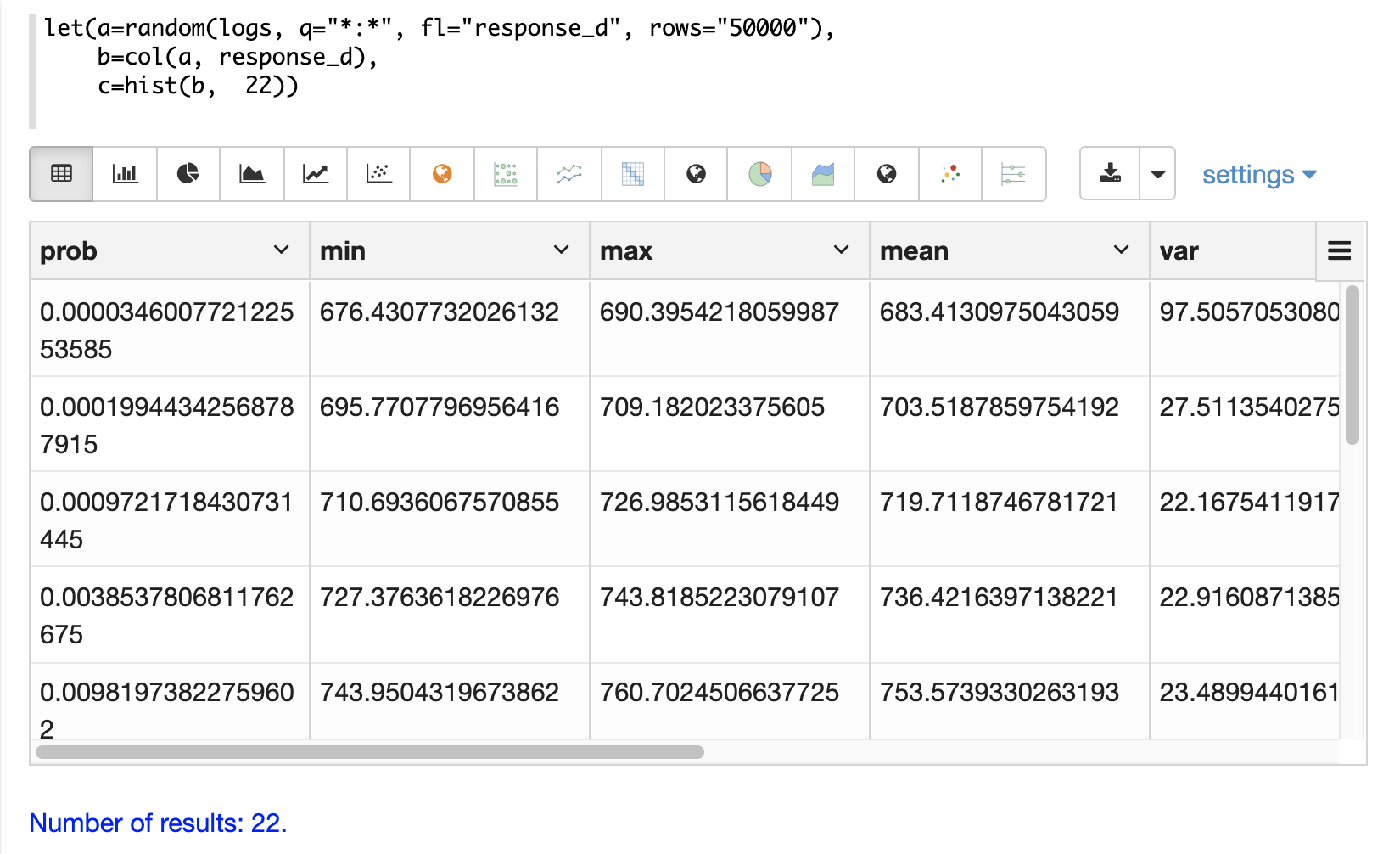
次に、**x軸** にビンの **平均** を、**y軸** に **prob** (確率) をプロットすることで、ヒストグラムを面グラフで視覚化できます
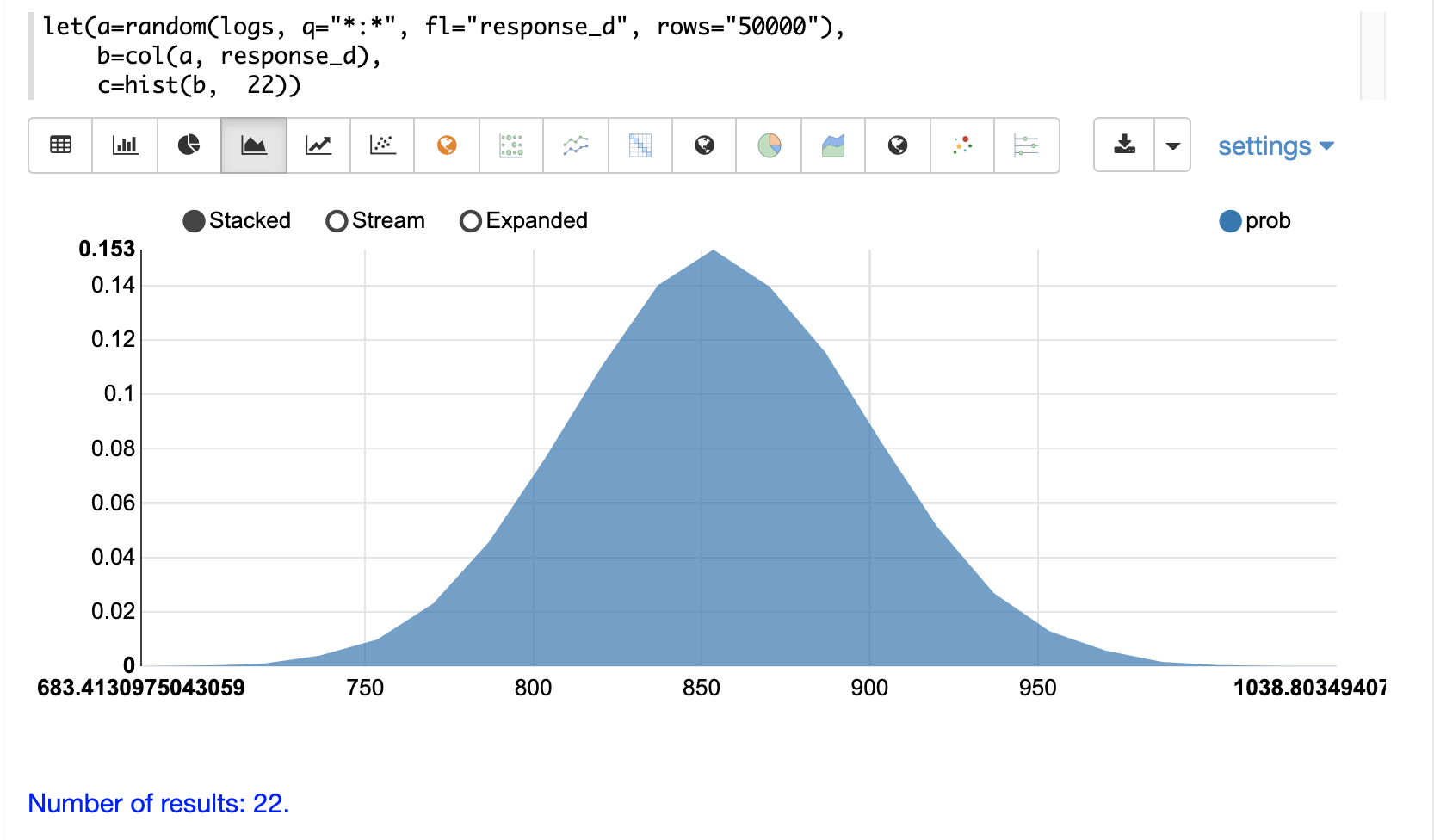
累積確率をプロットするには、**y軸** を **cumProb** 列に切り替えます
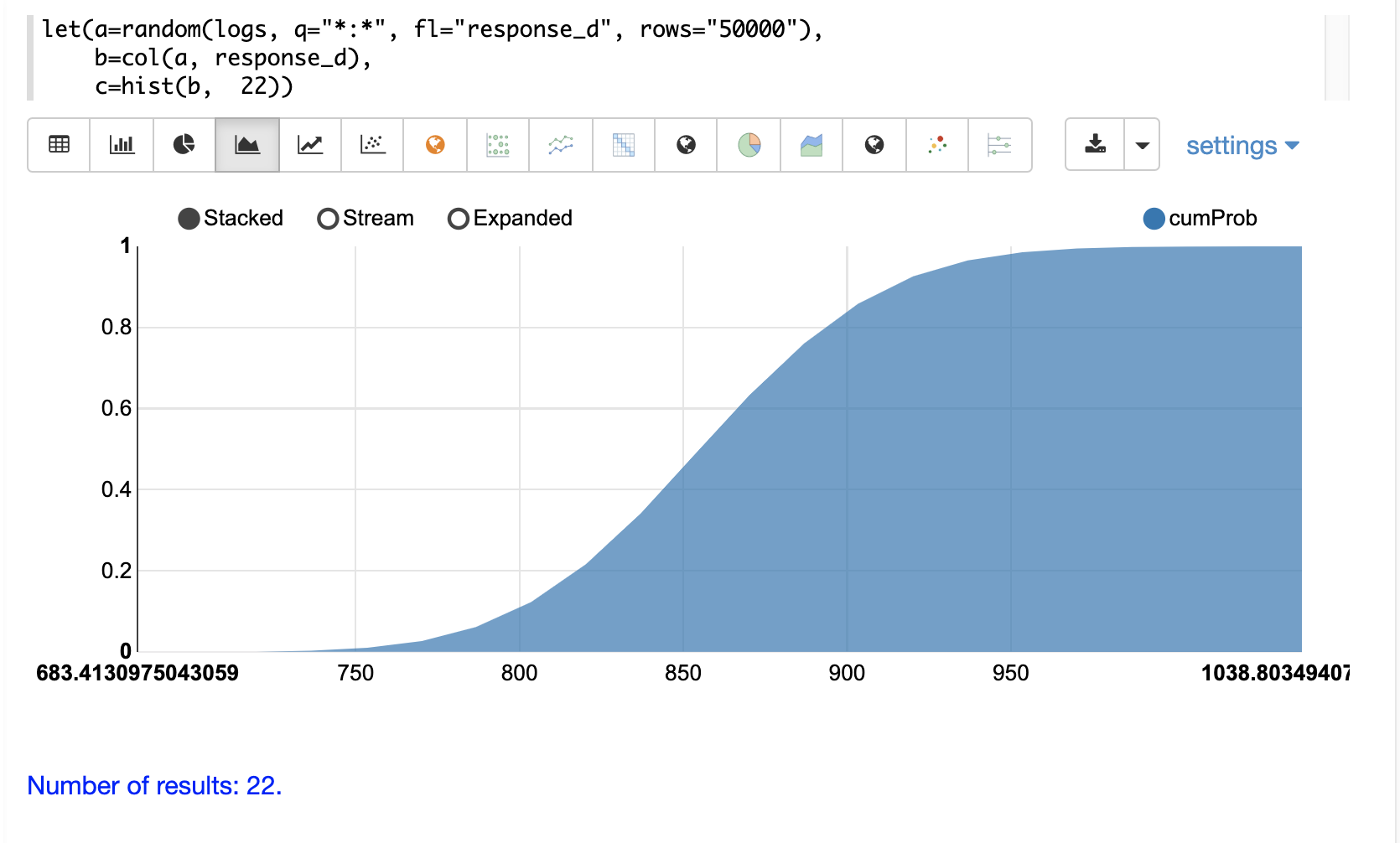
カスタムヒストグラム
複数の stats 関数の出力を組み合わせて、カスタムヒストグラムを定義および視覚化できます。数値フィールドを自動的にビン分割する代わりに、カスタムヒストグラムでは、クエリに基づいてビンを比較できます。
stats 関数については、ユーザーガイドの **検索、サンプリング、集計** セクションで最初に説明します。 |
簡単な例で、カスタムヒストグラムを定義および視覚化する方法を説明します。
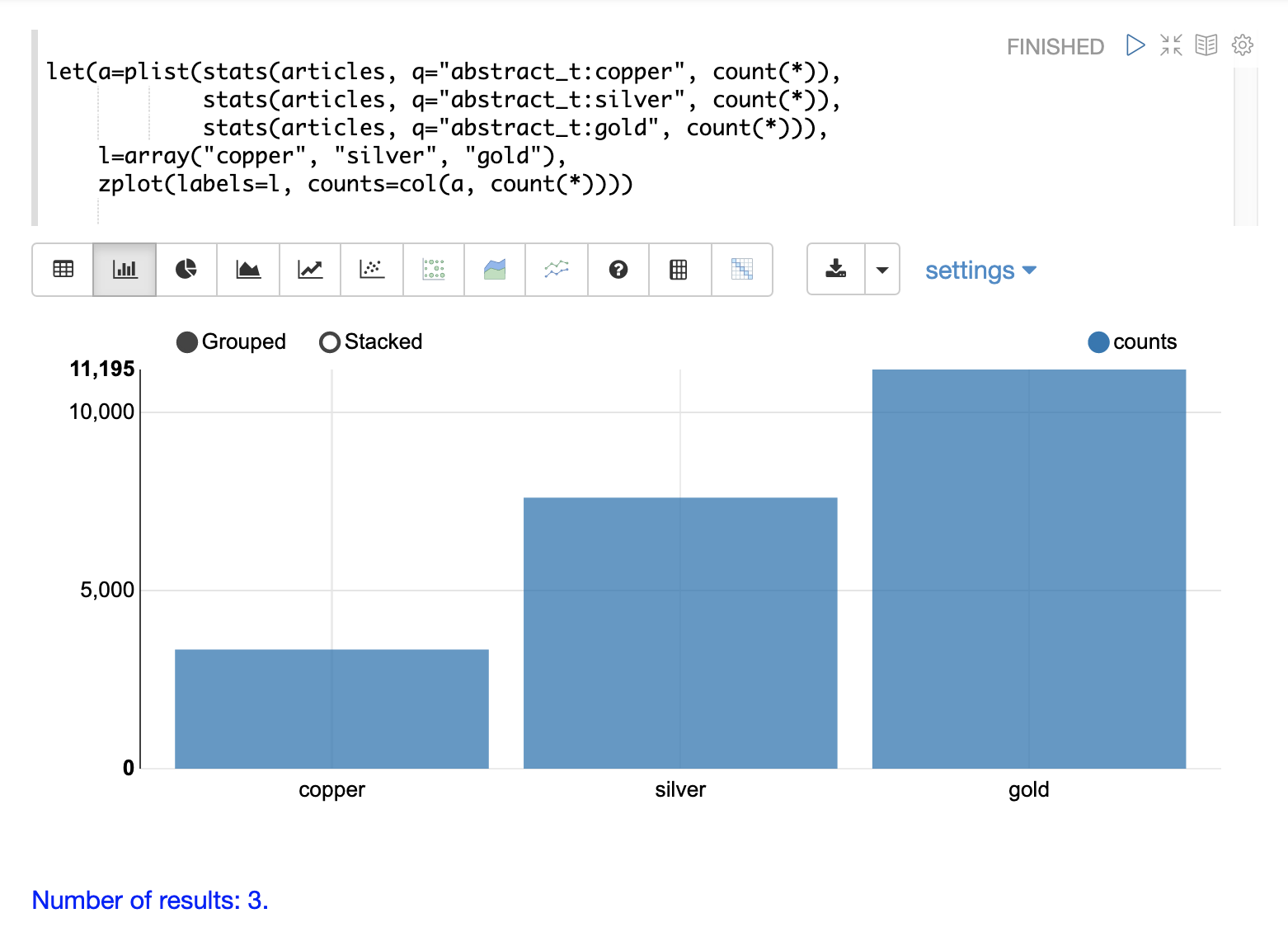
この例では、3つの stats 関数が plist 関数でラップされています。plist (並列リスト) 関数は、内部の各関数を並列で実行し、結果を単一のストリームに連結します。plist は、サブ関数の出力の順序も維持します。この例では、各 stats 関数は特定のクエリに一致するドキュメントの数を計算します。この場合、銅、金、銀の用語を含むドキュメントの数をカウントします。カウントを含むタプルのリストは、変数 **a** に保存されます。
次に、ラベルの array が作成され、変数 **l** に設定されます。
最後に、zplot 関数を使用して、ラベルベクトルと count(*) 列をプロットします。zplot 関数内で col 関数を使用して、stats の結果からカウントを抽出していることに注意してください。
度数分布表
freqTable 関数は、離散データセットの度数分布を返します。freqTable 関数は、ヒストグラムのようにビンを作成しません。代わりに、各離散データの値の出現回数をカウントし、各値の度数統計を含むタプルのリストを返します。
以下は、株価ティッカー **amzn** の日中の始値の丸められた **差** の結果セットから作成された度数分布表の例です。
この例は、結果に至るまでの多段階プロセスを示しているため興味深いです。最初のステップは、stocksコレクション内でティッカーがamznのレコードを検索することです。結果セットは日付昇順でソートされ、その日の始値であるopen_dフィールドを返すことに注意してください。
次に、open_dフィールドはベクトル化され、変数bに設定されます。これにより、日付昇順で並べられた始値のベクトルが格納されます。
次に、diff関数を使用して、始値ベクトルの1階差分を計算します。1階差分は、単に配列内の各値から前の値を引きます。これにより、1日の価格変動を示す日ごとの価格差の配列が生成されます。
次に、round関数を使用して、価格差を最も近い整数に丸め、離散値のベクトルを作成します。この例のround関数は、連続データを整数の境界で効果的にビン分割しています。
最後に、離散値に対してfreqTable関数が実行され、頻度表が計算されます。
let(a=search(stocks,
q="ticker_s:amzn",
fl="open_d, date_dt",
sort="date_dt asc",
rows=25000),
b=col(a, open_d),
c=diff(b),
d=round(c),
e=freqTable(d))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"pct": 0.00019409937888198756,
"count": 1,
"cumFreq": 1,
"cumPct": 0.00019409937888198756,
"value": -57
},
{
"pct": 0.00019409937888198756,
"count": 1,
"cumFreq": 2,
"cumPct": 0.00038819875776397513,
"value": -51
},
{
"pct": 0.00019409937888198756,
"count": 1,
"cumFreq": 3,
"cumPct": 0.0005822981366459627,
"value": -49
},
...
]}}Zeppelin-Solrを使用すると、頻度表を最初にテーブルとして視覚化できます。
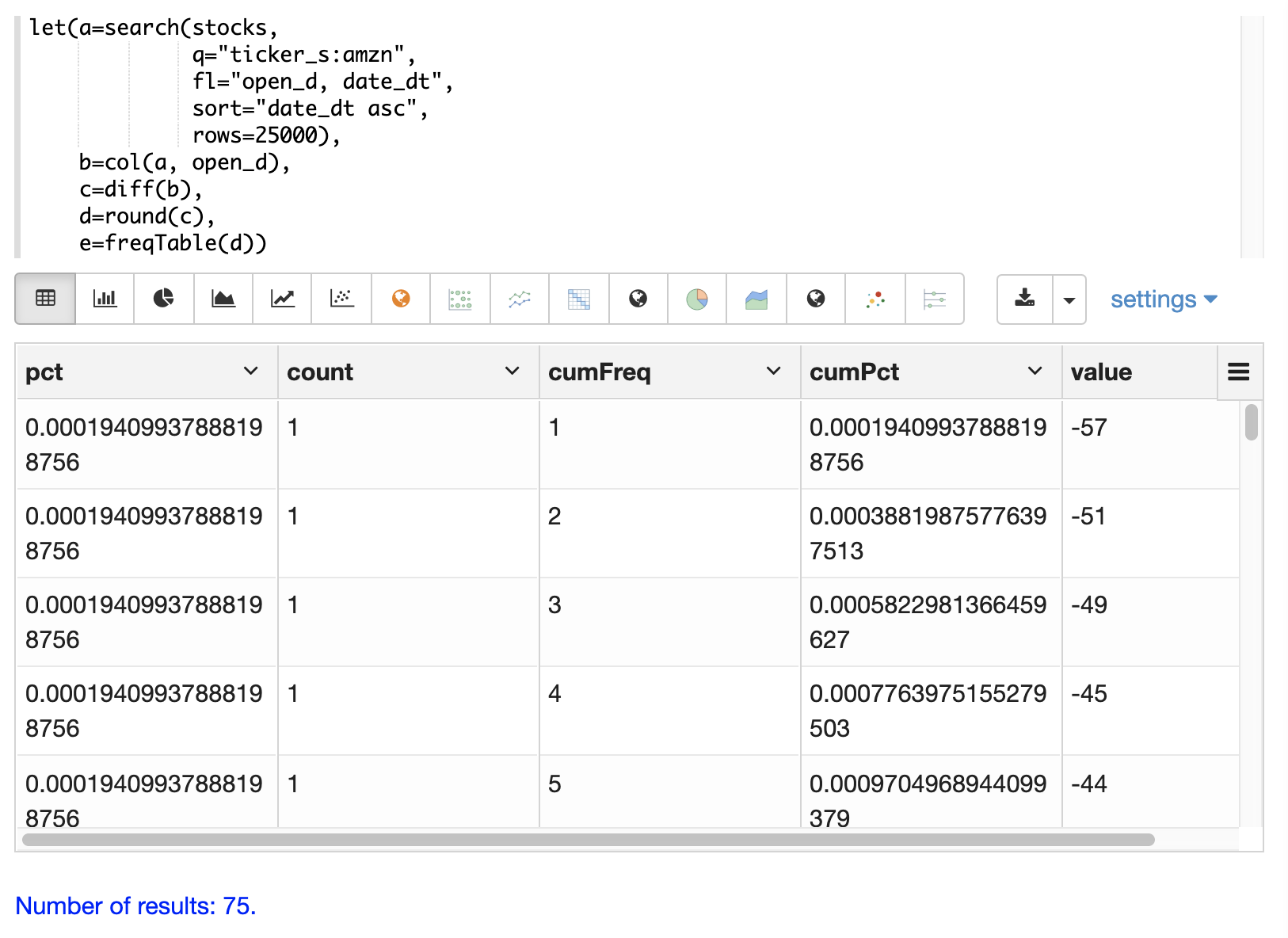
次に、散布図に切り替え、x軸にvalue列、y軸にcount列を選択することで、頻度表をプロットできます。
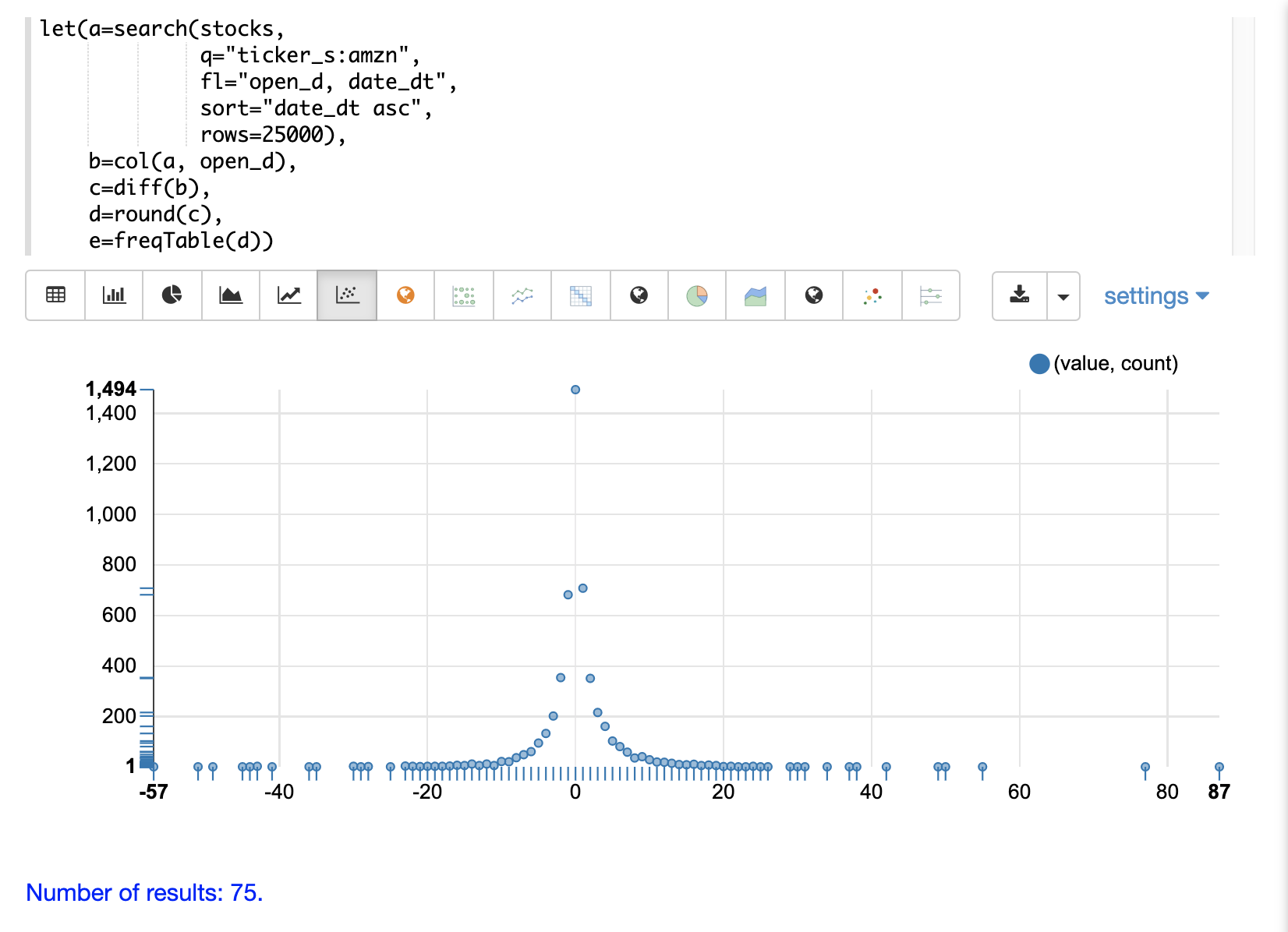
株価の日次変動を整数に丸めた頻度が視覚的にきれいに表示されることに注意してください。最も頻繁に発生する値は0で1494回、次いで-1と1が約700回発生しています。
パーセンタイル
percentile関数は、サンプルセット内の特定のパーセンタイルの推定値を返します。以下の例では、ログコレクションからresponse_dフィールドを含むランダムサンプルを返します。response_dフィールドはベクトル化され、そのベクトルの20パーセンタイルが計算されます。
let(a=random(logs, q="*:*", rows="15000", fl="response_d"),
b=col(a, response_d),
c=percentile(b, 20))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"c": 818.073554
},
{
"EOF": true,
"RESPONSE_TIME": 286
}
]
}
}percentile関数は、パーセンタイル値の配列を計算することもできます。以下の例では、response_dフィールドのランダムサンプルに対して、20、40、60、80パーセンタイルを計算しています。
let(a=random(logs, q="*:*", rows="15000", fl="response_d"),
b=col(a, response_d),
c=percentile(b, array(20,40,60,80)))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"c": [
818.0835543394625,
843.5590348165282,
866.1789509894824,
892.5033386599067
]
},
{
"EOF": true,
"RESPONSE_TIME": 291
}
]
}
}分位点プロット
分位点プロットまたはQQプロットは、2つ以上の分布を視覚的に比較するための強力なツールです。
分位点プロットは、2つ以上の分布のパーセンタイルを同じ視覚化でプロットします。これにより、各パーセンタイルでの分布の視覚的な比較が可能になります。簡単な例で、分位点プロットの威力を説明します。
この例では、2つの株式ティッカー、googとamznの日次株価変動の分布が分位点プロットで視覚化されています。
この例では、最初に計算されるパーセンタイルを表す値の配列を作成し、この配列を変数pに設定します。次に、ティッカーamznとgoogのchange_dフィールドのランダムサンプルが抽出されます。change_dフィールドは、1日あたりの株価変動を表します。次に、change_dフィールドは両方のサンプルに対してベクトル化され、変数amznとgoogに格納されます。次に、percentile関数を使用して、両方のベクトルのパーセンタイルを計算します。計算されるパーセンタイルのリストを指定するために変数pが使用されていることに注意してください。
最後に、zplotを使用して、x軸にパーセンタイルのシーケンス、y軸に計算された両方の分布のパーセンタイル値をプロットします。そして、QQプロットを視覚化するために折れ線グラフが使用されます。
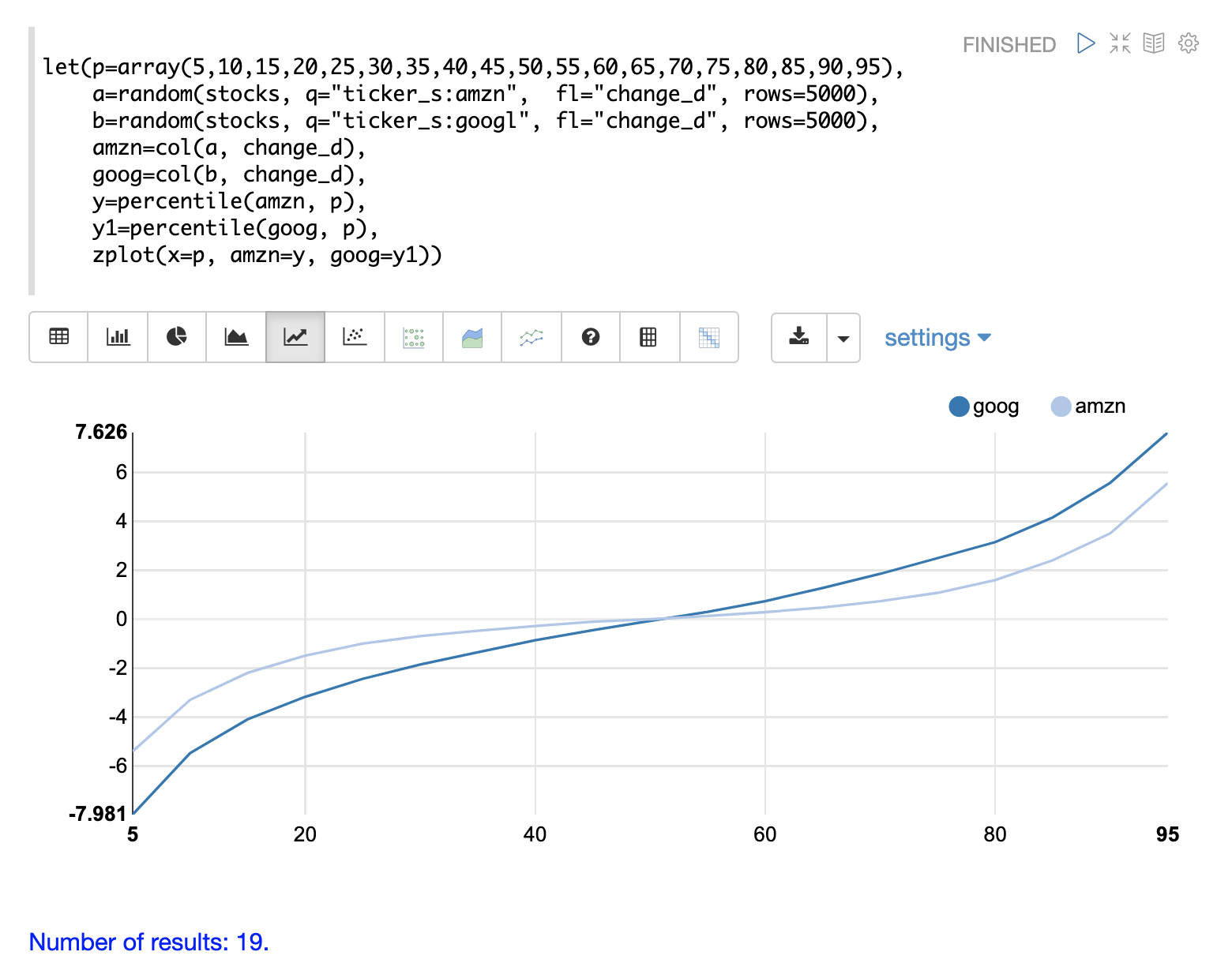
この分位点プロットは、amznとgooglの日次価格変動の分布を明確に示しています。プロットでは、x軸はパーセンタイルであり、y軸は計算されたパーセンタイル値です。
googのパーセンタイル値はamznのプロットよりも低く始まり高く終わっており、勾配がより急であることに注意してください。これは、googの価格変動分布における変動性が大きいことを示しています。このプロットは、パーセンタイルの全範囲にわたる分布の違いを明確に示しています。
相関と共分散
相関と共分散は、ランダム変数がどのように一緒に変動するかを測定します。
相関と相関行列
相関は、2つのベクトルの間の線形相関の尺度です。相関は-1から1の間でスケールされます。
3つの相関タイプがサポートされています。
-
ピアソン(デフォルト)
-
ケンドール
-
スピアマン
相関の種類は、関数呼び出しでtypeという名前付きパラメータを追加することで指定されます。
以下の例では、random関数を使用してログコレクションから2つのフィールド(filesize_dとresponse_d)を含むランダムサンプルが抽出されます。フィールドは変数xとyにベクトル化され、次にcorr関数を使用して2つのベクトルのスピアマンの相関が計算されます。
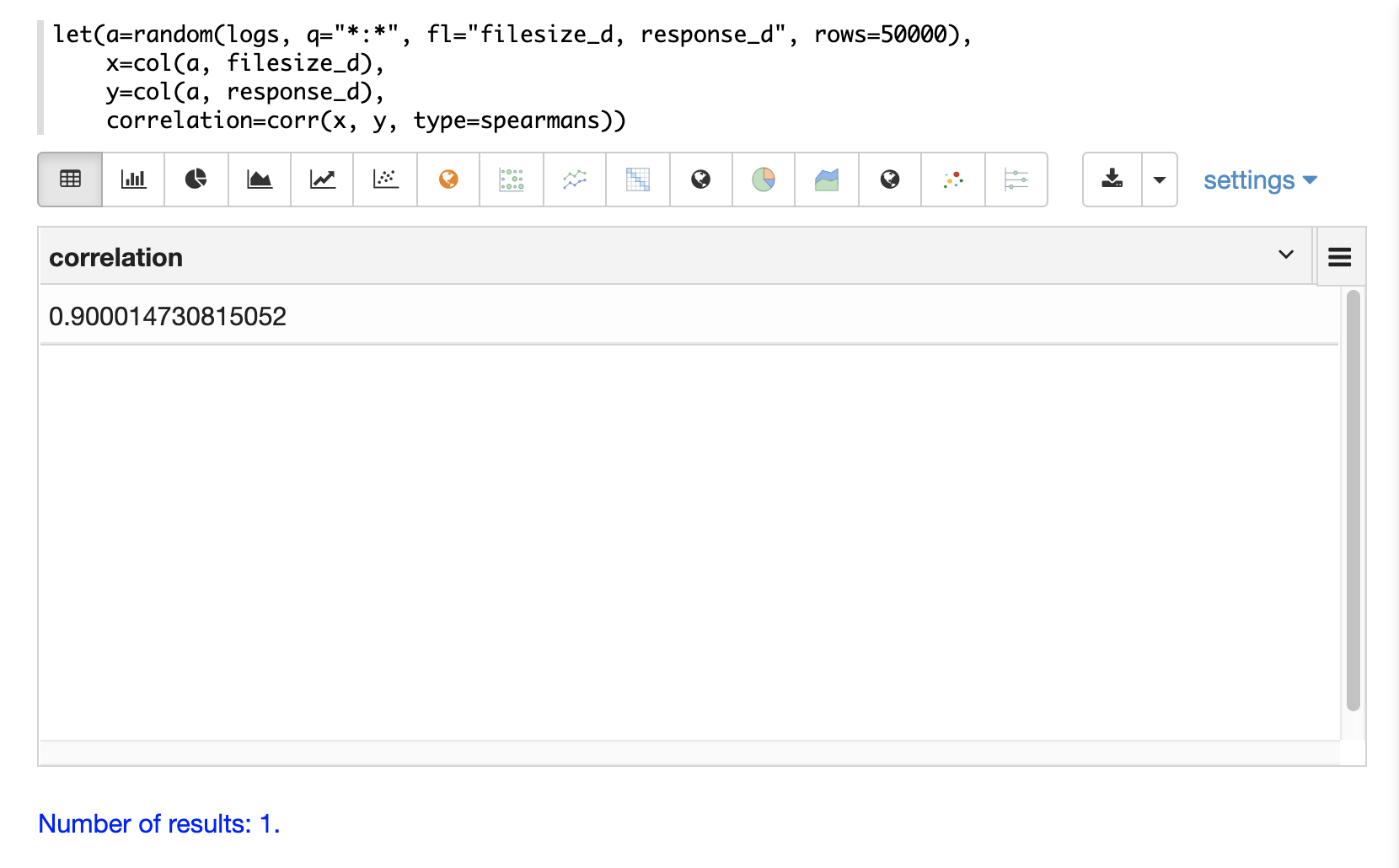
相関行列
相関行列は、2つ以上のベクトルの間の相関を視覚化するための強力なツールです。
corr関数は、行列がパラメータとして渡されると、相関行列を構築します。相関行列は、行列の列を相関させることによって計算されます。
以下の例は、2次元ファセットと組み合わせた相関行列の威力を示しています。
この例では、facet2D関数を使用して、nyc311苦情データベースからフィールドcomplaint_type_sとzip_sにわたる2次元ファセット集計を生成します。上位20の苦情タイプと、各苦情タイプに対する上位25の郵便番号が集計されます。結果は、complaint_type_s、zip_s、およびペアのカウントの各フィールドを含むタプルのストリームです。
次に、pivot関数を使用して、フィールドを行としてzip_sフィールド、列としてcomplaint_type_sフィールドを使用して行列にピボットします。count(*)フィールドは、行列のセルの値を入力します。
次に、corr関数を使用して、行列の列を相関させます。これにより、苦情タイプが出現する郵便番号に基づいて、苦情タイプがどのように相関しているかを示す相関行列が生成されます。別の見方をすると、これは、さまざまな苦情タイプが郵便番号全体でどのように同時に発生する傾向があるかを示しています。
最後に、zplot関数を使用して、相関行列をヒートマップとしてプロットします。
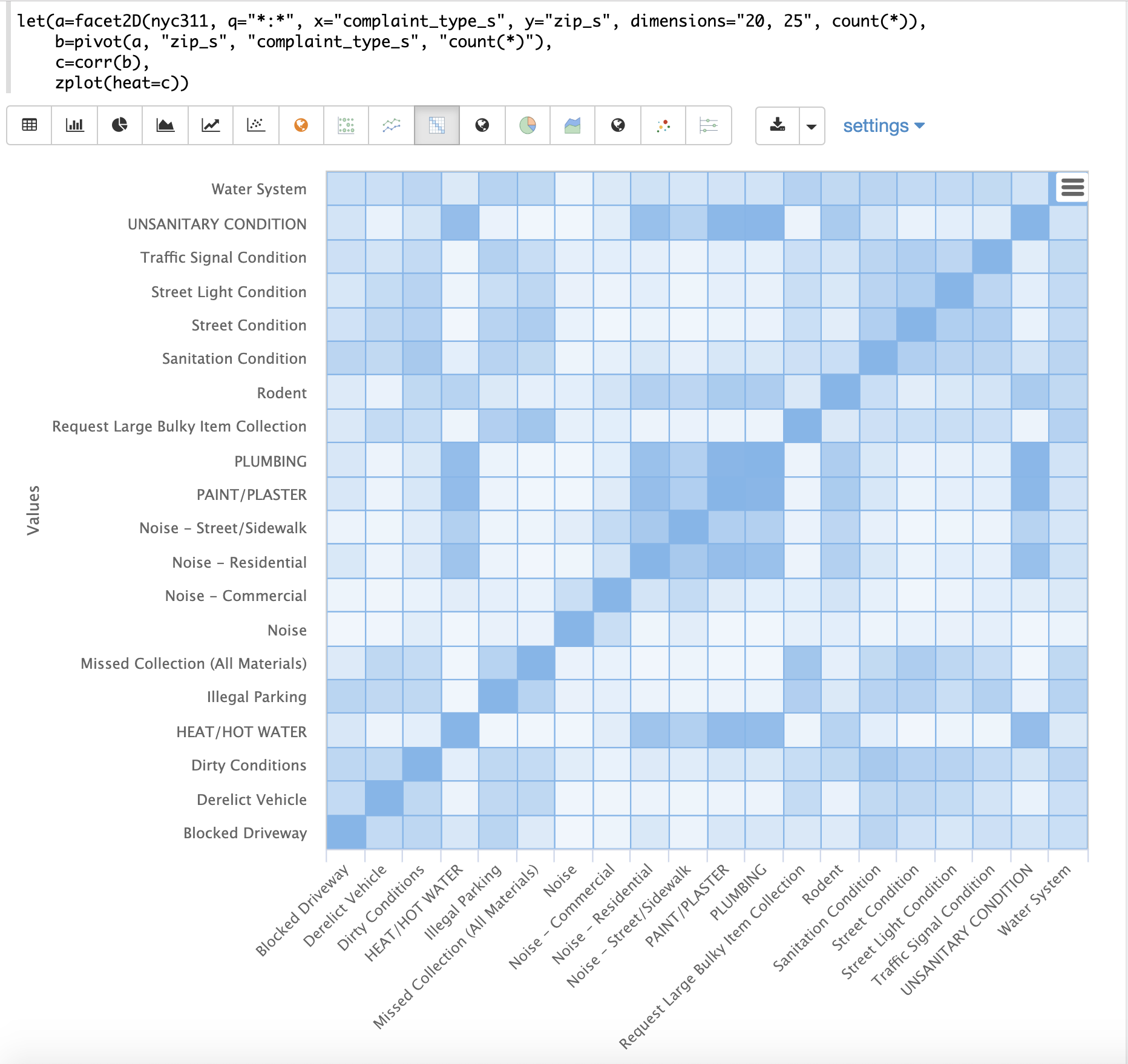
この例では、相関行列が正方形であり、苦情タイプがx軸とy軸の両方に表示されていることに注意してください。ヒートマップのセルの色は、苦情タイプ間の相関の強度を示します。
ヒートマップはインタラクティブなので、セルの1つにマウスを合わせると、セルの値がポップアップ表示されます。
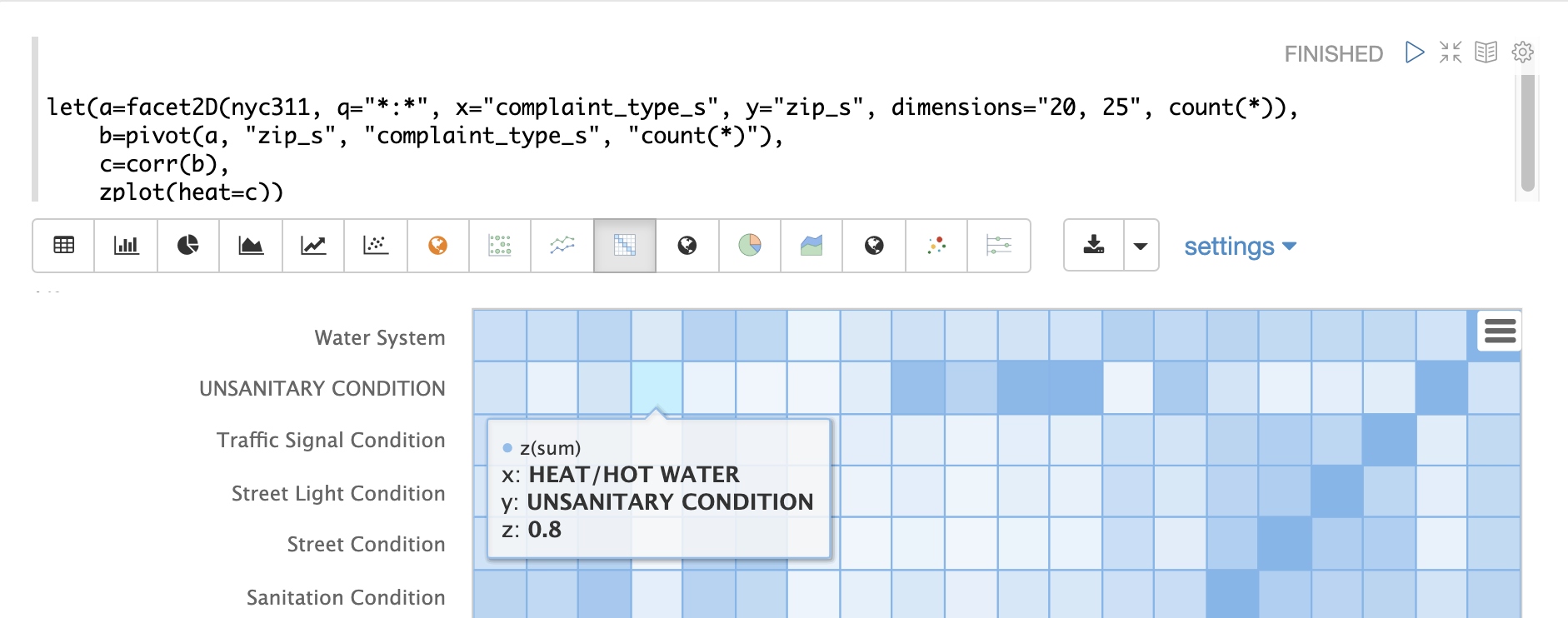
「暖房/温水」と「非衛生的状態」の苦情には、0.8の相関関係がある(小数点以下第1位に四捨五入)ことに注意してください。
共分散と共分散行列
共分散は、相関のスケールされていない尺度です。
cov関数は、2つのデータベクトルの共分散を計算します。
以下の例では、random関数を使用してログコレクションから2つのフィールド(filesize_dとresponse_d)を含むランダムサンプルが抽出されます。フィールドは変数xとyにベクトル化され、次にcov関数を使用して2つのベクトルの共分散が計算されます。
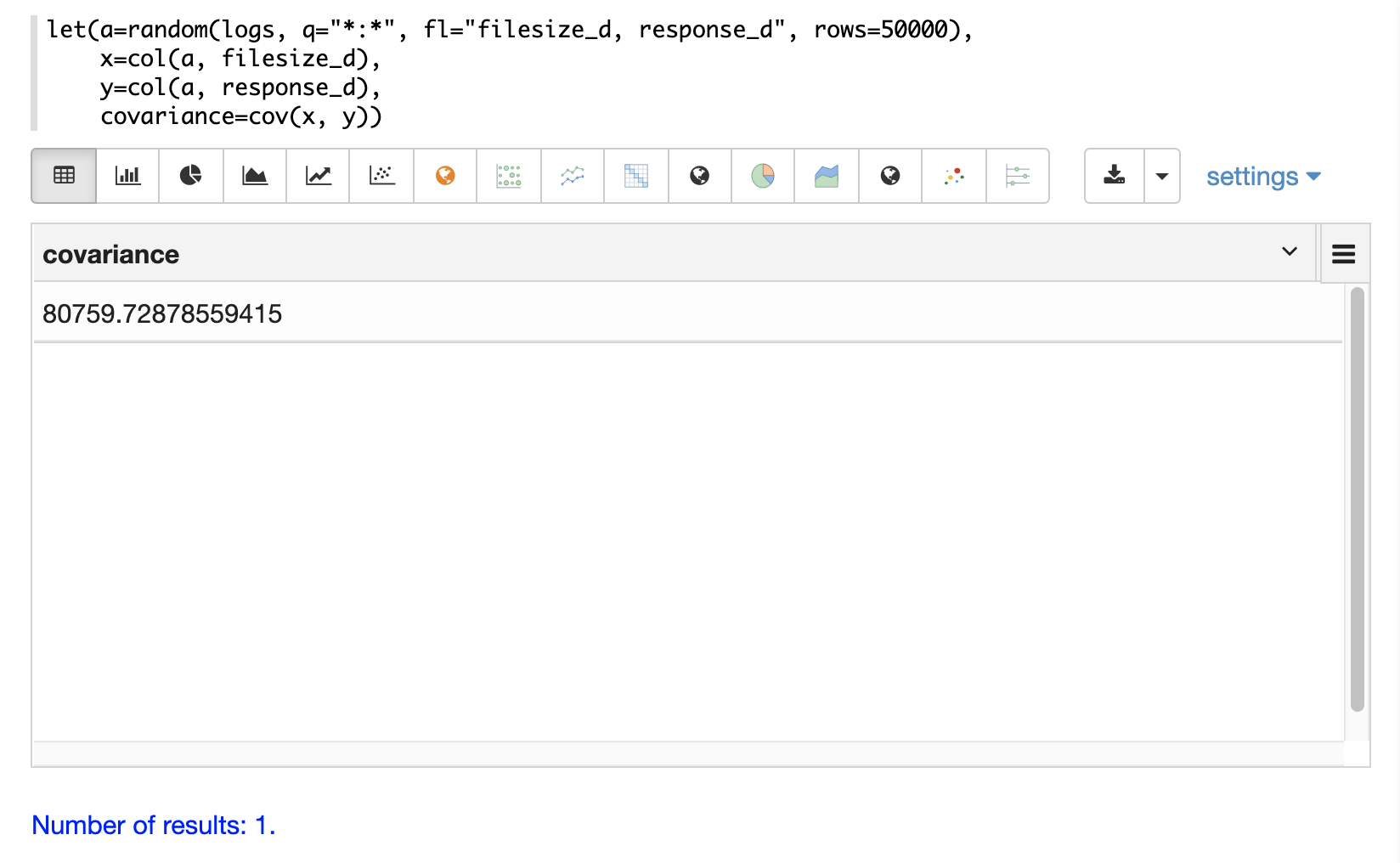
行列がcov関数に渡されると、その行列の列の共分散行列が自動的に計算されます。
以下の例では、xベクトルとyベクトルが行列に追加されることに注意してください。次に行列が転置されて行が列に変わり、行列の列の共分散行列が計算されます。
let(a=random(logs, q="*:*", fl="filesize_d, response_d", rows=50000),
x=col(a, filesize_d),
y=col(a, response_d),
m=transpose(matrix(x, y)),
covariance=cov(m))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"covariance": [
[
4018404.072532102,
80243.3948172242
],
[
80243.3948172242,
1948.3216661122592
]
]
},
{
"EOF": true,
"RESPONSE_TIME": 534
}
]
}
}共分散行列には、次の形式で、2つのベクトルの分散とベクトル間の共分散の両方が含まれています。
x y
x [4018404.072532102, 80243.3948172242],
y [80243.3948172242, 1948.3216661122592]共分散行列は常に正方形です。したがって、3つのベクトルから作成された共分散行列は、3 x 3の行列を生成します。
統計的推論テスト
統計的推論テストは、ランダムサンプルに関する仮説をテストし、p値を返します。p値は、母集団全体のテストの信頼性を推論するために使用できます。
次の統計的推論テストが利用可能です。
-
anova:一元配置分散分析は、2つ以上のランダムサンプルの平均値に統計的に有意な差があるかどうかをテストします。 -
ttest:t検定は、2つのランダムサンプルの平均値に統計的に有意な差があるかどうかをテストします。 -
pairedTtest:ペアt検定は、ペアデータを持つ2つのランダムサンプルの平均値に統計的に有意な差があるかどうかをテストします。 -
gTestDataSet:G検定は、ビン分割された離散データの2つのサンプルが同じ母集団から抽出されたかどうかをテストします。 -
chiSquareDataset:カイ二乗検定は、ビン分割された離散データの2つのサンプルが同じ母集団から抽出されたかどうかをテストします。 -
mannWhitney:マンホイットニー検定は、連続データの2つのサンプルが同じ母集団から抽出されたかどうかをテストするノンパラメトリック検定です。マンホイットニー検定は、t検定の基本的な仮定が満たされていない場合によくt検定の代わりに使用されます。 -
ks:コルモゴロフ-スミルノフ検定は、連続データの2つのサンプルが同じ分布から抽出されたかどうかをテストします。
以下は、2つのランダムサンプルに対して実行されたt検定の簡単な例です。返されたp値が.93であることは、2つのサンプルに平均値の統計的に有意な差がないという帰無仮説を受け入れることができることを意味します。
let(a=random(collection1, q="*:*", rows="1500", fl="price_f"),
b=random(collection1, q="*:*", rows="1500", fl="price_f"),
c=col(a, price_f),
d=col(b, price_f),
e=ttest(c, d))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"e": {
"p-value": 0.9350135639249795,
"t-statistic": 0.081545541074817
}
},
{
"EOF": true,
"RESPONSE_TIME": 48
}
]
}
}変換
統計分析では、統計計算を実行する前にデータセットを変換すると便利なことがよくあります。統計関数ライブラリには、次の一般的な変換が含まれています。
-
rank:元の配列の各要素のランク変換された値を持つ数値配列を返します。 -
log:元の配列の各要素の自然対数を持つ数値配列を返します。 -
log10:元の配列の各要素の底が10の対数を持つ数値配列を返します。 -
sqrt:元の配列の各要素の平方根を持つ数値配列を返します。 -
cbrt:元の配列の各要素の立方根を持つ数値配列を返します。 -
recip:元の配列の各要素の逆数を持つ数値配列を返します。
以下は、対数変換されたデータセットに対して実行されたt検定の例です。
let(a=random(collection1, q="*:*", rows="1500", fl="price_f"),
b=random(collection1, q="*:*", rows="1500", fl="price_f"),
c=log(col(a, price_f)),
d=log(col(b, price_f)),
e=ttest(c, d))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"e": {
"p-value": 0.9655110070265056,
"t-statistic": -0.04324265449471238
}
},
{
"EOF": true,
"RESPONSE_TIME": 58
}
]
}
}逆変換
log、log10、sqrt、およびcbrt関数で変換されたベクトルは、pow関数を使用して逆変換できます。
以下の例は、sqrt関数で変換されたデータを逆変換する方法を示しています。
let(echo="b,c",
a=array(100, 200, 300),
b=sqrt(a),
c=pow(b, 2))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"b": [
10,
14.142135623730951,
17.320508075688775
],
"c": [
100,
200.00000000000003,
300.00000000000006
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}以下の例は、log10関数で変換されたデータを逆変換する方法を示しています。
let(echo="b,c",
a=array(100, 200, 300),
b=log10(a),
c=pow(10, b))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"b": [
2,
2.3010299956639813,
2.4771212547196626
],
"c": [
100,
200.00000000000003,
300.0000000000001
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}recip 関数で変換されたベクトルは、その逆数の逆数を取ることで元のベクトルに戻すことができます。
以下の例は、recip 関数の逆変換の例を示しています。
let(echo="b,c",
a=array(100, 200, 300),
b=recip(a),
c=recip(b))この式が /stream ハンドラーに送信されると、次のように応答します
{
"result-set": {
"docs": [
{
"b": [
0.01,
0.005,
0.0033333333333333335
],
"c": [
100,
200,
300
]
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}