モンテカルロシミュレーション
モンテカルロシミュレーションは、確率的(ランダム)システムの動作をモデル化するためによく使用されます。ユーザーガイドのこのセクションでは、数式を使用してモンテカルロシミュレーションを実行するための基本について説明します。
ランダム時系列
株価の毎日の動きは、しばしば「ランダムウォーク」と表現されます。しかし、それは実際にはどういう意味で、ランダム時系列とはどう違うのでしょうか?以下の例では、モンテカルロシミュレーションを使用して、「ランダムウォーク」とランダム時系列の両方を探ります。
違いを理解するための最初のステップは、終値から始値を引いた値として計算された日次株価収益率を時系列として視覚化することです。
以下の例では、`search`関数を使用して、ティッカー**CVX**(Chevron)の日次株価収益率を1000日間返します。`change_d`フィールド(1日の価格の変化)は、時系列としてプロットされます。
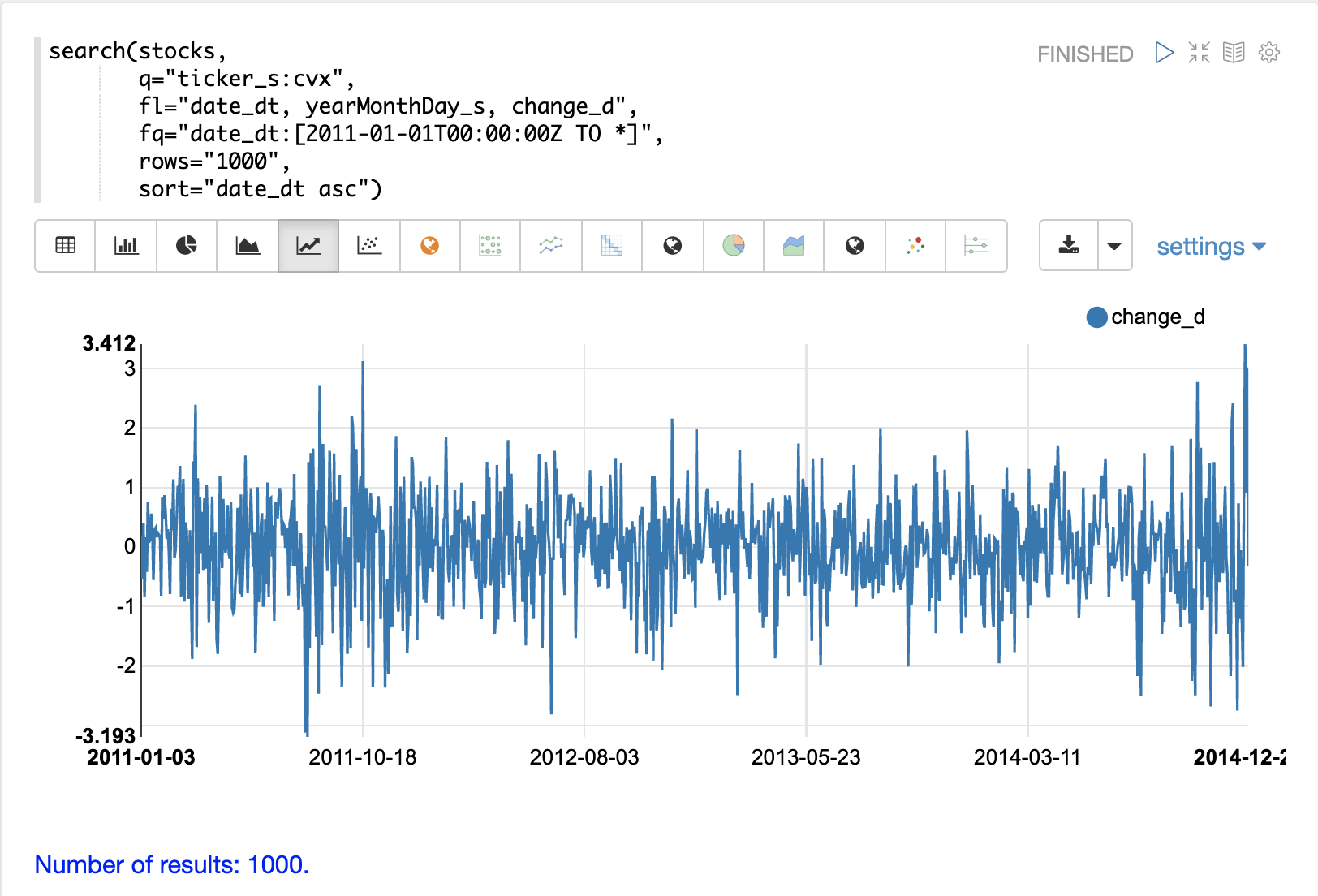
日次価格変化の時系列は、ゼロを上下にランダムに移動することに注意してください。株価が上昇する日もあれば、下落する日もありますが、顕著なパターンやステップ間の依存関係は見られません。これは、これが**ランダム時系列**であるというヒントです。
自己相関
自己相関は、信号がそれ自体と相関する程度を測定します。自己相関を使用して、ベクトルに信号が含まれているか、時系列の値間に依存関係があるかを判断できます。信号がなく、時系列の値間に依存関係がない場合、時系列はランダムです。
`change_d`ベクトルの自己相関をプロットして、実際にランダムであることを確認すると便利です。
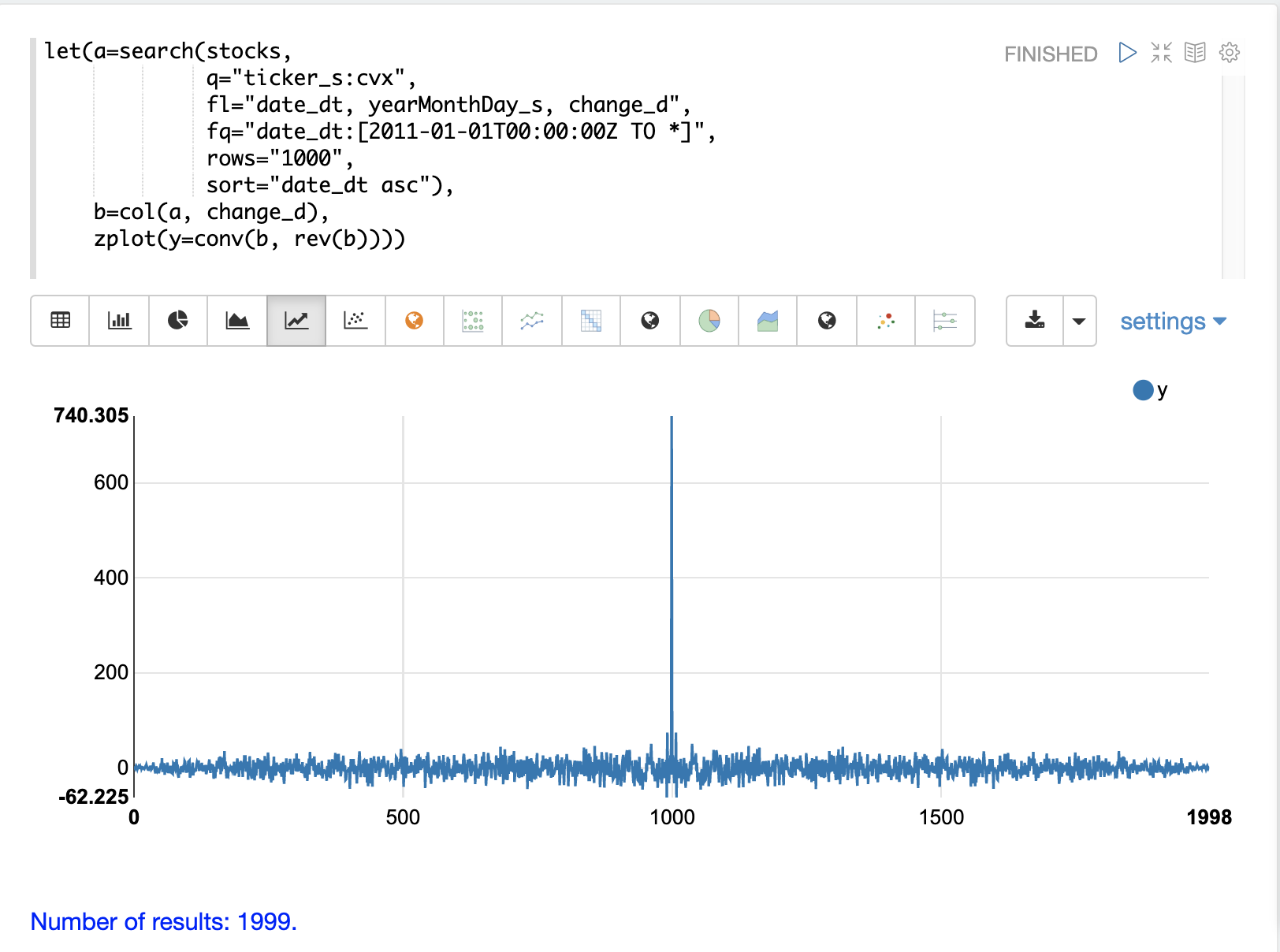
以下の例では、検索結果が変数に設定され、`change_d`フィールドがベクトル化されて変数`b`に格納されます。次に、`conv`(畳み込み)関数を使用して、`change_d`ベクトルを自己相関させます。`conv`関数は、単に`change_d`ベクトルをそれ自体の反転コピーと「畳み込む」ことに注意してください。これは、畳み込みを使用して自己相関を実行するための手法です。ユーザーガイドのデジタル信号処理セクションでは、畳み込みと自己相関の両方について詳しく説明しています。このセクションでは、プロットについてのみ説明します。
このプロットは、conv 関数によって change_d ベクトルが自身とスライド比較された際に計算される相関の強度を示しています。プロットには、ランダムに見える低強度相関の長い期間があることに注目してください。そして中央には、ベクトルが直接揃っている高強度相関のピークがあります。その後には、再び低強度相関の長い期間が続きます。
これは純粋なノイズの自己相関プロットです。毎日の株価の変動はランダムな時系列のようです。
分布の可視化
株価のランダムな日次変動は予測できませんが、確率分布でモデル化できます。時系列をモデル化するために、まず change_d ベクトルの分布を可視化することから始めます。以下の例では、change_d ベクトルを empiricalDistribution 関数を使用してプロットし、データの11ビンヒストグラムを作成しています。分布は正規分布しているように見えることに注意してください。日々の株価変動は正規分布する傾向がありますが、この特性のため、この例では特に CVX が選択されました。
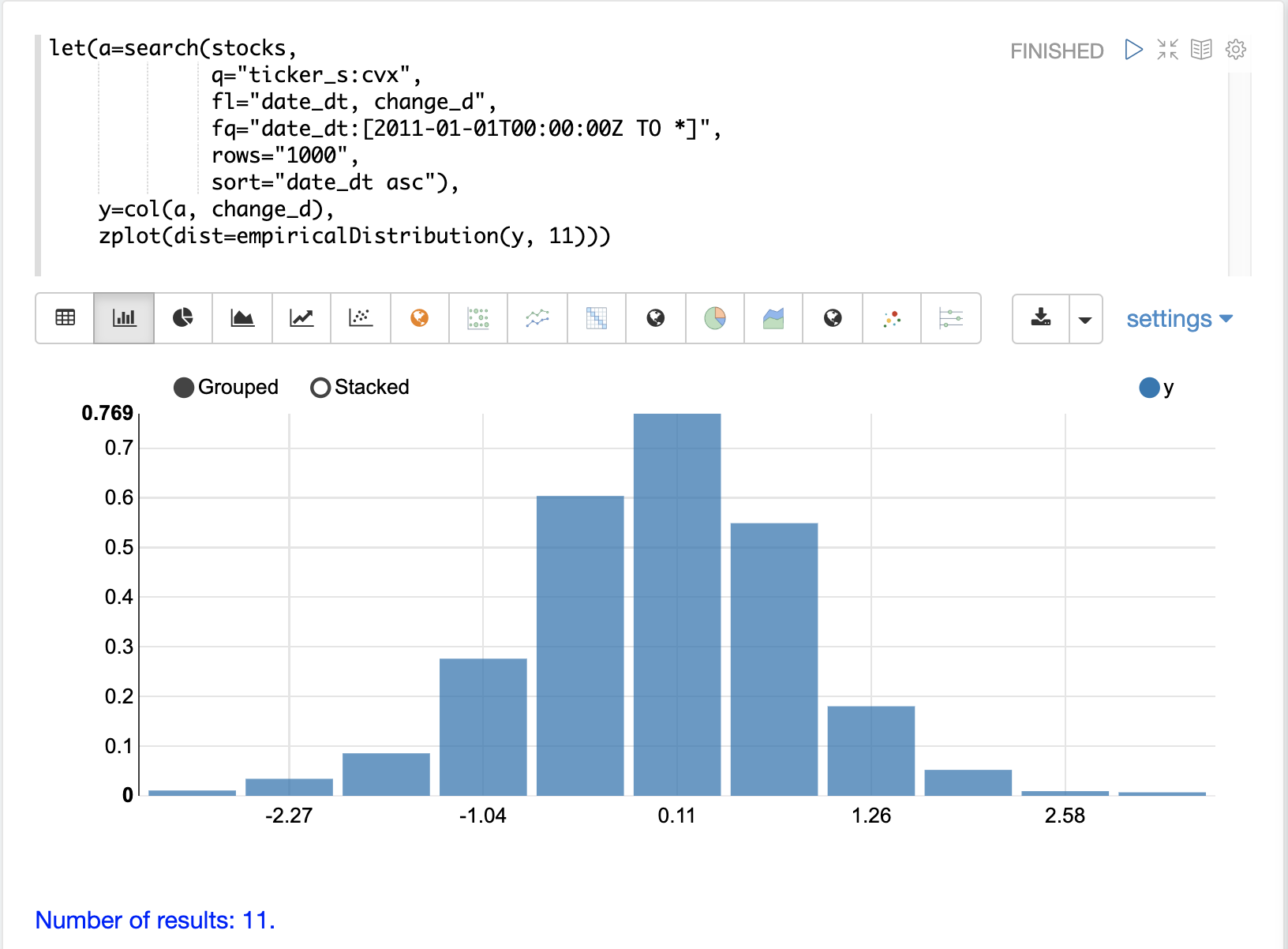
分布への適合
ks 検定は、データベクトルの分布が参照分布に適合するかどうかを判断するために使用できます。以下の例では、change_d ベクトルの**平均**(mean)と**標準偏差**(stddev)を持つ**正規分布**を参照分布として、ks 検定を実行しています。 ks 検定は、参照分布を change_d ベクトル自体と比較して、正規分布に適合するかどうかを確認しています。
以下の例では、ks 検定のp値が.16278であることに注意してください。通常、p値が.05以下の場合、ベクトルが参照分布から抽出された可能性があるという検定の帰無仮説を無効にするために使用されます。
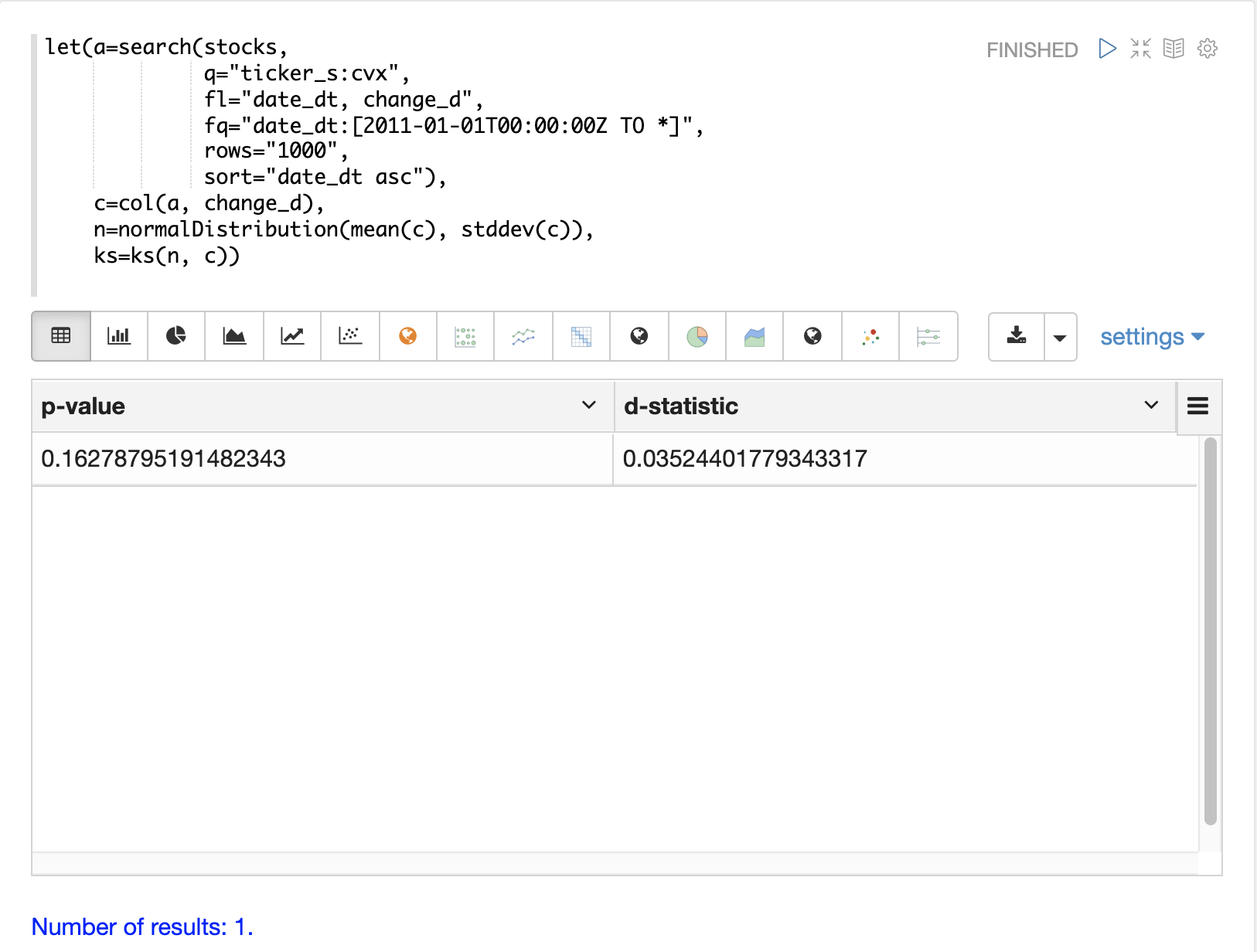
かなり敏感である傾向がある ks 検定は、正規分布に見える視覚化を確認しました。このため、change_d ベクトルの**平均**と**標準偏差**を持つ正規分布は、以下のモンテカルロシミュレーションでシェブロンの日次株価収益を表すために使用されます。
モンテカルロ
日次株価収益データに分布を適合させたので、monteCarlo 関数を使用して、その分布を用いたシミュレーションを実行できます。
monteCarlo 関数は、指定された回数だけ実行されます。各実行で、一連の変数を設定し、単一の 数値を返す最後の関数を1つ実行します。 monteCarlo 関数は、各実行の結果をベクトルに収集して返します。最後の関数には、通常、各実行で確率分布から抽出される1つ以上の変数があります。サンプルを抽出するには、sample 関数を使用します。
シミュレーションの結果配列は、シミュレーション結果の確率を理解するために、経験分布として扱うことができます。
以下の例では、monteCarlo 関数を使用して、100日間の株価収益の合計収益の分布をシミュレートしています。
この例では、change_d ベクトルの**平均**と**標準偏差**から normalDistribution が作成されます。 monteCarlo 関数は、正規分布から100個のサンプルを抽出して100日間の株価収益を表し、サンプルのベクトルを変数 d に設定します。
次に、add 関数は100日間のサンプルからの合計収益を計算します。 add 関数の出力は、monteCarlo 関数によって収集されます。これは50000回繰り返され、各実行では正規分布から異なるサンプルセットが抽出されます。
シミュレーションの結果は変数 s に設定され、これには50000回の実行からの合計収益が含まれています。
次に、empiricalDistribution 関数を使用して、シミュレーションの出力を50ビンヒストグラムとして可視化します。この分布は、ティッカー CVX の100日間の株価収益からのさまざまな合計収益の確率を視覚化します。
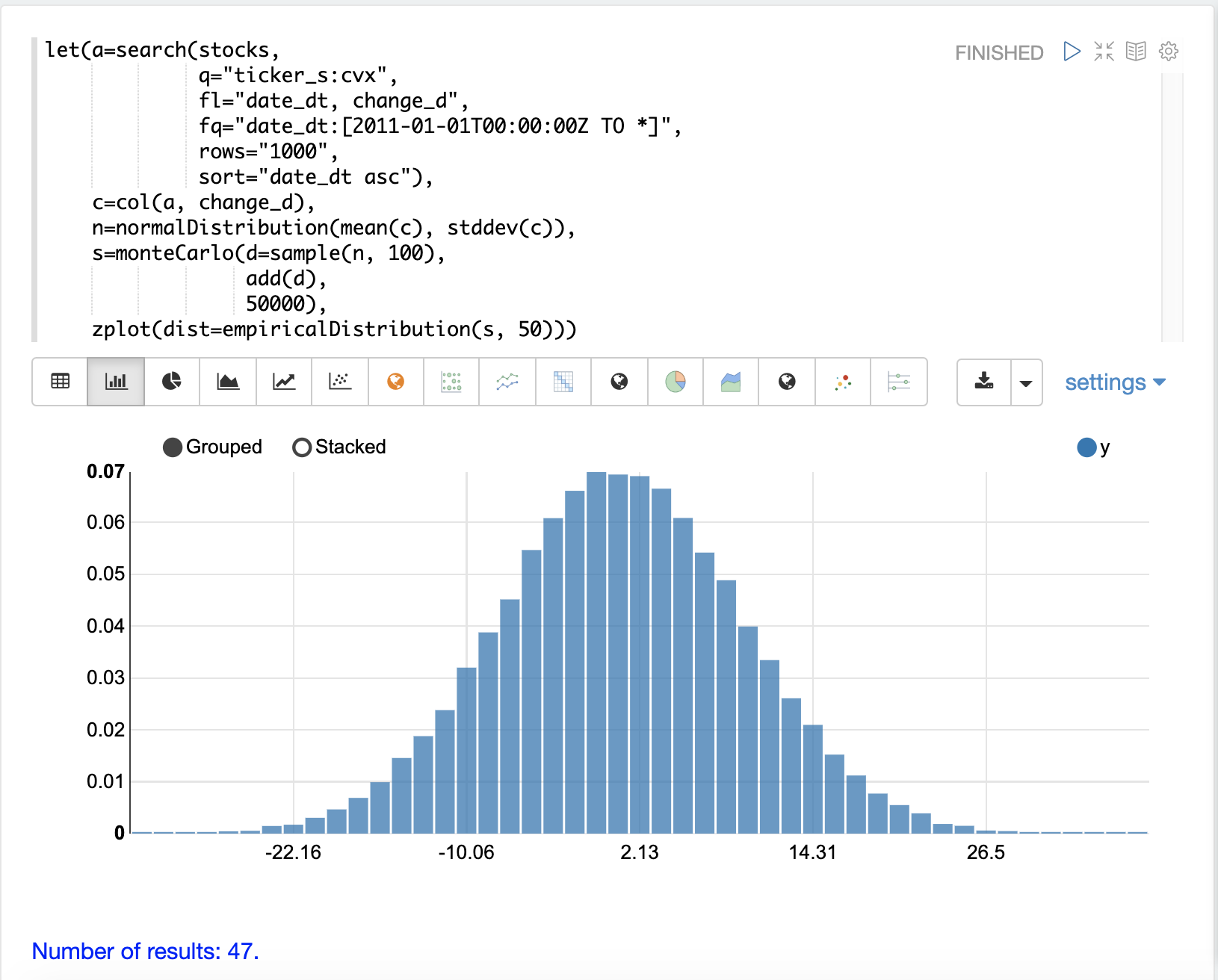
probability 関数と cumulativeProbability 関数を使用して、empiricalDistribution について詳しく学ぶことができます。たとえば、probability 関数を使用して、100日間の株価収益から非負の収益を得る確率を計算できます。
以下の例では、probability 関数を使用して、シミュレーションの empiricalDistribution から0〜40の範囲の収益の確率を返しています。
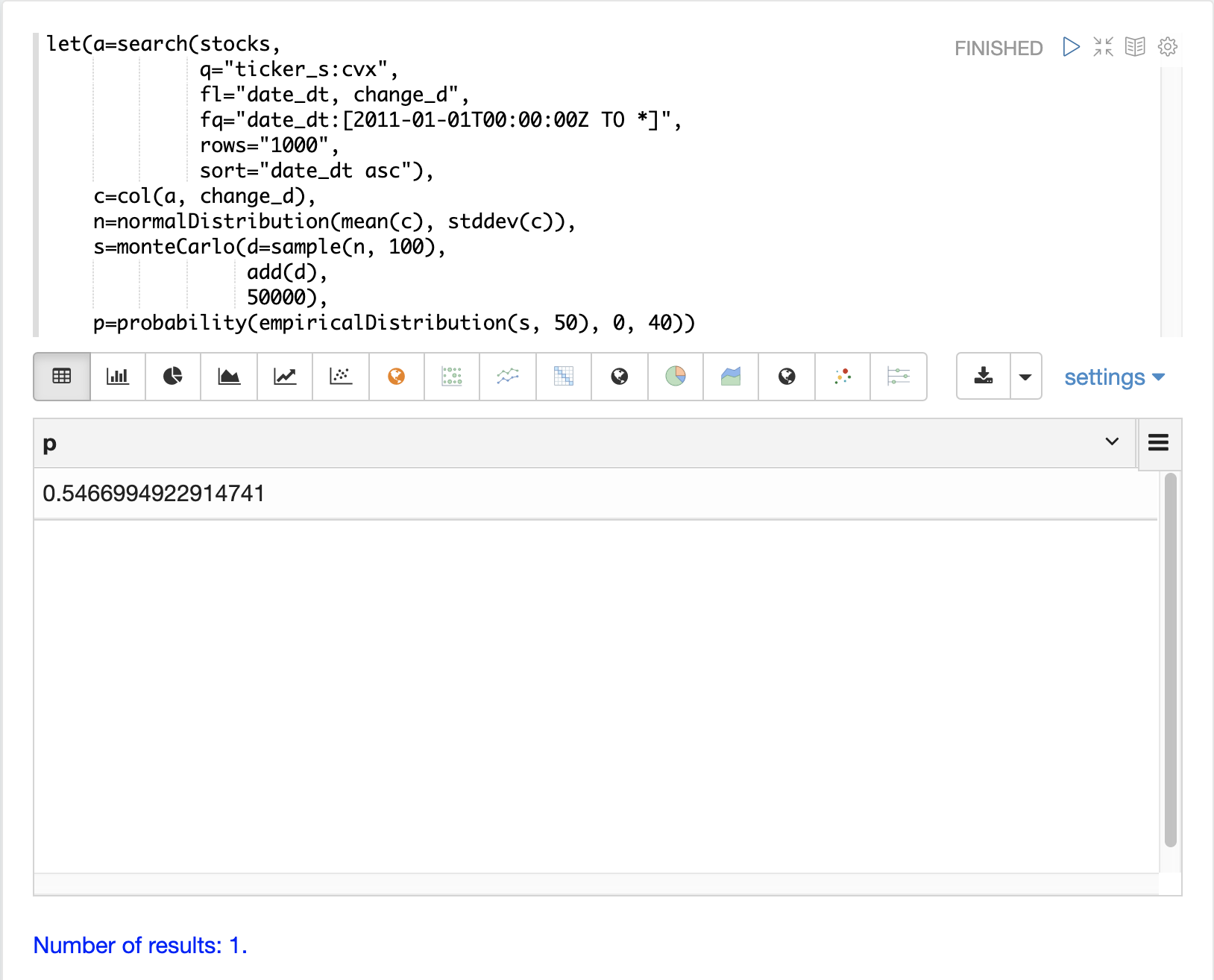
ランダムウォーク
monteCarlo 関数は、日次株価収益の normalDistribution から日次株価のランダムウォークをモデル化するためにも使用できます。ランダムウォークとは、各ステップが前のステップにランダムサンプルを追加することによって計算される時系列です。これにより、各値が前の値に依存する時系列が作成され、株価の自己相関がシミュレートされます。
以下の例では、モンテカルロの各反復で変数 v にランダムサンプルを追加することにより、ランダムウォークを実現しています。変数 v は反復間で維持されるため、各反復では v の前の値が使用されます。 double 関数は、各反復で実行される最後の関数であり、v の値をdoubleとして返します。この例では、1000回反復して1000ステップのランダムウォークを作成します。
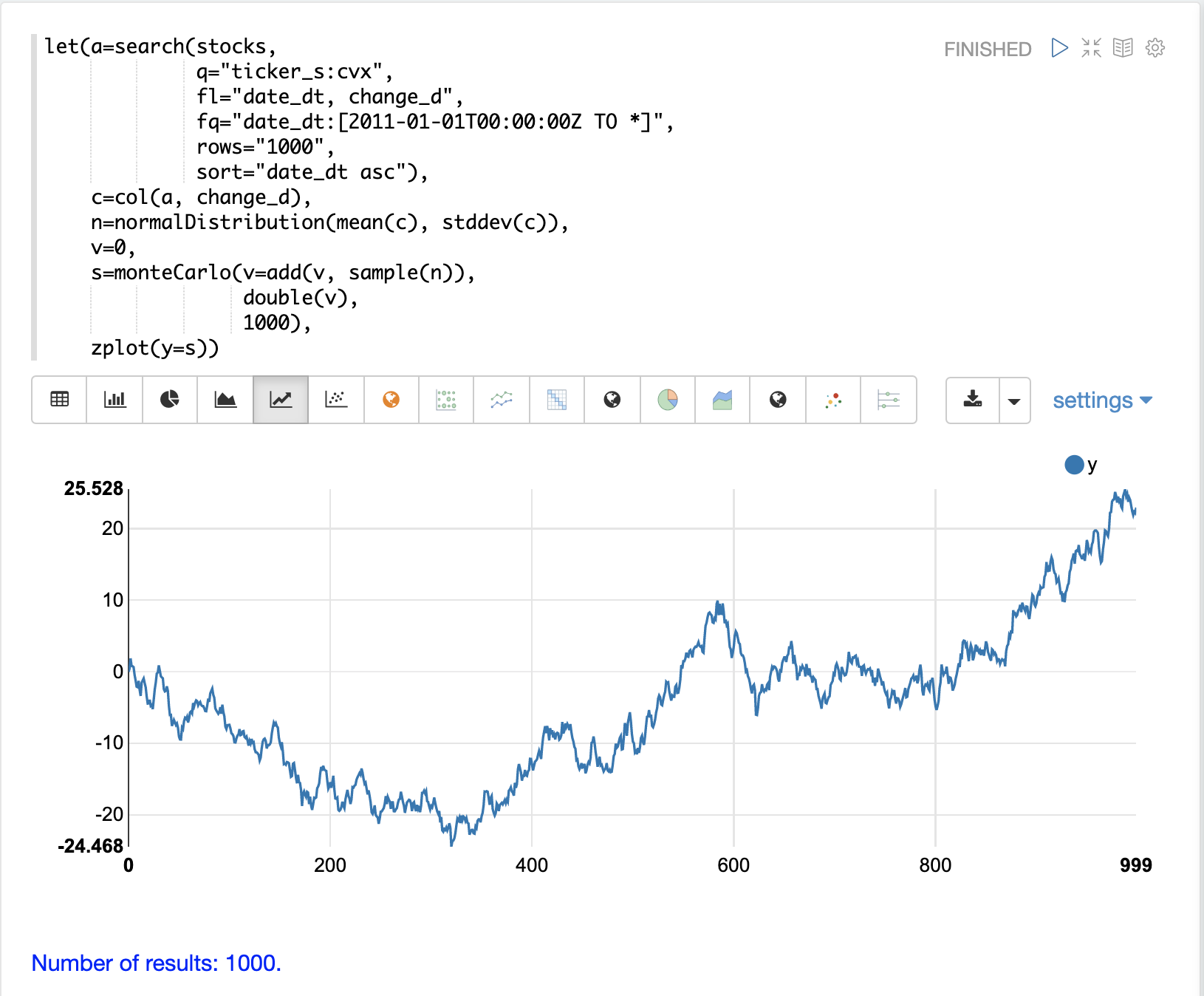
ステップ間の依存関係によって引き起こされる日次株価の自己相関は、日次株価のランダムな変化とは非常に異なるプロットを生成することに注意してください。
多変量正規分布
multiVariateNormalDistribution 関数は、2つ以上の正規分布変数をモデル化およびシミュレートするために使用できます。また、変数間の**相関**をモデルに組み込むことで、相関が結果にどのように影響するかを調べることができます。
以下の例では、2つの株式の合計日次収益のシミュレーションについて説明します。前の例からの CVX ティッカー(シェブロン)とともに、ALL ティッカー(オールステート)が使用されます。
相関と共分散
多変量シミュレーションは、相関が結果に及ぼす影響を示しています。実際のシミュレーションを開始する前に、オールステートとシェブロンの株価収益間の相関と共分散を理解しておくと役立ちます。
以下の例では、2つの検索を実行して、オールステートとシェブロンのすべての日次株価収益を取得しています。両方の収益からの change_d ベクトルは変数(all と cvx)に読み込まれ、2つのベクトルのピアソンの相関が corr 関数で計算されます。
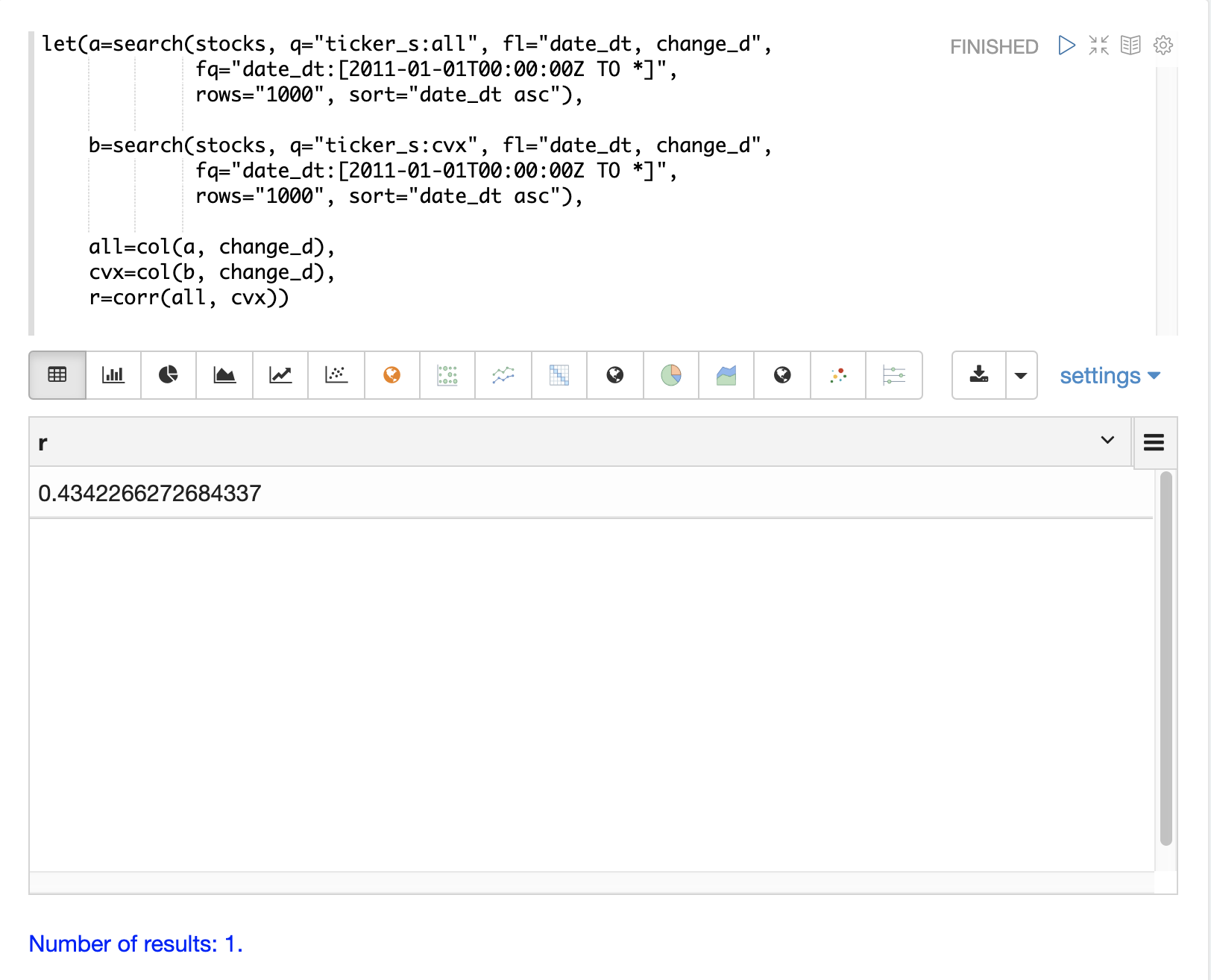
共分散は、相関のスケールされていない尺度です。共分散は多変量シミュレーションで使用される尺度であるため、2つの株価収益の共分散も計算すると役立ちます。以下の例は、共分散を計算しています。
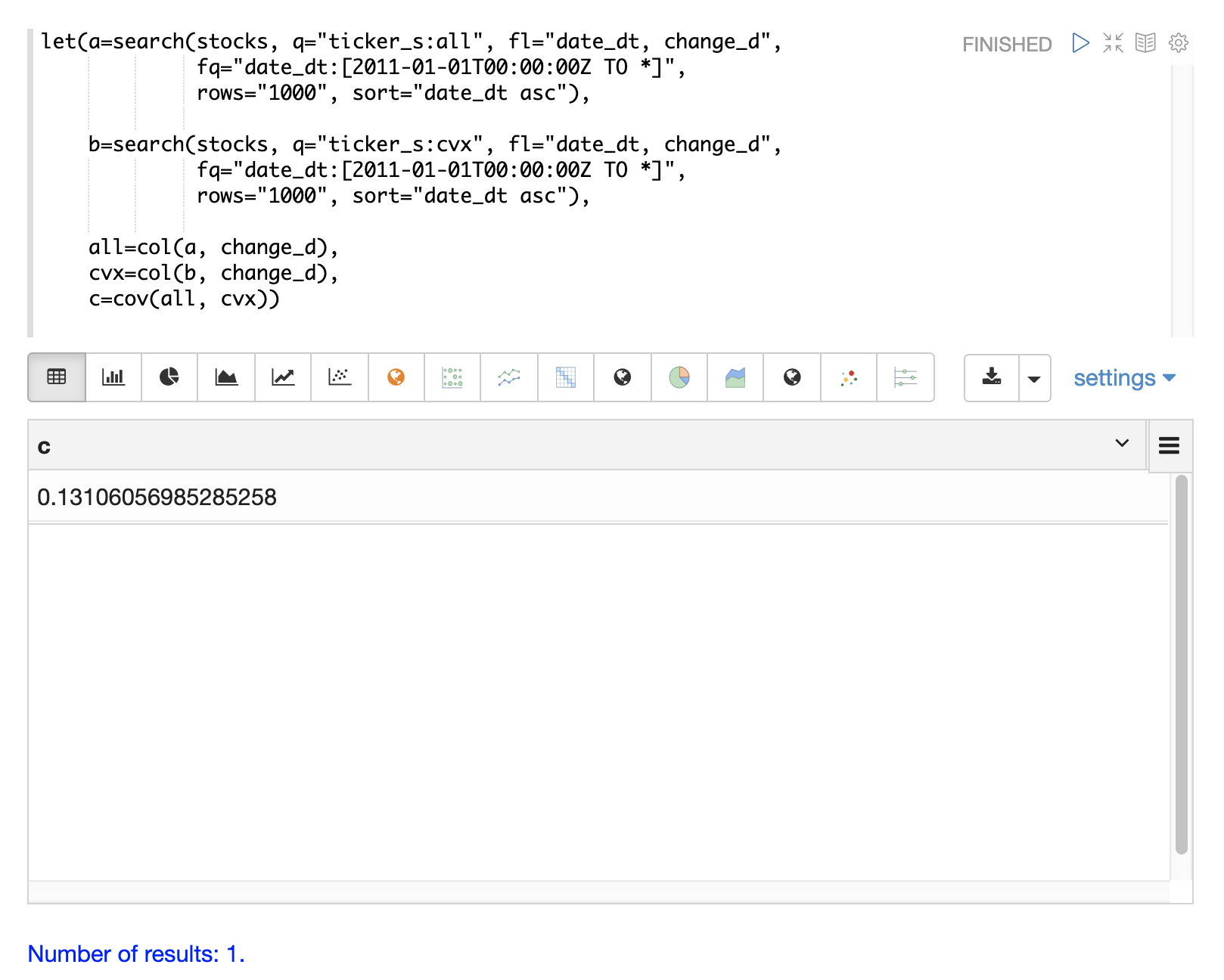
共分散行列
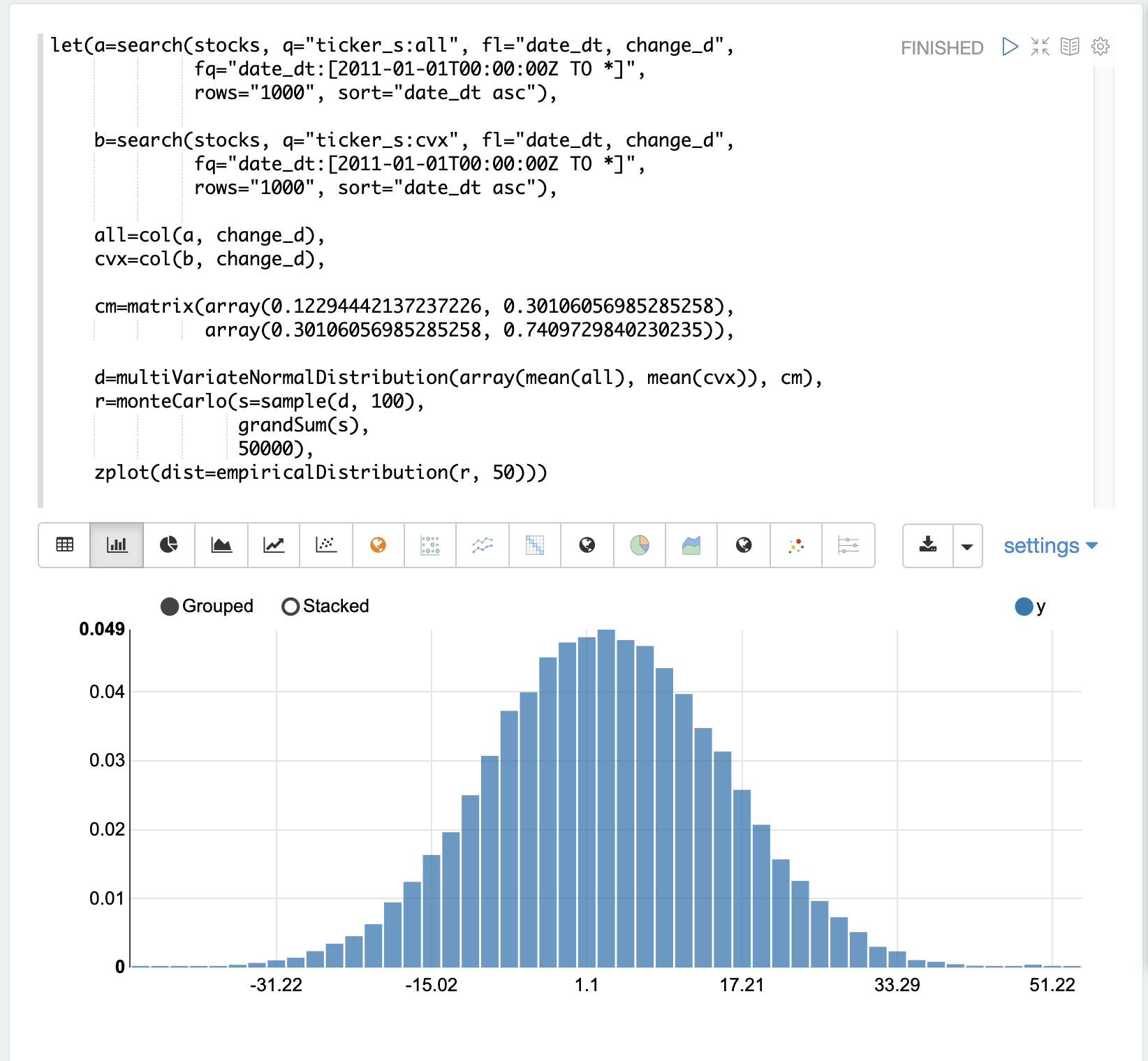
multiVariateNormalDistribution に実際に必要なのは共分散行列です。これは、2つの株価収益ベクトルの分散と2つのベクトル間の共分散の両方を含んでいるためです。 cov 関数は、行列の列の共分散行列を計算します。
以下の例は、all ベクトルと cvx ベクトルを行列に行として追加することにより、共分散行列を計算する方法を示しています。次に、行列は transpose 関数で転置され、all ベクトルが最初の列、cvx ベクトルが2番目の列になります。
次に、cov 関数は行列の列の共分散行列を計算し、結果を返します。
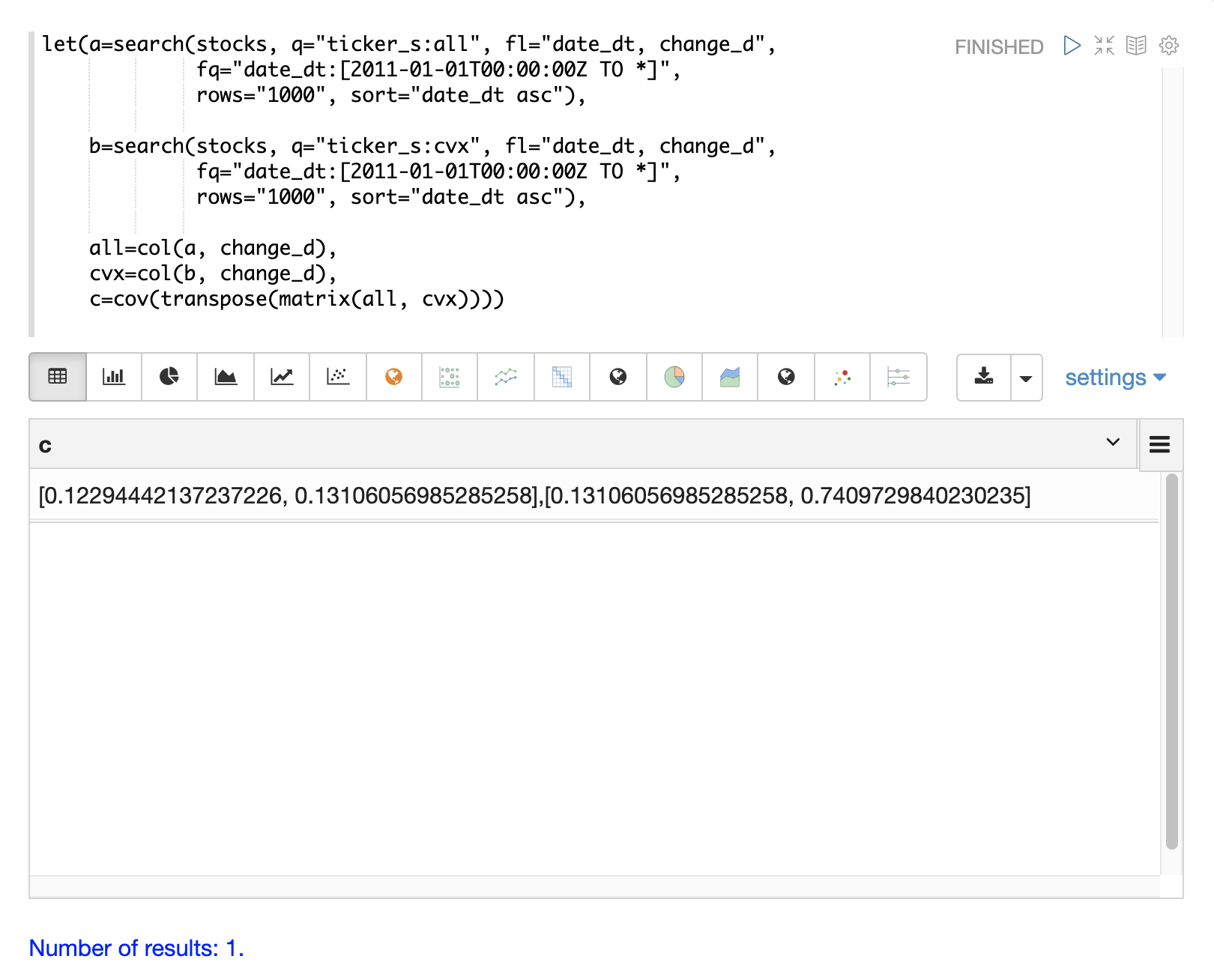
共分散行列は、各ベクトルの分散とベクトル間の共分散を次のように含む正方行列です。
all cvx
all [0.12294442137237226, 0.13106056985285258],
cvx [0.13106056985285258, 0.7409729840230235]多変量シミュレーション
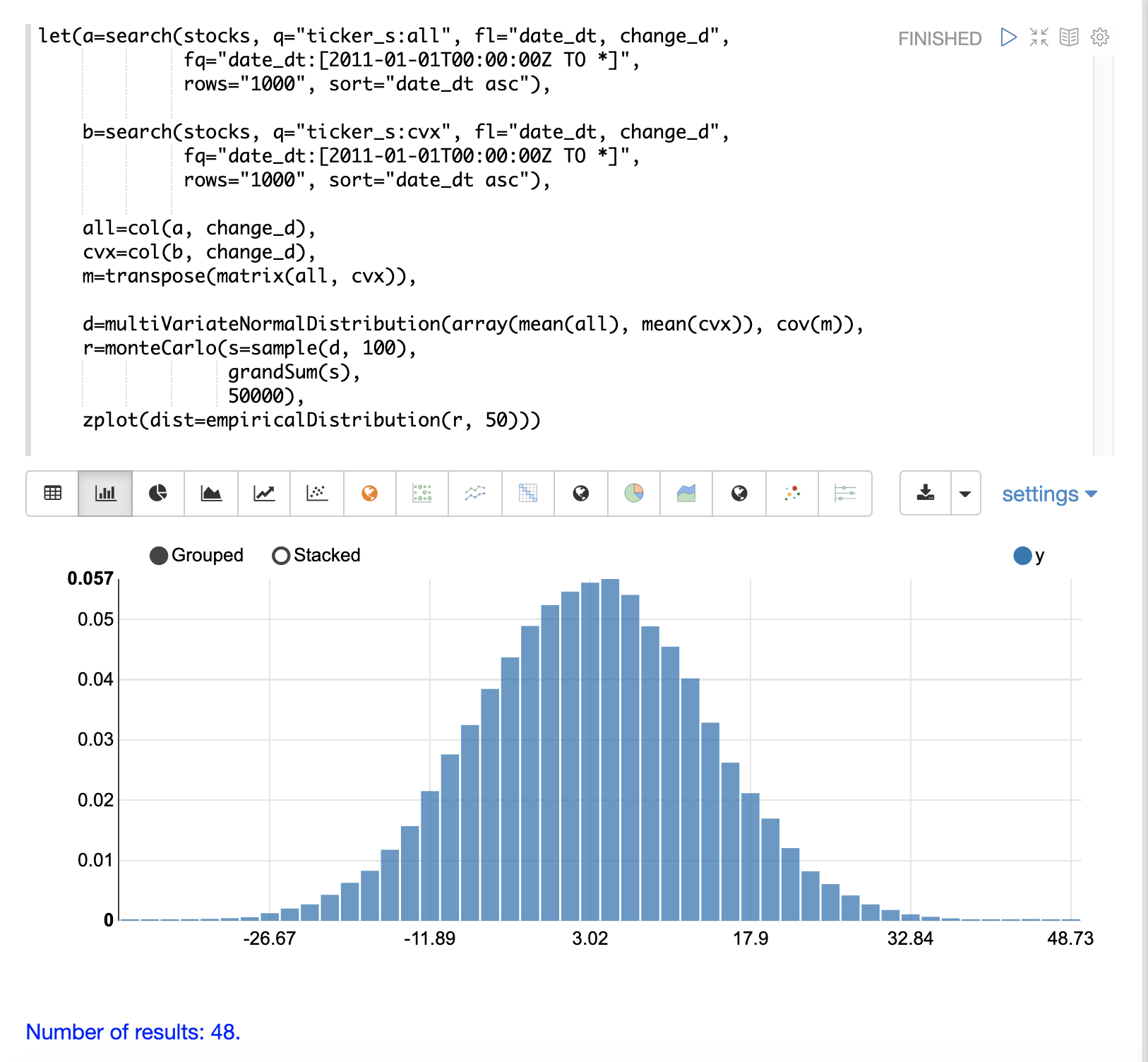
以下の例では、multiVariateNormalDistribution を使用した2つの株式ティッカーによるモンテカルロシミュレーションを示しています。
この例では、2つの株式ティッカー all(オールステート)と cvx(シェブロン)の change_d フィールドを持つ結果セットが取得され、ベクトルに読み込まれます。
次に、2つのベクトルから行列が作成され、転置されるため、行列には2つの列が含まれます。1つは all ベクトル、もう1つは cvx ベクトルです。
次に、multiVariateNormalDistribution は2つのパラメーターで作成されます。最初のパラメーターは mean 値の配列です。この場合は、all ベクトルと cvx ベクトルの平均です。2番目のパラメーターは、2つのベクトルの2列行列から作成された共分散行列です。
monteCarlo 関数は、各反復で multiVariateNormalDistribution から100個のサンプルを抽出してシミュレーションを実行します。各サンプルセットは、all 分布と cvx 分布からの株価収益サンプルを含む100行2列の行列です。列の分布は、multiVariateNormalDistribution の作成に使用された正規分布と一致します。サンプル列の共分散は、共分散行列と一致します。
各反復で、grandSum 関数を使用してサンプル行列のすべての値を合計し、両方の株式の合計株価収益を取得します。
シミュレーションの出力は、単一の株式ティッカーシミュレーションとまったく同じ方法で経験分布として扱うことができるベクトルです。この例では、50ビンヒストグラムとしてプロットされ、ティッカー all と cvx の100日間の株価収益からのさまざまな合計収益の確率を視覚化します。