機械学習

このセクションでは、数学式のユーザーガイドにおける機械学習関数について説明します。

距離と距離行列

distance関数は、2つの数値配列の距離、または行列の列の距離行列を計算します。

実際の距離計算を実行する関数を返す、6つの距離測定関数があります。

euclidean（デフォルト）
manhattan
canberra
earthMovers
cosine
haversineMeters（地理空間距離測定）

距離測定関数は、距離測定をサポートするすべての機械学習関数で使用できます。

以下は、2つの数値配列に対するユークリッド距離の計算例です。

let(a=array(20, 30, 40, 50),
    b=array(21, 29, 41, 49),
    c=distance(a, b))

この式が/streamハンドラに送信されると、次のように応答します。

{
  "result-set": {
    "docs": [
      {
        "c": 2
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

以下では、マンハッタン距離を使用して距離が計算されます。

let(a=array(20, 30, 40, 50),
    b=array(21, 29, 41, 49),
    c=distance(a, b, manhattan()))

この式が/streamハンドラに送信されると、次のように応答します。

{
  "result-set": {
    "docs": [
      {
        "c": 4
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 1
      }
    ]
  }
}

距離行列

距離行列は、2つ以上のベクトル間の距離を視覚化する強力なツールです。

distance関数は、パラメータとして行列が渡された場合、距離行列を構築します。距離行列は、行列の**列**に対して計算されます。

以下の例は、2次元ファセットと組み合わせた距離行列の威力を示しています。

この例では、facet2D関数が使用され、nyc311苦情データベースからcomplaint_type_sフィールドとzip_sフィールドに対して2次元ファセット集計が生成されます。苦情の種類の上位20件と、各苦情の種類の上位25件の郵便番号が集計されます。結果は、それぞれcomplaint_type_s、zip_s、およびペアのカウントを含むタプルのストリームになります。

次に、pivot関数が使用され、フィールドがzip_sフィールドを**行**として、complaint_type_sフィールドを**列**として持つ**行列**にピボットされます。count(*)フィールドは、行列のセルの値を設定します。

次に、distance関数が使用され、cosine距離を使用して行列の列の距離行列が計算されます。これにより、出現する郵便番号に基づいて苦情の種類間の距離を示す距離行列が生成されます。

最後に、zplot関数は、距離行列をヒートマップとしてプロットするために使用されます。ヒートマップは、ベクトル間の距離が小さくなるにつれて色の強度が増加するように構成されていることに注意してください。

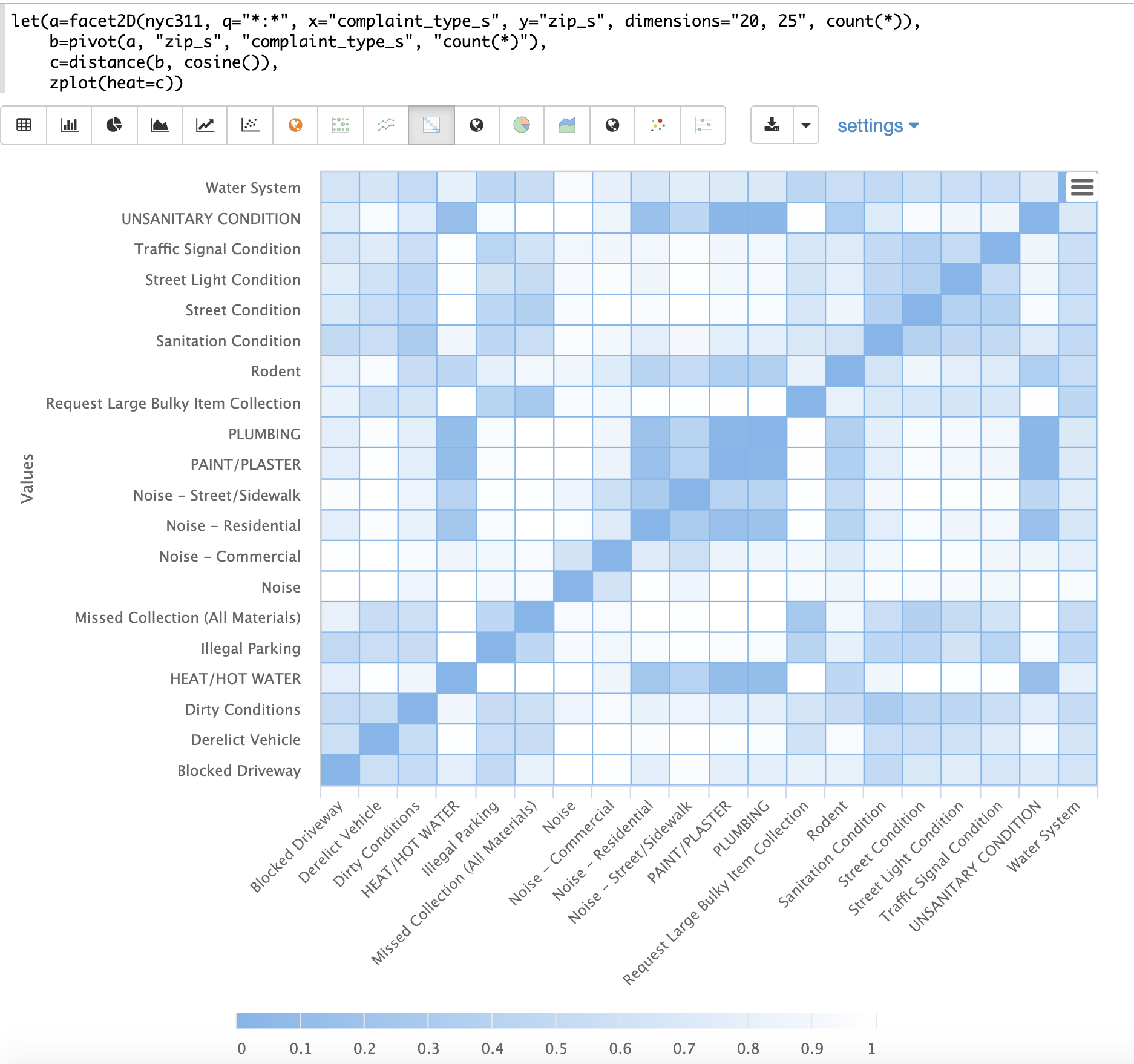
$distance$

ヒートマップはインタラクティブであるため、セルのいずれかにマウスオーバーすると、セルの値がポップアップ表示されます。

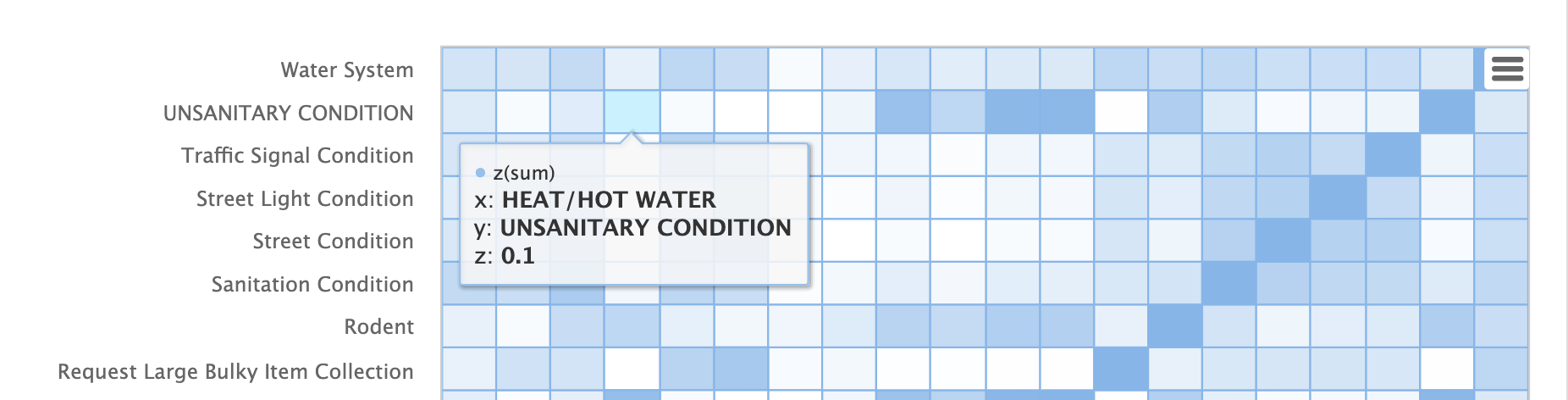
$distanceview$

HEAT/HOT WATERとUNSANITARY CONDITIONの苦情は、コサイン距離が0.1（小数点以下第1位に四捨五入）であることに注意してください。

K-Nearest Neighbor (KNN)

knn関数は、検索ベクトルを使用して行列の行を検索し、k-最近傍の行列を返します。これにより、結果セットに対する二次ベクトル検索が可能になります。

knn関数は、次の距離測定関数のいずれかを指定することで、距離測定の変更をサポートします。

euclidean（デフォルト）
manhattan
canberra
earthMovers
cosine
haversineMeters（地理空間距離測定）

以下の例は、集計結果セットに対して二次検索を実行する方法を示しています。この例では、nyc311苦情データベースにおいて、郵便番号10280と同様の苦情の種類を持つ郵便番号を見つけることを目標としています。

この例における最初のステップは、facet2D関数を用いて、zip_sフィールドとcomplaint_type_sフィールドに対して2次元集計を実行することです。この例では、マンハッタン区のトップ119の郵便番号と、各郵便番号のトップ5の苦情の種類を計算します。結果は、zip_s、complaint_type_s、およびその組み合わせのcount(*)を含むタプルのリストになります。

タプルのリストは、次にpivot関数を使用して行列に**ピボット**されます。この例におけるpivot関数は、郵便番号の行と苦情の種類の列を持つ行列を返します。タプルからのcount(*)フィールドは、行列のセルに入力されます。この行列は、二次検索行列として使用されます。

次のステップは、郵便番号10280のベクトルを見つけることです。これは、例では3つのステップで行われます。最初のステップは、getRowLabels関数を使用して行列から行ラベルを取得することです。この場合の行ラベルは、pivot関数によって入力された郵便番号です。次に、indexOf関数を使用して、行ラベルのリスト内にある"10280"郵便番号の**インデックス**を見つけます。次に、rowAt関数を使用して、行列からその**インデックス**にあるベクトルを返します。このベクトルが**検索ベクトル**です。

これで、行列と検索ベクトルが得られたので、knn関数を使用して検索を実行できます。この例では、knn関数は、Kを5に設定し、**コサイン**距離を使用して、検索ベクトルで行列を検索します。コサイン距離は、この例のようにスパースベクトルを比較する場合に便利です。knn関数は、検索ベクトルに最も近い上位5つの近傍を持つ行列を返します。

knn関数は、戻り値の行列に行と列のラベルを入力し、各行の**距離**のベクトルを行列の属性として追加します。

この例では、zplot関数は、getRowLabels関数とgetAttribute関数を使用して、行ラベルと距離ベクトルを抽出します。topFeatures関数は、各郵便番号ベクトルのトップ5の列ラベルを、各列のカウントに基づいて抽出するために使用されます。次に、zplotは、Zeppelin-Solrで表形式で視覚化できる形式でデータを出力します。

$knn$

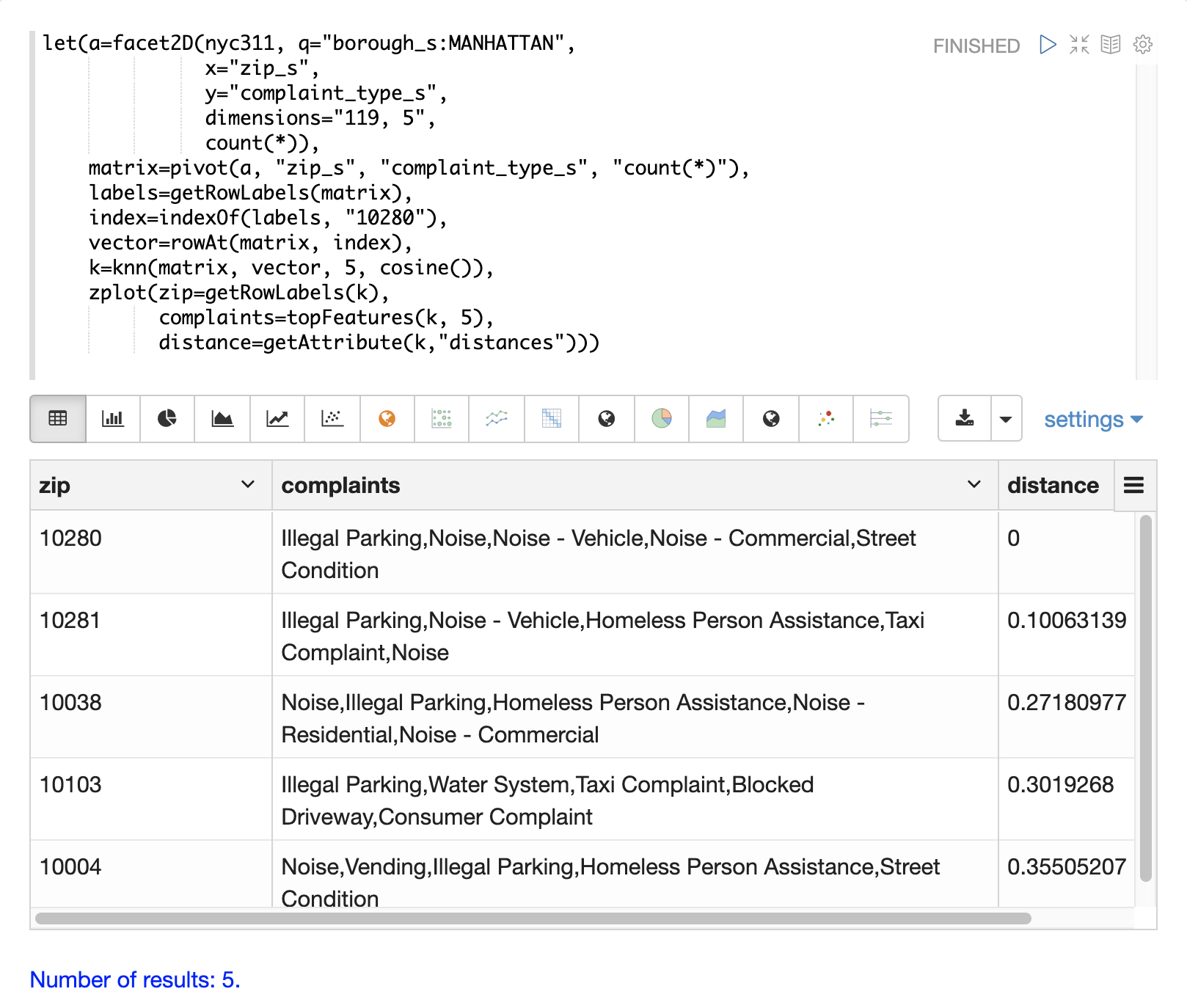
上の表は、knn関数によって返された各郵便番号と、苦情のリストと距離を示しています。これらは、上位5つの苦情の種類に基づいて、郵便番号10280と最も類似した郵便番号です。

K-Nearest Neighbor回帰

K-最近傍回帰は、非線形、二変量、および多変量の回帰手法です。KNN回帰は遅延学習技術であり、事前にトレーニングセットにモデルを適合させません。代わりに、観測値と結果のトレーニングセット全体がメモリに保持され、k-最近傍の結果を平均することで予測が行われます。

knnRegress関数は、最近傍回帰を実行するために使用されます。

2D非線形回帰

以下の例は、2D散布図に適用されたKNN回帰の**回帰プロット**を示しています。

この例では、random関数を用いて、filesize_dフィールドとeresponse_dフィールドの2つのフィールドを含むlogsコレクションから500個のランダムサンプルを抽出します。次に、サンプルはベクトル化され、filesize_dフィールドは変数**x**に割り当てられたベクトルに格納され、eresponse_dベクトルは変数yに格納されます。次に、最近傍パラメータとして20を使用してknnRegress関数が適用され、値を予測するために使用できるKNN関数が返されます。次に、元のxベクトルの値を予測するために、KNN関数に対してpredict関数が呼び出されます。最後に、zplotを使用して、元のxとyベクトルと予測値をプロットします。

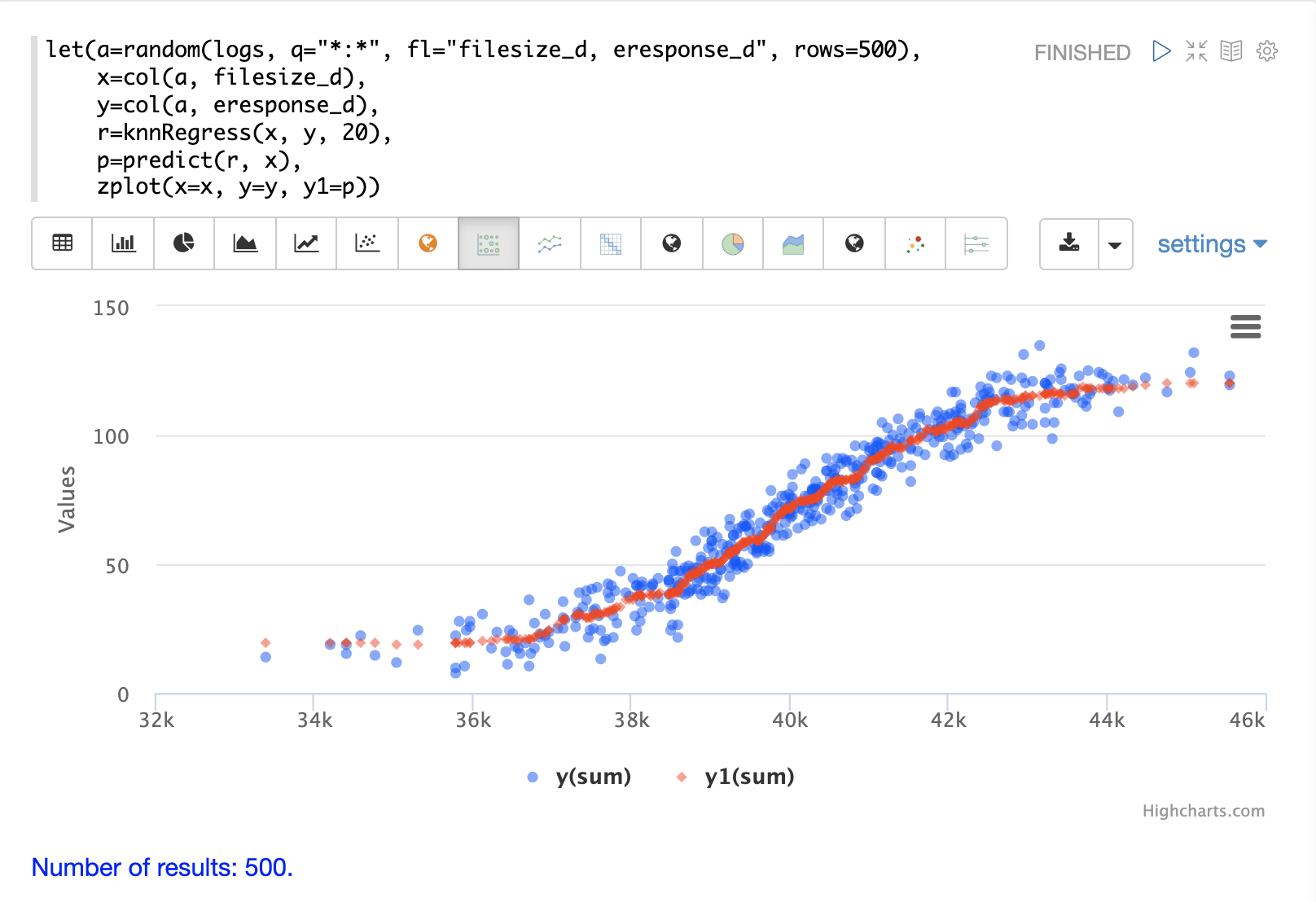
$knnRegress$

回帰プロットは、filesize_dフィールドとeresponse_dフィールドの間に非線形関係を示していることに注意してください。また、KNN回帰は散布図に非線形曲線をプロットします。K（最近傍）のサイズが大きいほど、線は滑らかになります。

多変量非線形回帰

knnRegress関数は、多変量非線形回帰にも強力で柔軟なツールです。

以下の例では、ワインの品質の分析と予測を目的としたデータベースを使用して多変量回帰を実行します。このデータベースには、ワインの品質の9つの予測因子（pH、アルコール、固定酸度、硫酸塩、密度、遊離亜硫酸、揮発性酸度、クエン酸、残留糖）を含む、約1600件のレコードが含まれています。また、3から8までの範囲の品質が各ワインに割り当てられています。

KNN回帰を使用して、予測変数の値を含むベクトルのワインの品質を予測できます。

この例では、redwineコレクションで検索を実行して、観測値のデータベース内のすべての行を返します。次に、品質フィールドと予測変数フィールドがベクトルに読み込まれ、変数に設定されます。

予測変数は行列に行として追加され、転置されるため、行列の各行には9つの予測値を持つ1つの観測値が含まれます。これは、変数obsに割り当てられた観測行列です。

次に、knnRegress関数は、品質の結果を使用して観測値を回帰します。この例ではKの値が5に設定されているため、5つの最近傍の平均品質を使用して品質を計算します。

次に、predict関数を用いて、観測セット全体の予測ベクトルを生成します。これらの予測は、観測データに対するKNN回帰の性能を判断するために使用されます。

次に、**予測**された品質から**観測**された品質を減算することで、回帰の誤差、つまり**残差**を計算します。ebeSubtract関数は、2つのベクトル間の要素ごとの減算を実行するために使用されます。

最後に、zplot関数は、**残差プロット**の視覚化のために予測と誤差をフォーマットします。

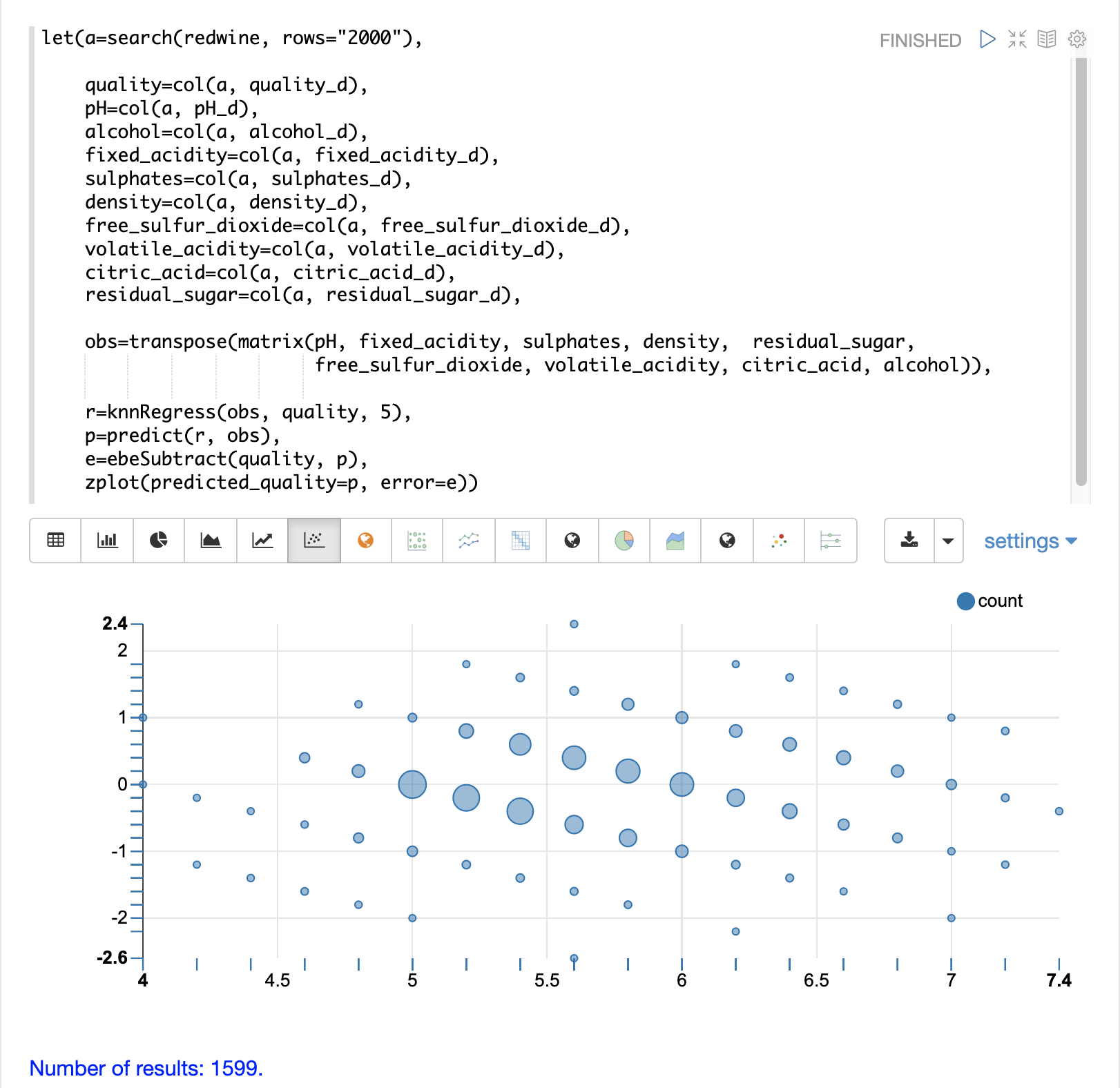
$redwine1$

残差プロットは、x軸に**予測**値、y軸に予測の**誤差**をプロットします。散布図は、誤差が予測の全範囲にわたってどのように分布しているかを示しています。

残差プロットは、トレーニングデータに対するKNN回帰の性能を理解するために解釈できます。

プロットは、予測誤差が0の上下にほぼ均等に分布していることを示しています。誤差の密度は、0に近づくにつれて増加します。バブルのサイズは、プロット内の特定の点における誤差の密度を反映しています。これにより、モデルの誤差の分布を直感的に把握できます。
プロットは、予測の範囲全体にわたる誤差の分散も視覚化します。これにより、KNN予測が予測の全範囲にわたって同様の誤差分散を持つかどうかを直感的に理解できます。

残差の分布の形状をよりよく理解するために、ヒストグラムを使用して残差を視覚化することもできます。以下の例は、上記と同じKNN回帰と、誤差の分布のプロットを示しています。

この例では、zplot関数は、11個のビンを持つヒストグラムで、残差のempiricalDistribution関数をプロットするために使用されます。

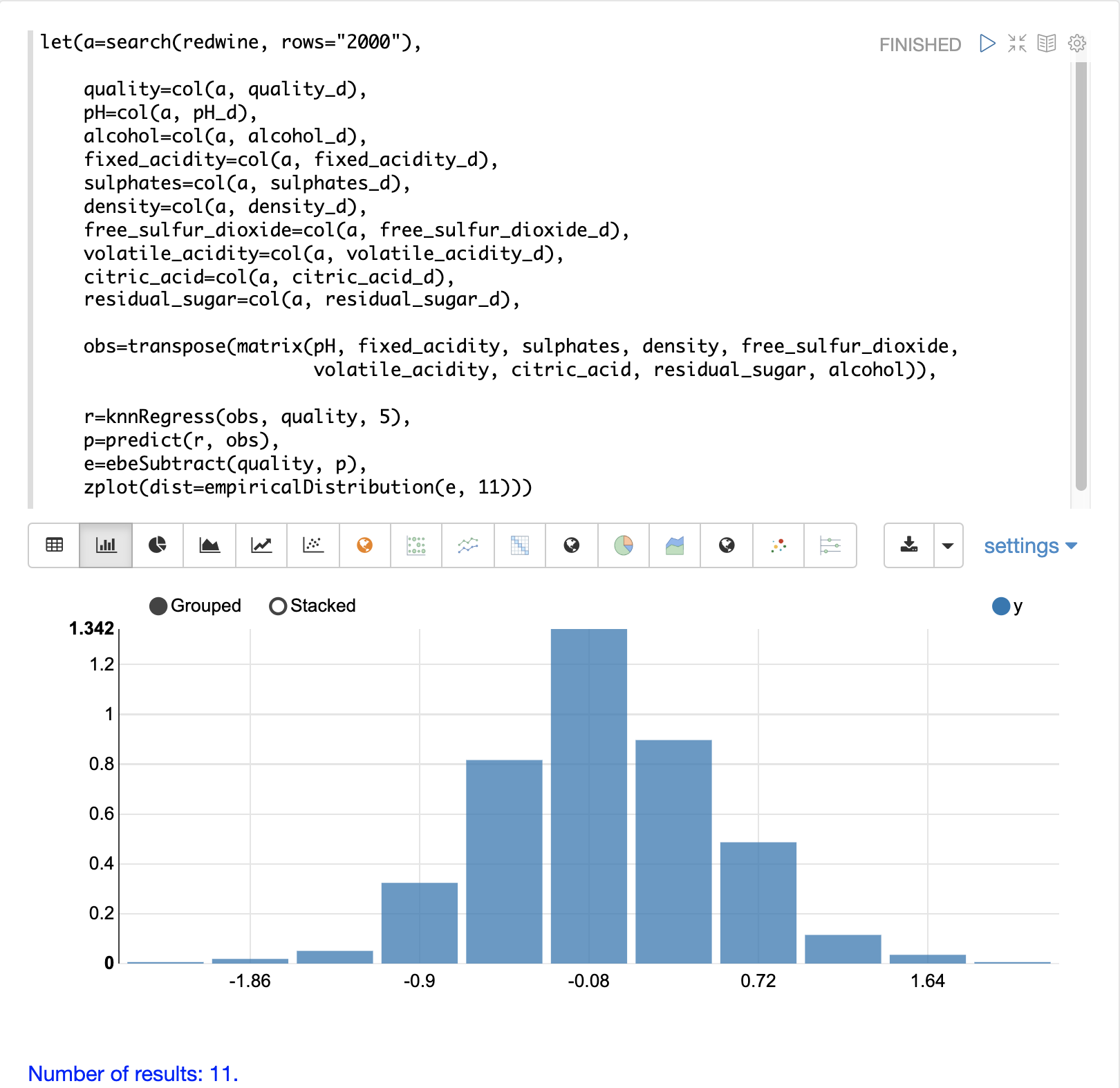
$redwine2$

誤差は、0を中心としたベルカーブに従っていることに注意してください。このプロットから、-1と1の間の予測誤差を得る確率はかなり高いことがわかります。

追加のKNN回帰パラメータ

knnRegression関数には、さまざまな回帰シナリオに適した3つの追加パラメータがあります。

関数を呼び出しに追加するだけで、回帰には任意の距離測定を使用できます。これにより、スパースベクトル（cosine）、デンスベクトル、および地理空間緯度/経度ベクトル（haversineMeters）に対する回帰分析が可能になります。

サンプル構文
```
r=knnRegress(obs, quality, 5, cosine()),
```
robust名前付きパラメータを使用して、結果の異常値に強い回帰分析を実行できます。robustパラメータを使用する場合、平均ではなく、k-最近傍の中央値の結果が使用されます。

サンプル構文
```
r=knnRegress(obs, quality, 5, robust="true"),
```
scale名前付きパラメータを使用して、予測時の観測値と検索ベクトルの列のスケーリングを行うことができます。フィーチャ列のスケールが異なり、距離計算により大きな列に過大な重みが置かれる場合、これによりKNN回帰のパフォーマンスを向上させることができます。

サンプル構文
```
r=knnRegress(obs, quality, 5, scale="true"),
```

knnSearch

knnSearch関数は、テキストの類似性に基づいて、ドキュメントのk-最近傍を返します。内部的には、knnSearch関数はSolrのMore Like Thisクエリパーサーを使用します。この機能は、検索エンジンのクエリ、用語統計、スコアリング、ランキング機能を使用して、大規模な分散インデックス上で同様のドキュメントに対する高速な最近傍検索を実行します。

この検索の結果は、直接使用したり、二次KNNベクトル検索などの機械学習操作の**候補**を提供したりできます。

以下の例は、映画レビューのデータセットに対するknnSearch関数を示しています。この検索は、review_tフィールドの類似性に基づいて、特定のドキュメントID（83e9b5b0…）と最も類似した上位50個のドキュメントを返します。mindfとmaxdfは、検索の実行に使用される用語の最小および最大ドキュメント頻度を指定します。これらのパラメータにより、高頻度用語を除外することでクエリを高速化し、ノイズ用語を検索から除外することで精度を向上させることができます。

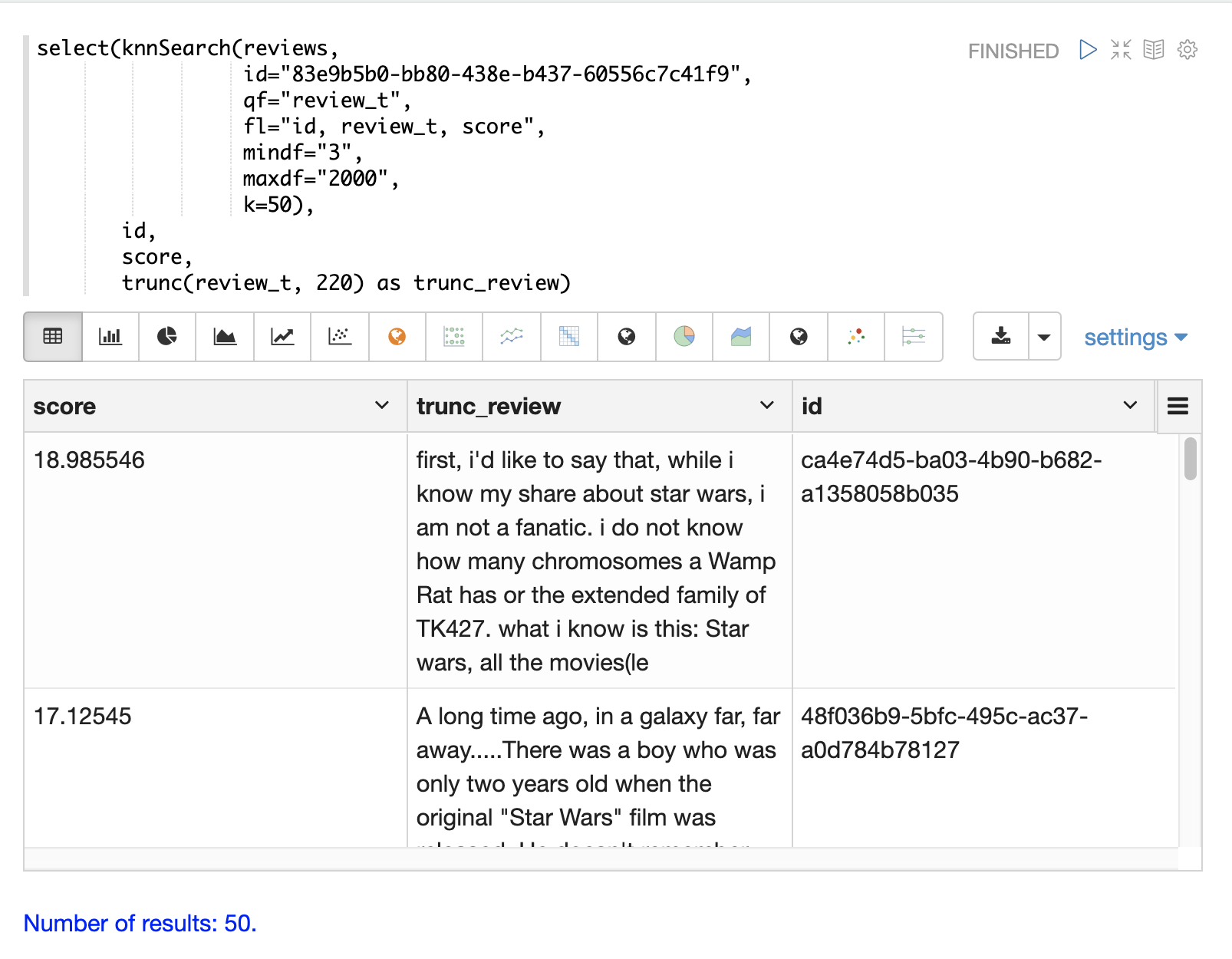
$knnSearch$

この例では、select関数を用いて、出力内のレビューを220文字に切り捨て、表で読みやすくしています。

DBSCAN

DBSCANクラスタリングは、強力な密度ベースのクラスタリングアルゴリズムであり、特に地理空間クラスタリングに適しています。DBSCANは2つのパラメータを使用して、結果セットを特定の密度を持つクラスタに絞り込みます。

eps（イプシロン）：隣接していると見なされる点間の距離を定義します。
min points：クラスタに含まれる必要のある最小の点数（クラスタとして返されるために必要です）。

2Dクラスタの可視化

zplot関数は、clustersという名前付きパラメータを使用して、2Dクラスタのプロットを直接サポートしています。

以下の例では、DBSCANクラスタリングとクラスタ可視化を使用して、NYC 311苦情データベースにおけるネズミ目撃情報の地図上の**ホットスポット**を見つけます。

この例では、random関数がnyc311コレクションからレコードのサンプルを抽出し、苦情の内容が「ネズミ目撃情報」と一致し、レコードに緯度が記入されているものを選択します。次に、緯度と経度のフィールドをベクトル化し、行列に行として追加します。行列は転置されるため、各行には単一の緯度、経度の点が含まれます。次に、dbscan関数を用いて、緯度と経度の点をクラスタリングします。例にあるdbscan関数は4つのパラメータを持つことに注意してください。

obs：緯度/経度の点の観測行列
eps：クラスタと見なされる点間の距離。例では100メートル。
min points：関数によって返されるクラスタに必要な最小の点数。例では5。
distance measure：点間の距離を決定するために使用されるオプションの距離尺度。デフォルトはユークリッド距離です。この例では、メートル単位の距離を返すhaversineMetersを使用しており、地理空間のユースケースではるかに意味があります。

最後に、zplot関数を用いて、Zeppelin-Solrで地図上にクラスタを可視化します。下の地図は、ネズミ目撃情報の高密度地域であるブルックリンの特定の地域にズームされています。

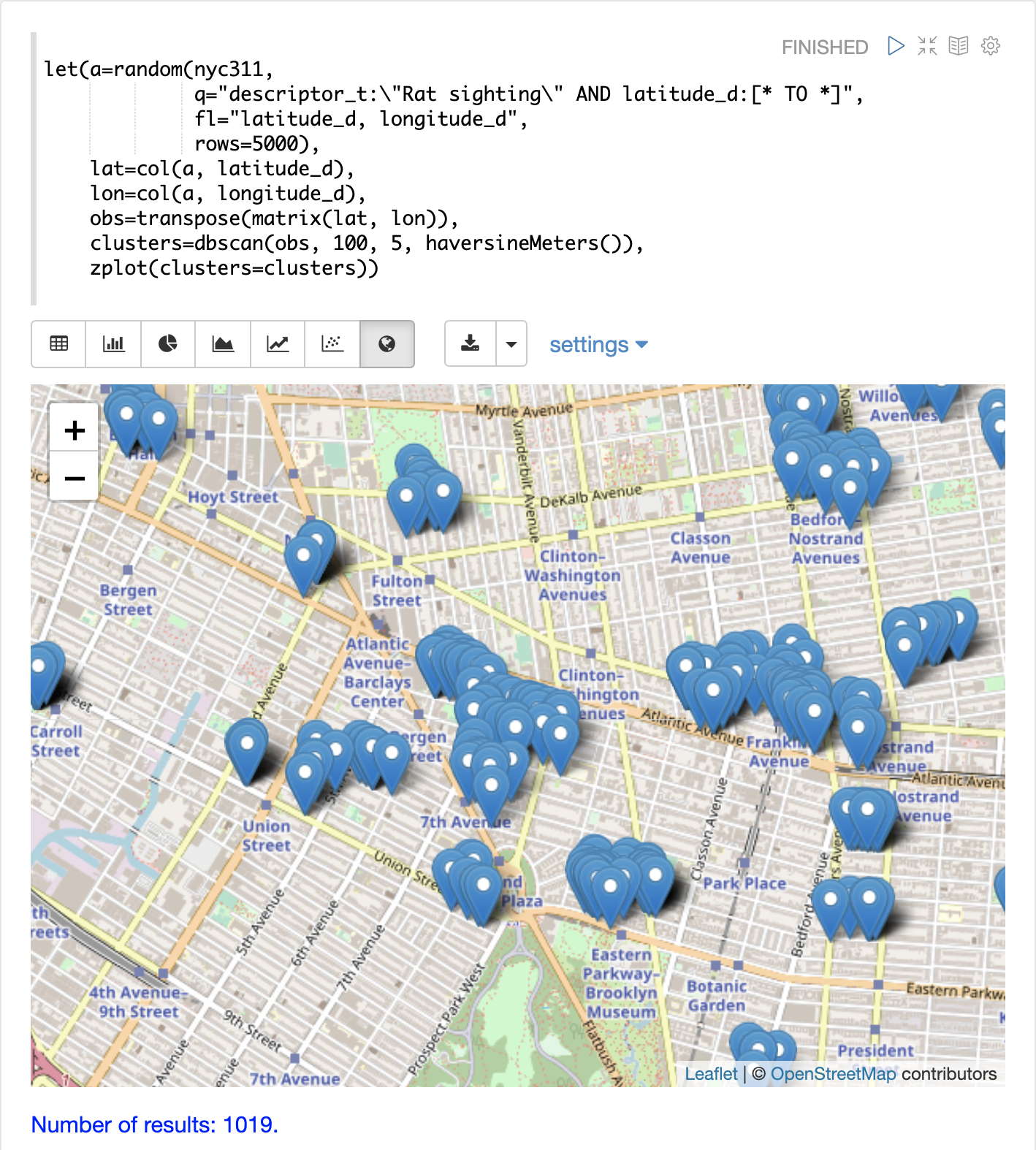
$dbscan1$

可視化では、5000個のサンプルから1019個の点しか返されていないことに注意してください。これは、クラスタの基準に合わないレコードをフィルタリングするDBSCANアルゴリズムの威力です。プロットされている点はすべて、明確に定義されたクラスタに属します。

地図の可視化をさらに拡大して、特定のクラスタの位置を調べることができます。以下の例は、高密度クラスタの領域へのズームを示しています。

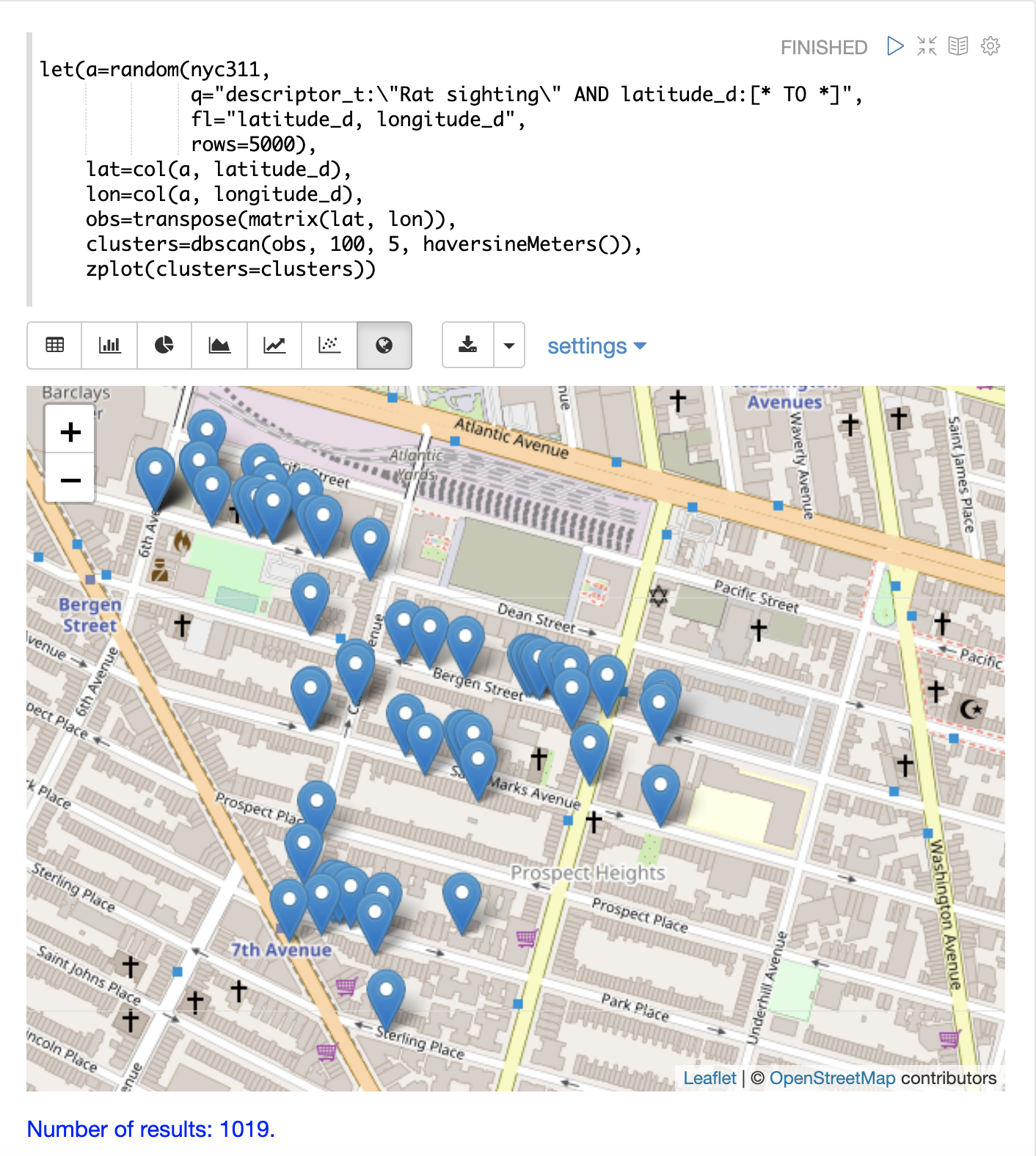
$dbscan2$

K-Meansクラスタリング

kmeans関数は、行列の行のK-Meansクラスタリングを実行します。クラスタリングが完了すると、クラスタとセントロイドを検査および可視化するための多くの便利な関数が利用できます。

クラスタリングされた散布図

この例では、再びネズミ目撃情報の2D緯度/経度点をクラスタリングします。しかし、DBSCANの例とは異なり、K-Meansクラスタリング自体はノイズ低減を実行しません。そのため、ノイズを低減するために、DBSCANの例で使用されたデータよりも小さいランダムサンプルが選択されます。

サンプリング自体が強力なノイズ低減ツールであり、クラスタ密度を視覚化するのに役立つことがわかります。これは、高密度クラスタからサンプルが抽出される確率が高く、低密度クラスタからサンプルが抽出される確率が低いためです。

この例では、random関数がnyc311（苦情データベース）コレクションから1500件のレコードのサンプルを抽出し、苦情の内容が「ネズミ目撃情報」と一致し、レコードに緯度が記入されているものを選択します。次に、緯度と経度のフィールドをベクトル化し、行列に行として追加します。行列は転置されるため、各行には単一の緯度、経度の点が含まれます。次に、kmeans関数を用いて、緯度と経度の点を21個のクラスタにクラスタリングします。最後に、zplot関数を用いて、クラスタを散布図として可視化します。

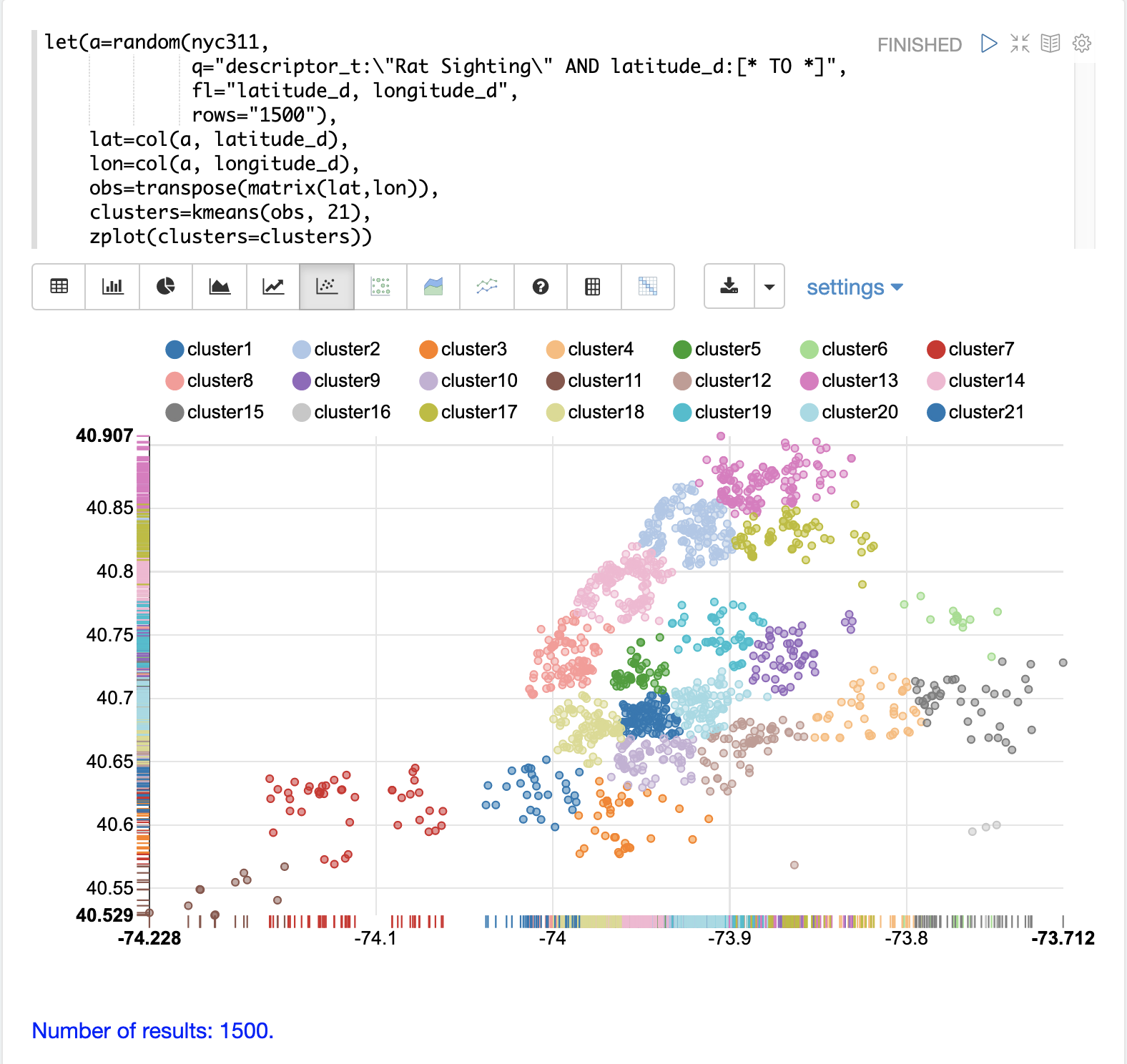
$2DCluster1$

上の散布図は、x軸に経度、y軸に緯度をとって、各緯度/経度点をユークリッド平面にプロットしたものです。プロットは十分に密集しているため、ニューヨーク市の行政区画を知っていれば、異なる行政区画の輪郭を見ることができます。

各クラスタは異なる色で表示されます。このプロットは、ニューヨーク市の5つの行政区画全体におけるネズミ目撃情報の密度に関する興味深い洞察を提供します。たとえば、cluster1を中心としたブルックリンの高密度目撃情報のクラスタと、密度が低いものの依然として高い活動を示すクラスタが周囲にあることが強調されています。

セントロイドのプロット

次に、各クラスタのセントロイドを地図上にプロットして、クラスタの中心を視覚化することができます。以下の例では、getCentroids関数を使用してクラスタからセントロイドを抽出し、セントロイドの行列を返します。

セントロイド行列には、2D緯度/経度点が含まれています。次に、colAt関数を用いて、行列からインデックスによって緯度と経度の列を抽出し、zplotでプロットすることができます。以下の地図の可視化を使用して、セントロイドを表示します。

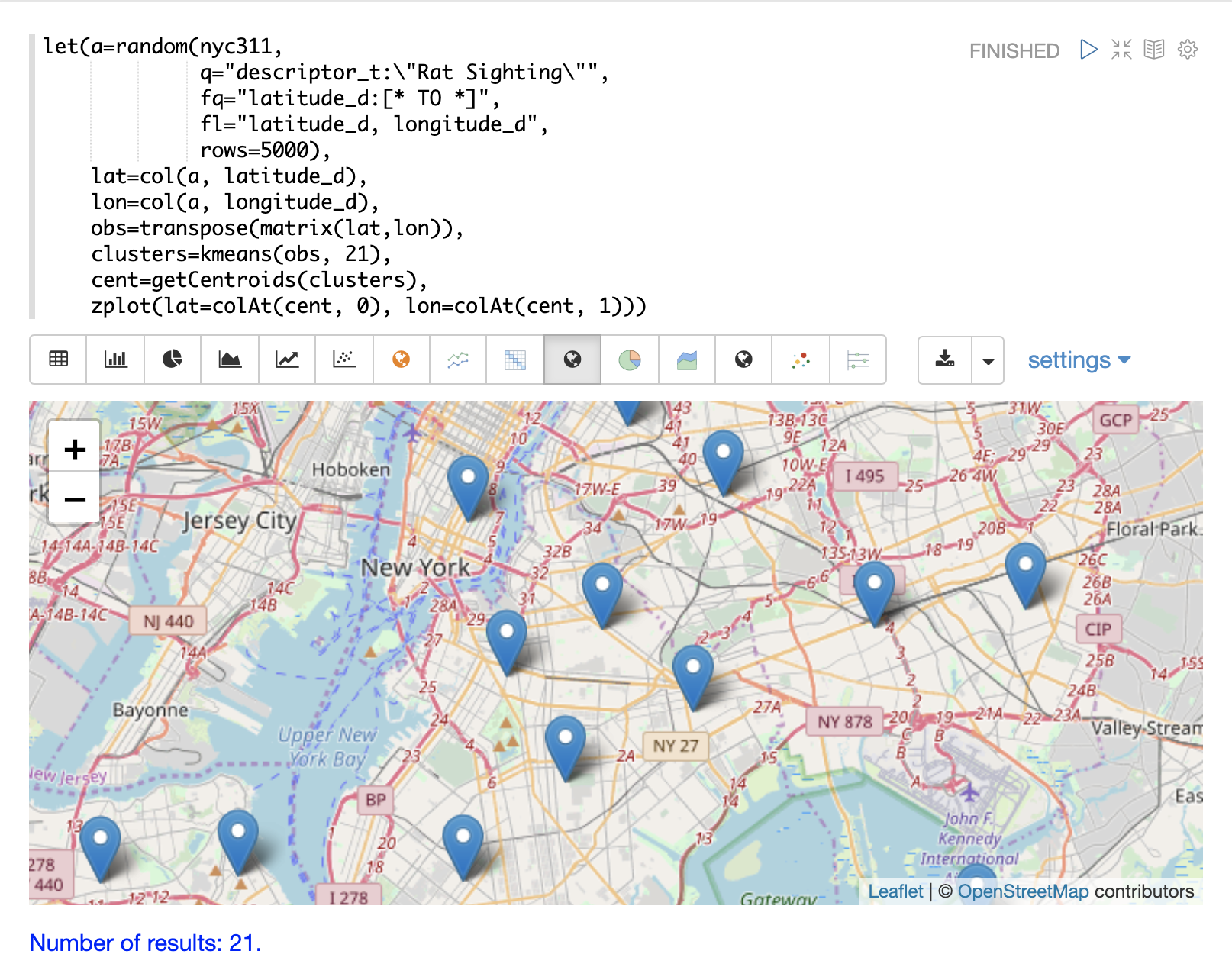
$centroidplot$

地図を拡大して、クラスタ散布図に示されている高密度領域のセントロイドを詳しく見ることができます。

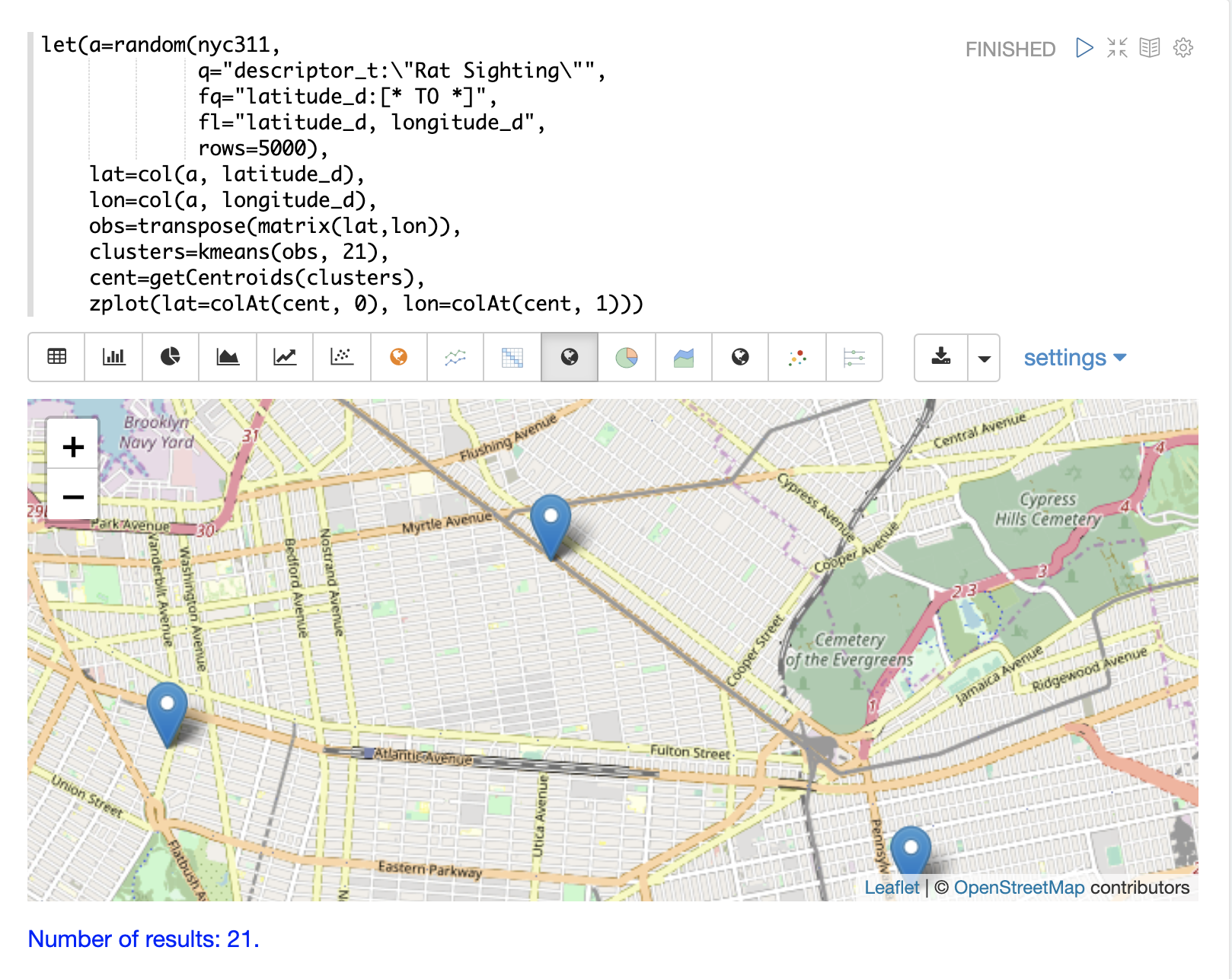
$centroidzoom$

フレーズの抽出

K-Meansクラスタリングは、各クラスタを表すために使用できるセントロイドまたは**プロトタイプ**ベクトルを生成します。この例では、セントロイドの主要な特徴を抽出して、TF-IDF用語ベクトルのクラスタの主要フレーズを表します。

以下の例はTF-IDFの*用語ベクトル*を扱っています。テキスト分析と用語ベクトルセクションでは、これらの機能について詳しく説明しています。

この例では、search関数がreview_tフィールドがフレーズ「スターウォーズ」と一致するドキュメントを返します。select関数は結果セットに対して実行され、analyze関数を適用します。この関数は、スキーマフィールドtext_bigramsにアタッチされているアナライザを使用して、review_tフィールドを再分析します。このアナライザはバイグラムを返し、termsというフィールドのドキュメントにアノテーション付けされます。

次に、termVectors関数は、termsフィールドに格納されているバイグラムからTD-IDF用語ベクトルを作成します。次に、kmeans関数を用いて、バイグラム用語ベクトルを5つのクラスタにクラスタリングします。最後に、セントロイドから上位5つの特徴が抽出されて返されます。特徴はすべて、意味的に重要なバイグラムフレーズであることに注意してください。

let(a=select(search(reviews, q="review_t:\"star wars\"", rows="500"),
             id,
             analyze(review_t, text_bigrams) as terms),
    vectors=termVectors(a, maxDocFreq=.10, minDocFreq=.03, minTermLength=13, exclude="_,br,have"),
    clusters=kmeans(vectors, 5),
    centroids=getCentroids(clusters),
    phrases=topFeatures(centroids, 5))

この式が/streamハンドラに送信されると、次のように応答します。

{
  "result-set": {
    "docs": [
      {
        "phrases": [
          [
            "empire strikes",
            "rebel alliance",
            "princess leia",
            "luke skywalker",
            "phantom menace"
          ],
          [
            "original star",
            "main characters",
            "production values",
            "anakin skywalker",
            "luke skywalker"
          ],
          [
            "carrie fisher",
            "original films",
            "harrison ford",
            "luke skywalker",
            "ian mcdiarmid"
          ],
          [
            "phantom menace",
            "original trilogy",
            "harrison ford",
            "john williams",
            "empire strikes"
          ],
          [
            "science fiction",
            "fiction films",
            "forbidden planet",
            "character development",
            "worth watching"
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 46
      }
    ]
  }
}

マルチK-Meansクラスタリング

K-Meansクラスタリングは、セントロイドの初期配置に応じて異なる結果を生成します。K-Meansは非常に高速であるため、複数の試行を実行して最適な結果を選択することができます。

multiKmeans関数は、指定された試行回数についてK-Meansクラスタリングアルゴリズムを実行し、クラスタ内分散が最も低い試行に基づいて最適な結果を選択します。

以下の例は、フレーズの抽出の例と同一ですが、kmeans関数の単一試行ではなく、15回の試行でmultiKmeansを使用している点が異なります。

let(a=select(search(reviews, q="review_t:\"star wars\"", rows="500"),
             id,
             analyze(review_t, text_bigrams) as terms),
    vectors=termVectors(a, maxDocFreq=.10, minDocFreq=.03, minTermLength=13, exclude="_,br,have"),
    clusters=multiKmeans(vectors, 5, 15),
    centroids=getCentroids(clusters),
    phrases=topFeatures(centroids, 5))

この式は次の応答を返します。

{
  "result-set": {
    "docs": [
      {
        "phrases": [
          [
            "science fiction",
            "original star",
            "production values",
            "fiction films",
            "forbidden planet"
          ],
          [
            "empire strikes",
            "princess leia",
            "luke skywalker",
            "phantom menace"
          ],
          [
            "carrie fisher",
            "harrison ford",
            "luke skywalker",
            "empire strikes",
            "original films"
          ],
          [
            "phantom menace",
            "original trilogy",
            "harrison ford",
            "character development",
            "john williams"
          ],
          [
            "rebel alliance",
            "empire strikes",
            "princess leia",
            "original trilogy",
            "luke skywalker"
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 84
      }
    ]
  }
}

ファジィK-Meansクラスタリング

fuzzyKmeans関数は、ベクトルを複数のクラスタに割り当てることができるソフトクラスタリングアルゴリズムです。fuzzinessパラメータは1と2の間の値であり、クラスタ割り当てをどの程度ファジィにするかを決定します。

クラスタリングが実行された後、クラスタリング結果に対してgetMembershipMatrix関数を呼び出して、各ベクトルのクラスタメンバーシップの確率を示す行列を返すことができます。この行列を使用して、クラスタ間の関係を理解することができます。

以下の例では、fuzzyKmeansを使用して、「スターウォーズ」というフレーズに一致する映画レビューをクラスタリングします。しかし、クラスタやセントロイドを見る代わりに、getMembershipMatrixを使用して各ドキュメントのメンバーシップ確率を返します。メンバーシップ行列は、クラスタリングされた各ベクトルに対応する行で構成されています。行列には、各クラスタに対応する列があります。行列の値には、特定のベクトルが特定のクラスタに属する確率が含まれています。

この例では、distance関数を用いて、メンバーシップ行列の列から**距離行列**を作成します。次に、zplot関数を用いて、距離行列をヒートマップとして可視化します。

この例では、cluster1とcluster5のクラスタ間の距離が最も短くなっています。両方のクラスタの特徴をさらに分析して、cluster1とcluster5の関係を理解することができます。

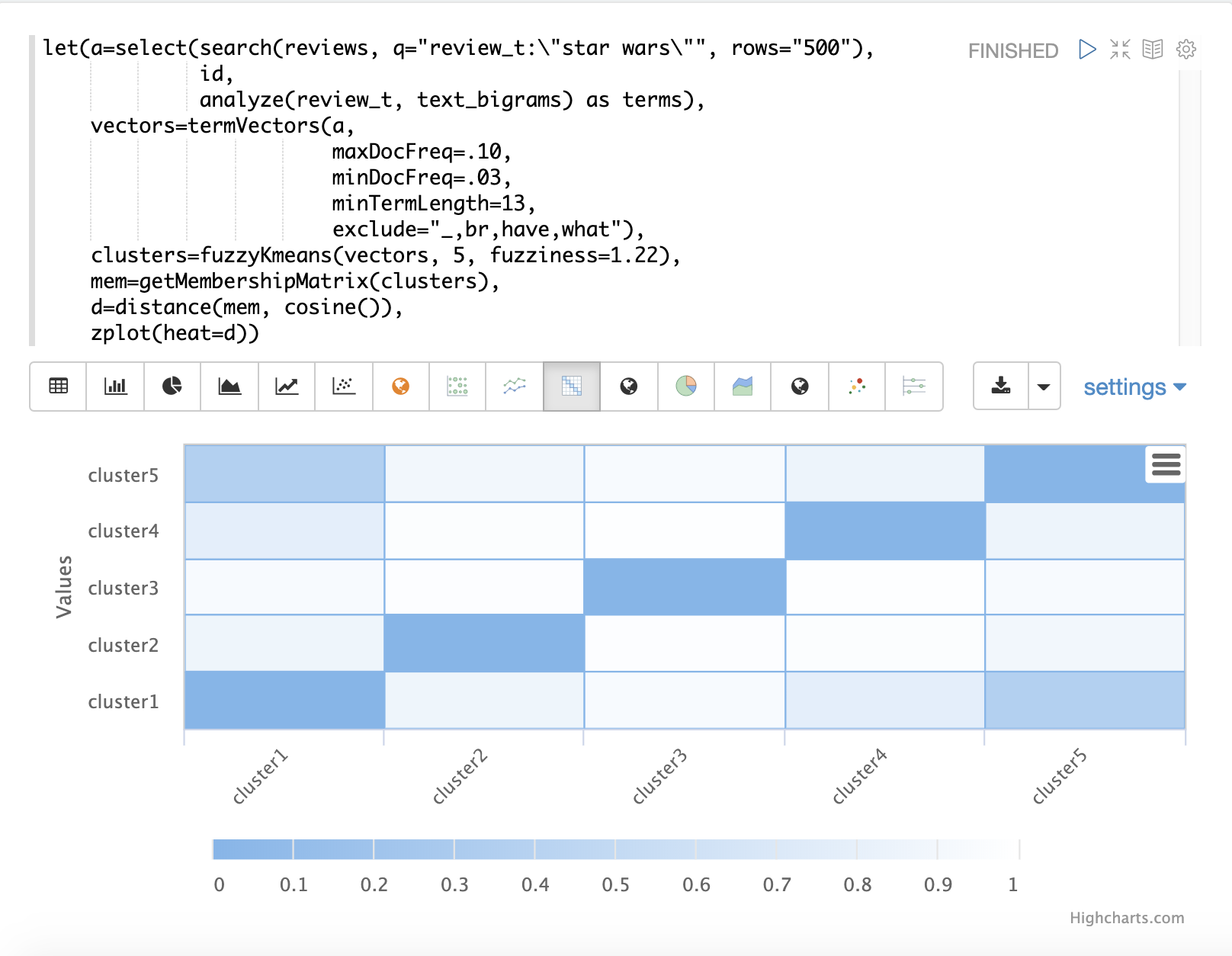
$fuzzyk$

ヒートマップは、距離が短くなるにつれて色の濃度が高くなるように設定されています。

特徴スケーリング

機械学習操作を実行する前に、特徴ベクトルを同じスケールで比較できるように、特徴ベクトルをスケーリングすることがよく必要です。

以下のすべてのスケーリング関数は、ベクトルと行列に対して動作します。行列に対して動作する場合、行列の行がスケーリングされます。

最小/最大スケーリング

minMaxScale関数は、ベクトルまたは行列を最小値と最大値の間にスケーリングします。デフォルトでは、最小値/最大値が提供されない場合、0と1の間にスケーリングされます。

以下は、振幅が1の正弦波を、-5と5の間にスケーリングする前と後のプロットです。

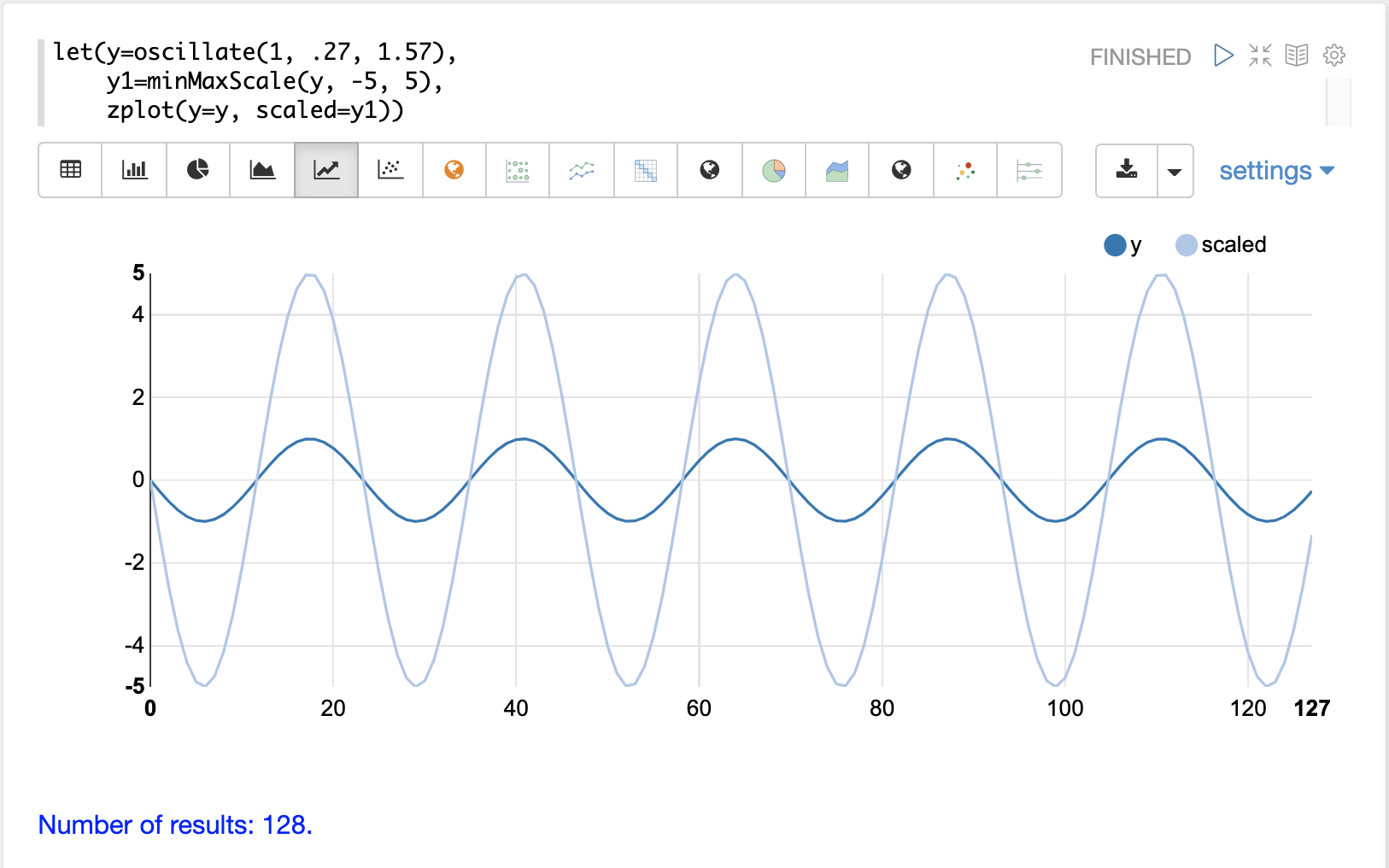
$minmaxscale$

以下は、0と1の間に行列を最小/最大スケーリングする簡単な例です。同じスケールにすると、ベクトルが同じになることに注意してください。

let(a=array(20, 30, 40, 50),
    b=array(200, 300, 400, 500),
    c=matrix(a, b),
    d=minMaxScale(c))

この式が/streamハンドラに送信されると、次のように応答します。

{
  "result-set": {
    "docs": [
      {
        "d": [
          [
            0,
            0.3333333333333333,
            0.6666666666666666,
            1
          ],
          [
            0,
            0.3333333333333333,
            0.6666666666666666,
            1
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

標準化

standardize関数は、平均が0、標準偏差が1になるようにベクトルをスケーリングします。

以下は、振幅が1の正弦波を標準化の前と後のプロットです。

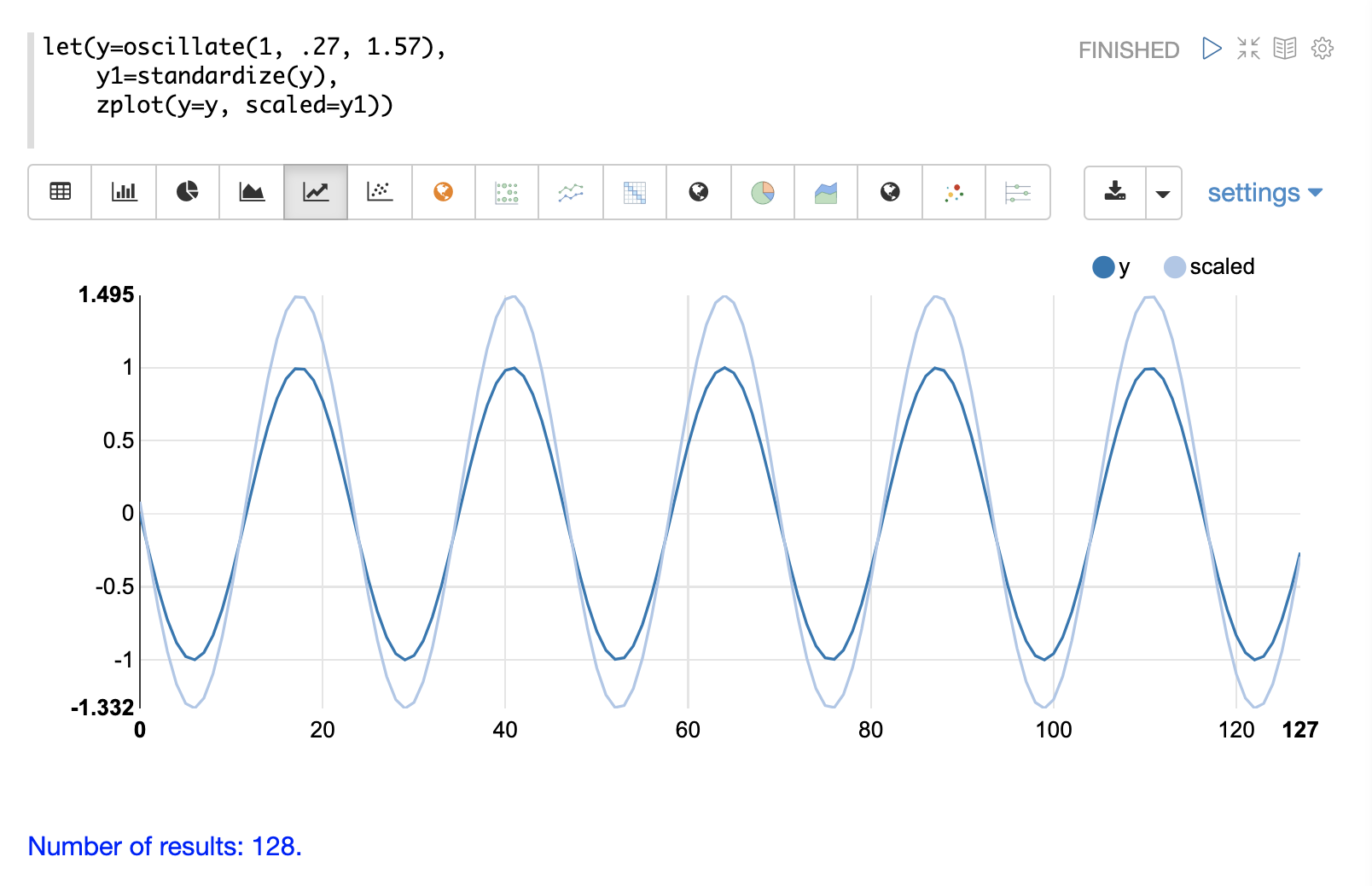
$standardize$

以下は、標準化された行列の簡単な例です。同じスケールにすると、ベクトルが同じになることに注意してください。

let(a=array(20, 30, 40, 50),
    b=array(200, 300, 400, 500),
    c=matrix(a, b),
    d=standardize(c))

この式が/streamハンドラに送信されると、次のように応答します。

{
  "result-set": {
    "docs": [
      {
        "d": [
          [
            -1.161895003862225,
            -0.3872983346207417,
            0.3872983346207417,
            1.161895003862225
          ],
          [
            -1.1618950038622249,
            -0.38729833462074165,
            0.38729833462074165,
            1.1618950038622249
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 17
      }
    ]
  }
}

単位ベクトル

unitize関数は、ベクトルを大きさ1にスケーリングします。大きさ1のベクトルは単位ベクトルとして知られています。ベクトル演算が大きさではなくベクトルの向きを扱う場合は、単位ベクトルが優先されます。

以下は、振幅が1の正弦波を単位化の前と後のプロットです。

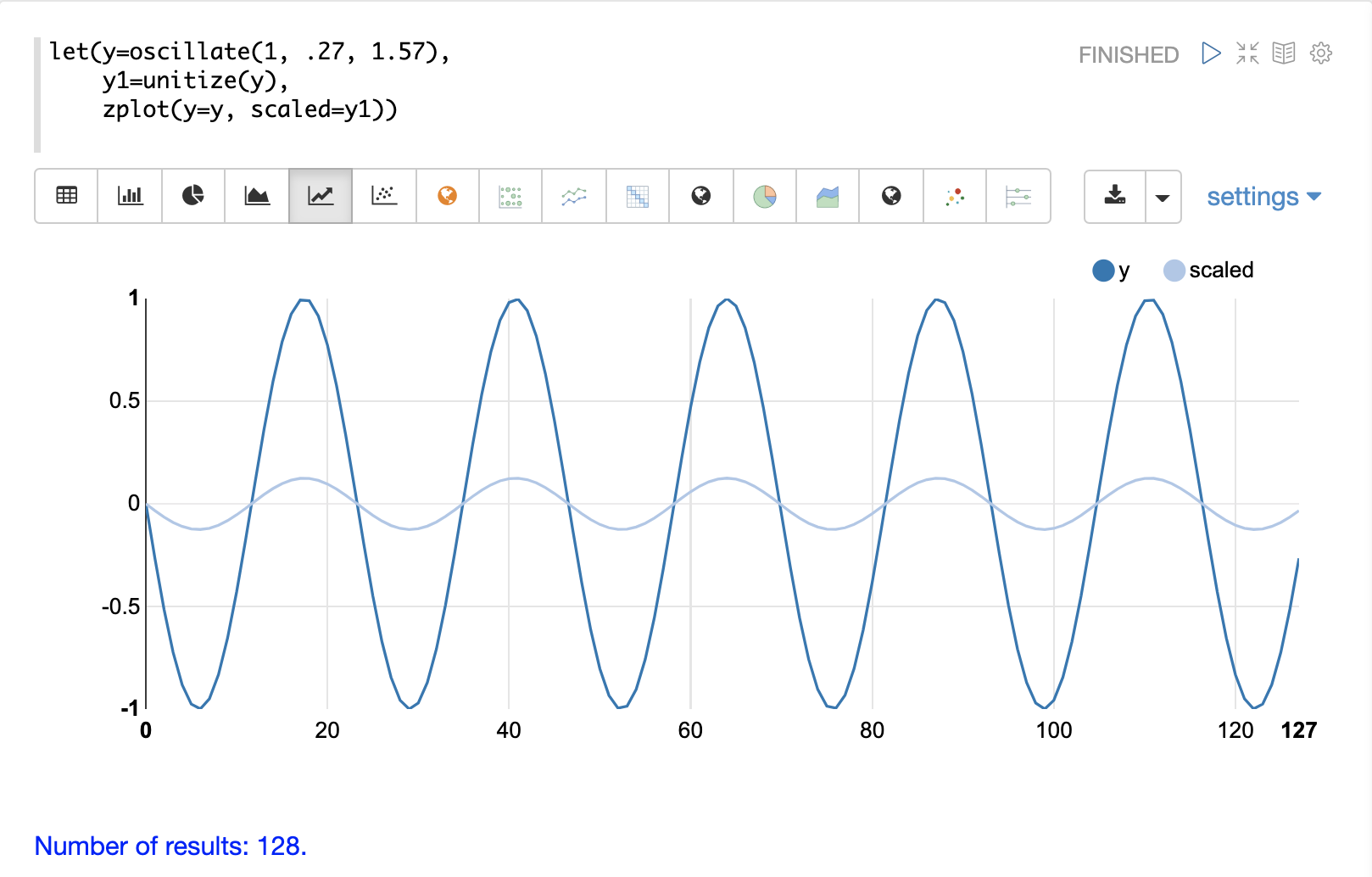
$unitize$

以下は、単位化された行列の簡単な例です。同じスケールにすると、ベクトルが同じになることに注意してください。

let(a=array(20, 30, 40, 50),
    b=array(200, 300, 400, 500),
    c=matrix(a, b),
    d=unitize(c))

この式が/streamハンドラに送信されると、次のように応答します。

{
  "result-set": {
    "docs": [
      {
        "d": [
          [
            0.2721655269759087,
            0.40824829046386296,
            0.5443310539518174,
            0.6804138174397716
          ],
          [
            0.2721655269759087,
            0.4082482904638631,
            0.5443310539518174,
            0.6804138174397717
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 6
      }
    ]
  }
}