補間、微分、積分
このセクションでは、補間と数値計算のための相互に関連する数式を探ります。
補間
補間は、既知の制御点のセットの間で新しいデータポイントを構築するために使用されます。新しいデータポイントを予測する機能により、制御点によって定義された曲線に沿ったサンプリングが可能になります。
以下に説明するすべての補間関数は、サンプリング機能を利用する他の関数に渡すことができる補間関数を返します。
補間関数が直接返された場合、各制御点の予測を含む配列が返されます。これは、最初に制御点を平滑化してから、平滑化された点を補間するloess補間の場合に役立ちます。他のすべての補間関数は、補間が元の制御点を通る曲線を予測するため、元の制御点を単純に返します。
補間にはさまざまなアルゴリズムがあり、曲線に沿って異なる予測が行われます。数式ライブラリは現在、次の補間関数をサポートしています。
-
lerp: 線形補間は、各制御点を通る点と制御点間を直線で結ぶ点を予測します。 -
spline: スプライン補間は、各制御点を通る点と制御点間を滑らかな曲線で結ぶ点を予測します。 -
akima: Akimaスプライン補間はスプライン補間に似ていますが、外れ値に対して安定しています。 -
loess: Loess補間は、最初に非線形ローカル回帰を実行して元の制御点を平滑化します。次に、スプラインを使用して平滑化された制御点を補間します。
曲線に沿ったサンプリング
補間をより良く理解する方法の1つは、曲線に沿ってサンプリングすることが何を意味するのかを視覚化することです。以下の例では、特定のx軸範囲の間の曲線をサンプリングすることにより、曲線の特定の領域を拡大します。

上記の視覚化では、最初にx軸とy軸の点を持つ2つの配列を作成します。x軸が0から9の範囲であることに注意してください。次に、akima、spline、lerp関数をベクトルに適用して、3つの補間関数を作成します。
次に、0から3の一様分布から500個のランダムなサンプルが抽出されます。これらは、0から3の間の新しいズームインされたx軸の点です。曲線上の特定の領域をサンプリングしていることに注意してください。
次に、predict関数を使用して、サンプリングされたx軸に対して、3つの補間関数すべてでy軸の点を予測します。最後に、3つの予測ベクトルすべてが、サンプリングされたx軸の点とともにプロットされます。
赤い線はlerp補間、青い線はakima、紫色の線はspline補間です。それぞれが制御点の間で異なる曲線を作成していることがわかります。
平滑化補間
loess関数は平滑化補間器です。つまり、元の制御点を通る関数を導出するのではなく、loess関数は元の制御点を平滑化する関数を返します。
局所回帰として知られる手法が、平滑化された曲線を計算するために使用されます。局所回帰の近傍のサイズを調整して、新しい曲線が元の制御点にどれだけ適合するかを制御できます。
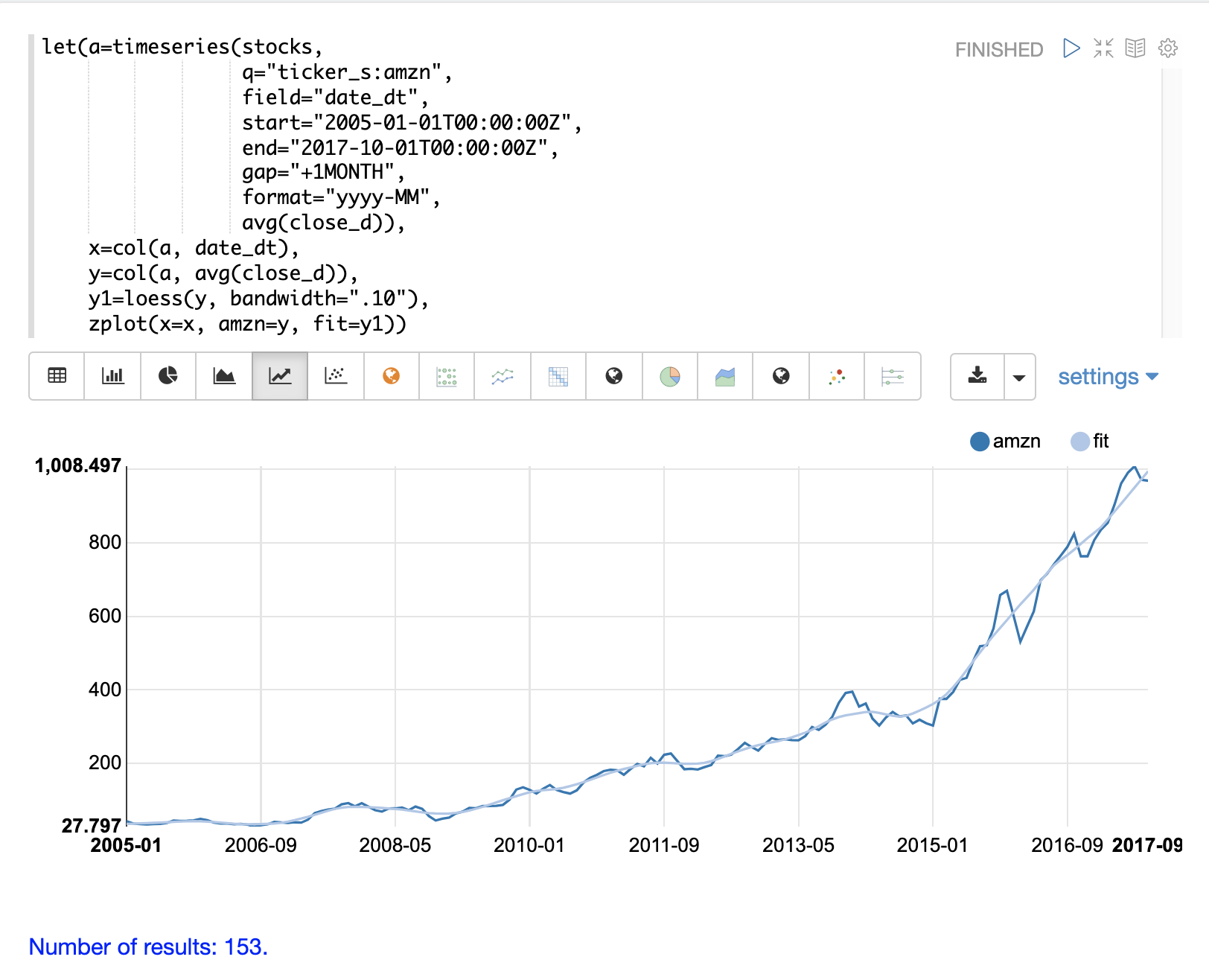
loess関数には、x軸とy軸が渡され、データに滑らかな曲線を当てはめます。単一の配列のみが提供された場合は、y軸として扱われ、x軸のシーケンスが生成されます。
以下の例は、loess関数を使用して月次時系列をモデル化する方法を示しています。この例では、timeseries関数を使用して、株式ティッカーAMZNの平均終値の月次時系列を生成します。時系列のdate_dtフィールドとavg(close_d)フィールドはベクトル化され、変数xとyに格納されます。次に、平均終値を含むyベクトルにloess関数が適用されます。bandwidthという名前のパラメーターは、局所回帰を計算するために使用されるデータセットのパーセンテージを指定します。loess関数は、平滑化されたデータポイントの適合モデルを返します。
次に、zplot関数を使用して、x、y、y1変数をプロットします。
微分
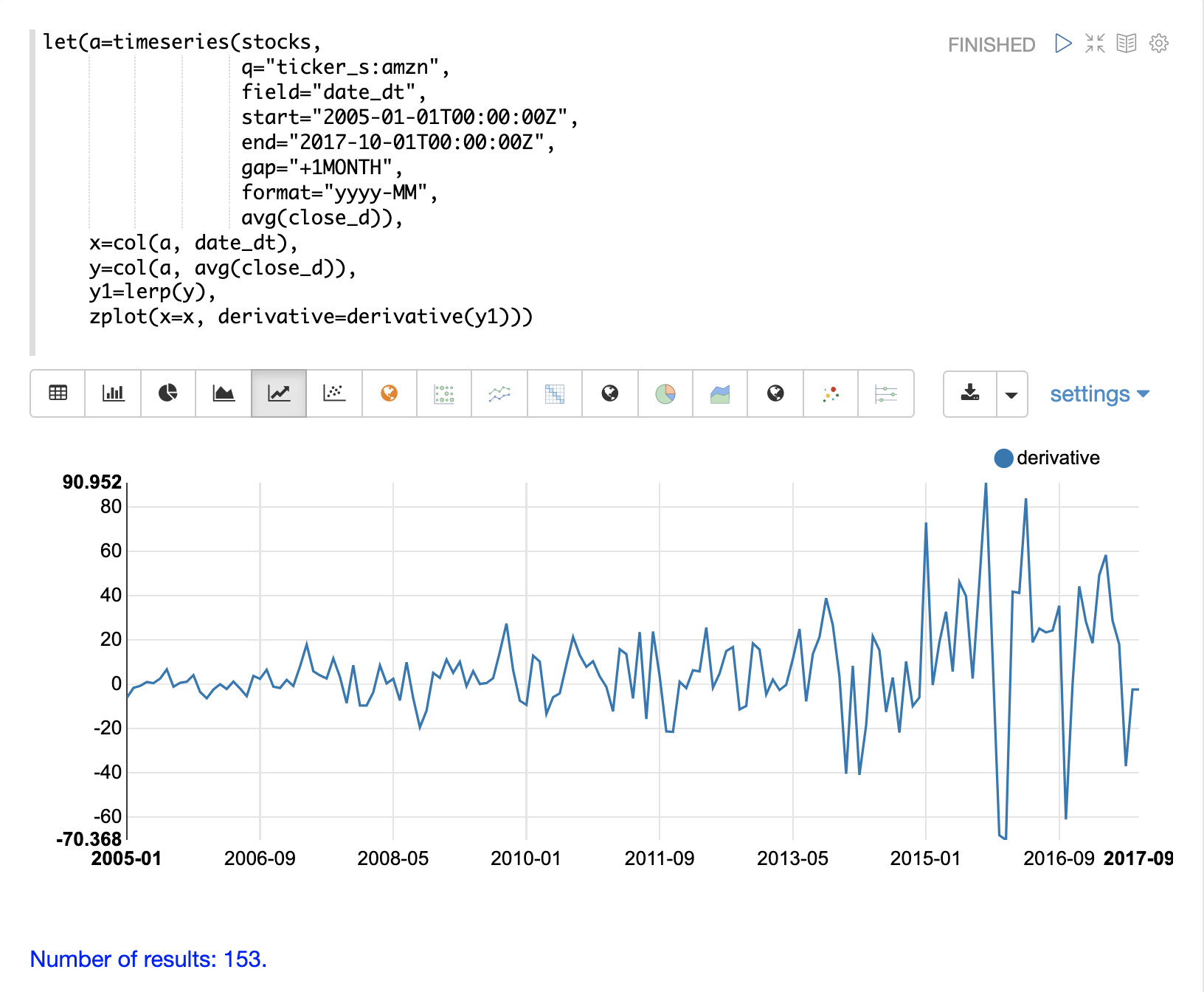
関数の微分は、x値の変化率に対するy値の変化率を測定します。
derivative関数は、上記で説明した補間関数のいずれについても微分を計算できます。各補間関数は、その関数の特性に一致する異なる微分を生成します。
一次微分(速度)
簡単な例は、derivative関数を使用して変化率または速度を計算する方法を示しています。
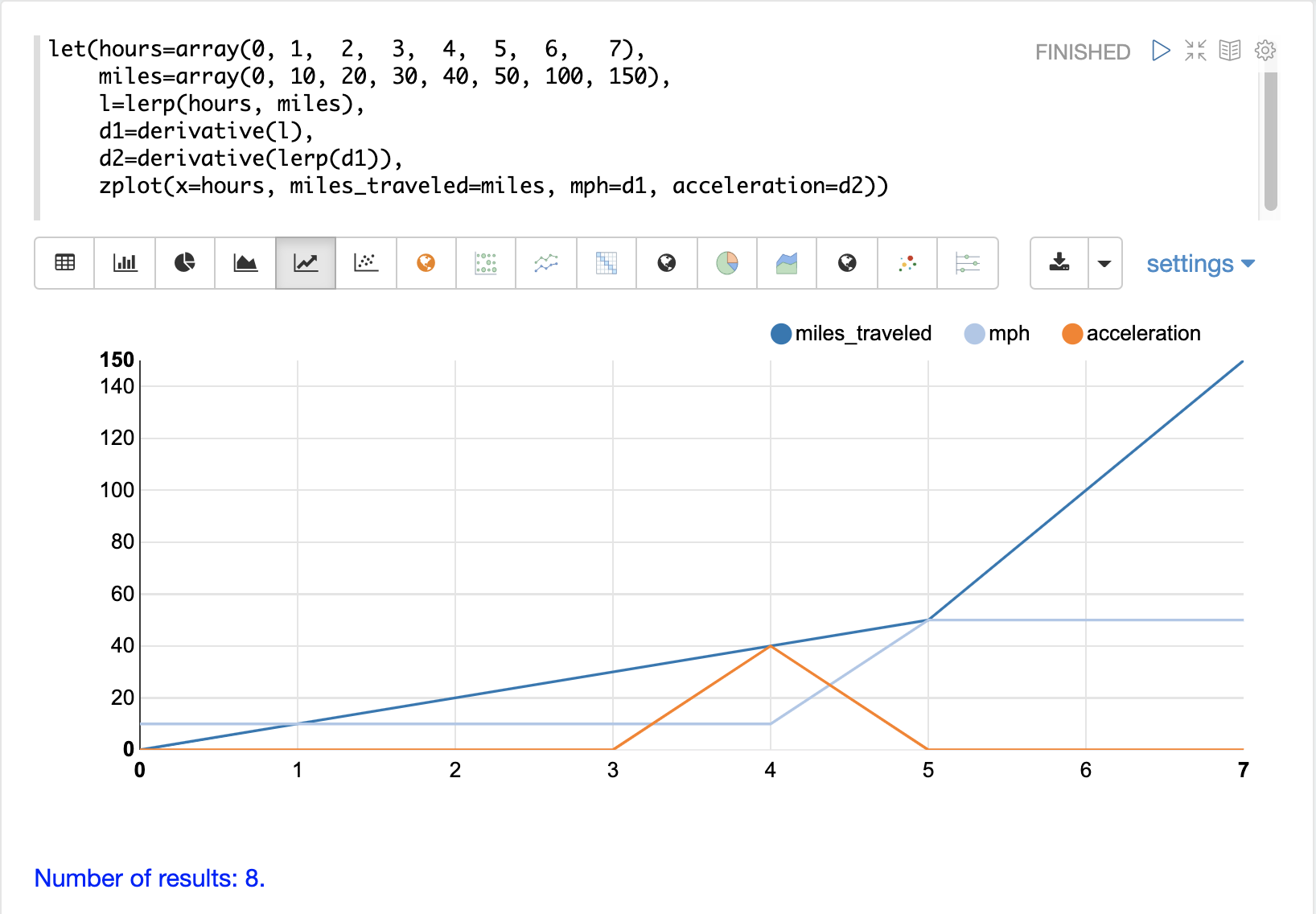
この例では、時間と移動距離を表す2つのベクトルが作成されます。次に、lerp関数を使用して、hoursベクトルとmilesベクトルの線形補間を作成します。次に、derivative関数が線形補間に適用されます。次に、zplotを使用して、x軸にhoursを、y軸にmilesをプロットし、各x軸ポイントでのmphとしてderivativeをプロットします。
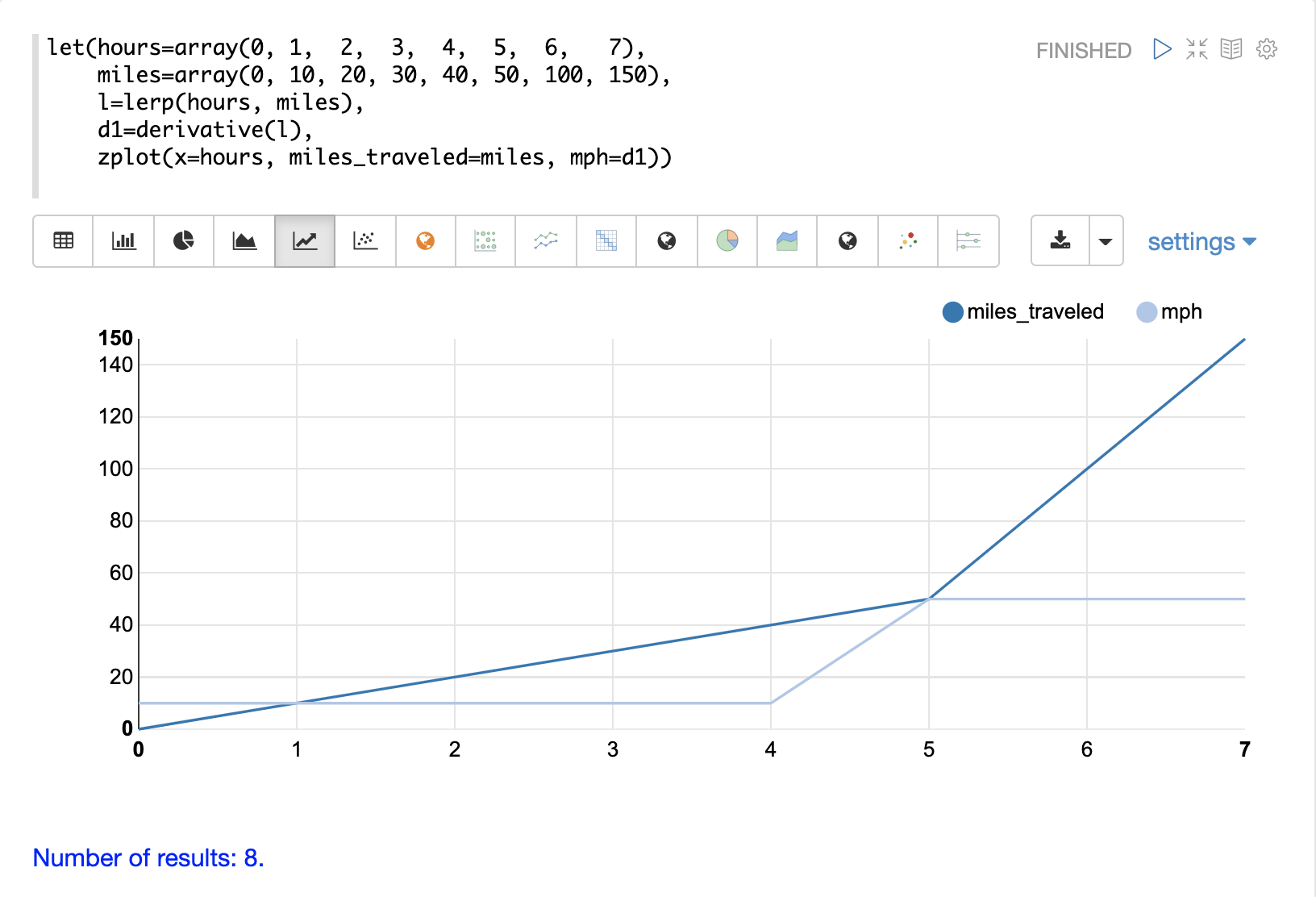
miles_traveled線は、5時間目までは傾きが10であり、その後傾きが50に変化することに注意してください。mph線(微分)は、miles_traveled線の速度を視覚化します。
また、微分は、ある点から次の点への即時の変化を示す直線に沿って計算されることにも注意してください。これは、線形補間(lerp)が補間関数として使用されているためです。splineまたはakima関数が使用されていた場合は、丸みを帯びた曲線を持つ微分が生成されたはずです。
積分
積分は、曲線の下の体積の尺度です。integral関数は、曲線の累積積分、または補間された曲線の特定の範囲の積分を計算します。derivative関数と同様に、integral関数は補間関数に対して動作します。
単一積分
integral関数にstartとendの範囲が渡された場合、その特定の範囲内の曲線下の体積を計算します。
以下の例では、integral関数は曲線全体の範囲(0から10まで)の積分を計算します。integral関数には補間された曲線と開始範囲と終了範囲が渡され、範囲の積分が返されることに注意してください。
let(x=array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20),
y=array(0, 1, 2, 3, 4, 5.7, 6, 7, 7, 7,6, 7, 7, 7, 6, 5, 5, 3, 2, 1, 0),
curve=loess(x, y, bandwidth=.3),
integral=integral(curve, 0, 10))この式が/streamハンドラーに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"integral": 45.300912584519914
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}累積積分プロット
integral関数に単一の補間曲線が渡されると、曲線の累積積分のベクトルが返されます。累積積分ベクトルには、各x軸ポイントの累積積分計算が含まれています。累積積分は、各x軸ポイントと最初のx軸ポイントの間の範囲の積分を取ることによって計算されます。上記の例では、次のような積分のベクトルを計算することを意味します。
let(x=array(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20),
y=array(0, 1, 2, 3, 4, 5.7, 6, 7, 7, 7,6, 7, 7, 7, 6, 5, 5, 3, 2, 1, 0),
curve=loess(x, y, bandwidth=.3),
integrals=array(0, integral(curve, 0, 1), integral(curve, 0, 2), integral(curve, 0, 3), ...)累積積分のプロットは、曲線の下の累積ボリュームが各x軸ポイントの下にどれだけあるかを視覚化します。
以下の例は、timeseries関数によって生成された時系列の累積積分プロットを示しています。この例では、株式ティッカーamznの平均終値の月次時系列が生成されます。avg(close)列はベクトル化され、splineを使用して補間されます。
次に、zplot関数を使用して、時系列の累積積分をプロットします。
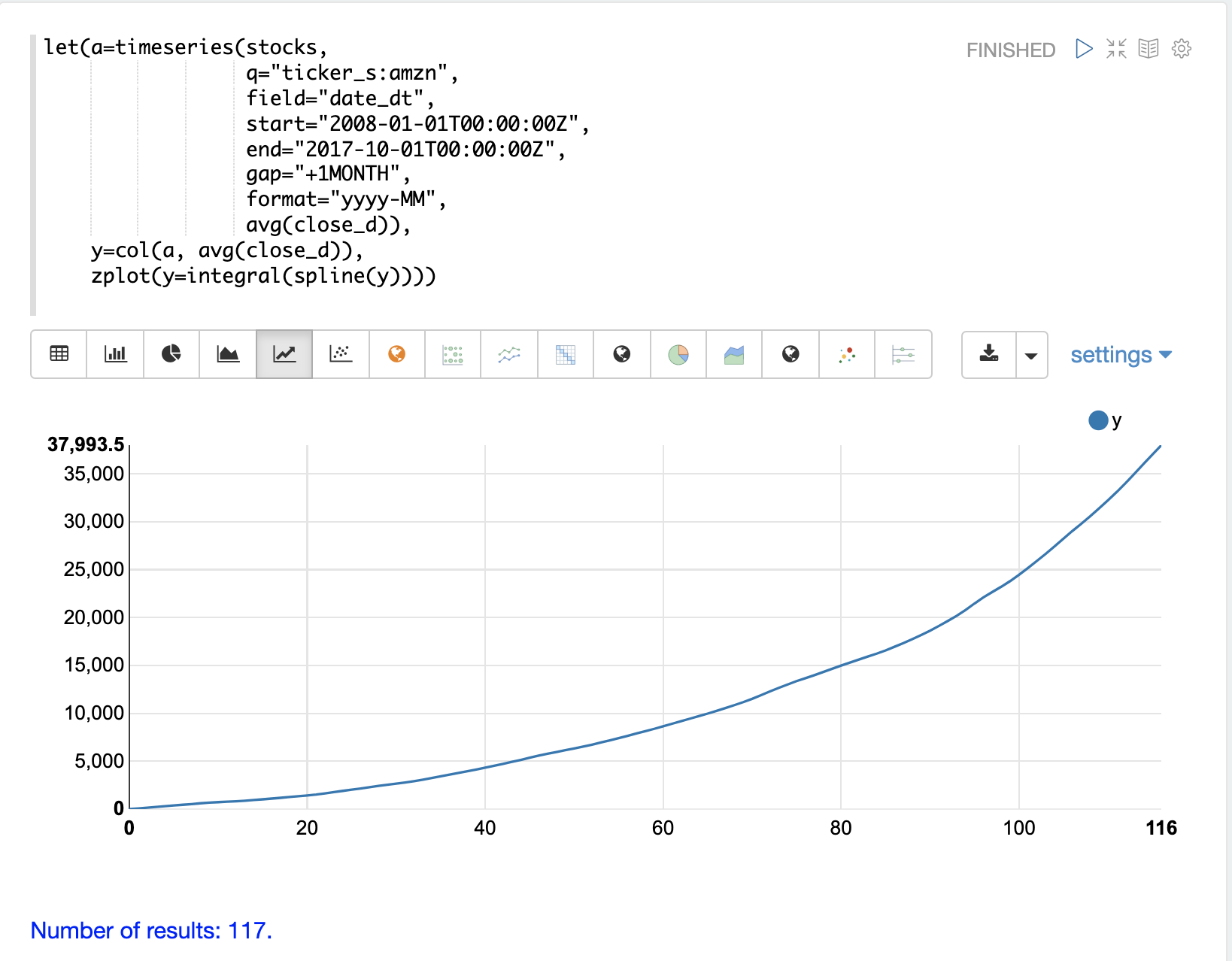
上記のプロットは、AMZNの株価が時間の経過とともに変化するにつれて、曲線の下の体積を視覚化します。このプロットは累積的であるため、時間の経過とともに同じままの株価時系列の下の体積は、正の線形勾配を持ちます。株価が上昇している株式は凹形状になり、株価が下落している株式は凸形状になります。
この特定の例では、積分プロットは時間の経過とともにますます凹になり、株価の上昇が加速していることを示しています。
双三次スプライン
bicubicSpline関数は、データのグリッド内の任意の位置で値を補間および予測するために使用できます。
簡単な例でこれがより明確になります。
let(years=array(1998, 2000, 2002, 2004, 2006),
floors=array(1, 5, 9, 13, 17, 19),
prices = matrix(array(300000, 320000, 330000, 350000, 360000, 370000),
array(320000, 330000, 340000, 350000, 365000, 380000),
array(400000, 410000, 415000, 425000, 430000, 440000),
array(410000, 420000, 425000, 435000, 445000, 450000),
array(420000, 430000, 435000, 445000, 450000, 470000)),
bspline=bicubicSpline(years, floors, prices),
prediction=predict(bspline, 2003, 8))この例では、双三次スプラインを使用して不動産データの行列を補間します。行列の各行は特定のyearsを表します。行列の各列は、建物のfloorsを表します。数値のグリッドは、各年と階のマンションの平均販売価格です。たとえば、2002年では、9階の平均販売価格は415000(3行3列)でした。
次に、bicubicSpline関数を使用してグリッドを補間し、predict関数を使用して、2003年の8階の値を予測します。行列には、2003年の8階のデータポイントが含まれていないことに注意してください。bicubicSpline関数は、行列内の周囲のデータに基づいてそのデータポイントを作成します。
{
"result-set": {
"docs": [
{
"prediction": 418279.5009328358
},
{
"EOF": true,
"RESPONSE_TIME": 0
}
]
}
}