線形回帰
数式ライブラリは、単純な線形回帰と多変量線形回帰をサポートしています。
単純線形回帰
regress 関数は、2 つの確率変数間の線形回帰モデルを構築するために使用されます。サンプルの観測値は、2 つの数値配列で提供されます。最初の数値配列は独立変数であり、2 番目の配列は従属変数です。
以下の例では、random 関数は、フィールド filesize_d と response_d をそれぞれ含む 50000 個のランダムサンプルを選択します。2 つのフィールドはベクトル化され、変数 x と y に格納されます。次に、regress 関数が 2 つの数値配列に対して回帰分析を実行します。
regress 関数は、回帰分析の結果を含む単一のタプルを返します。
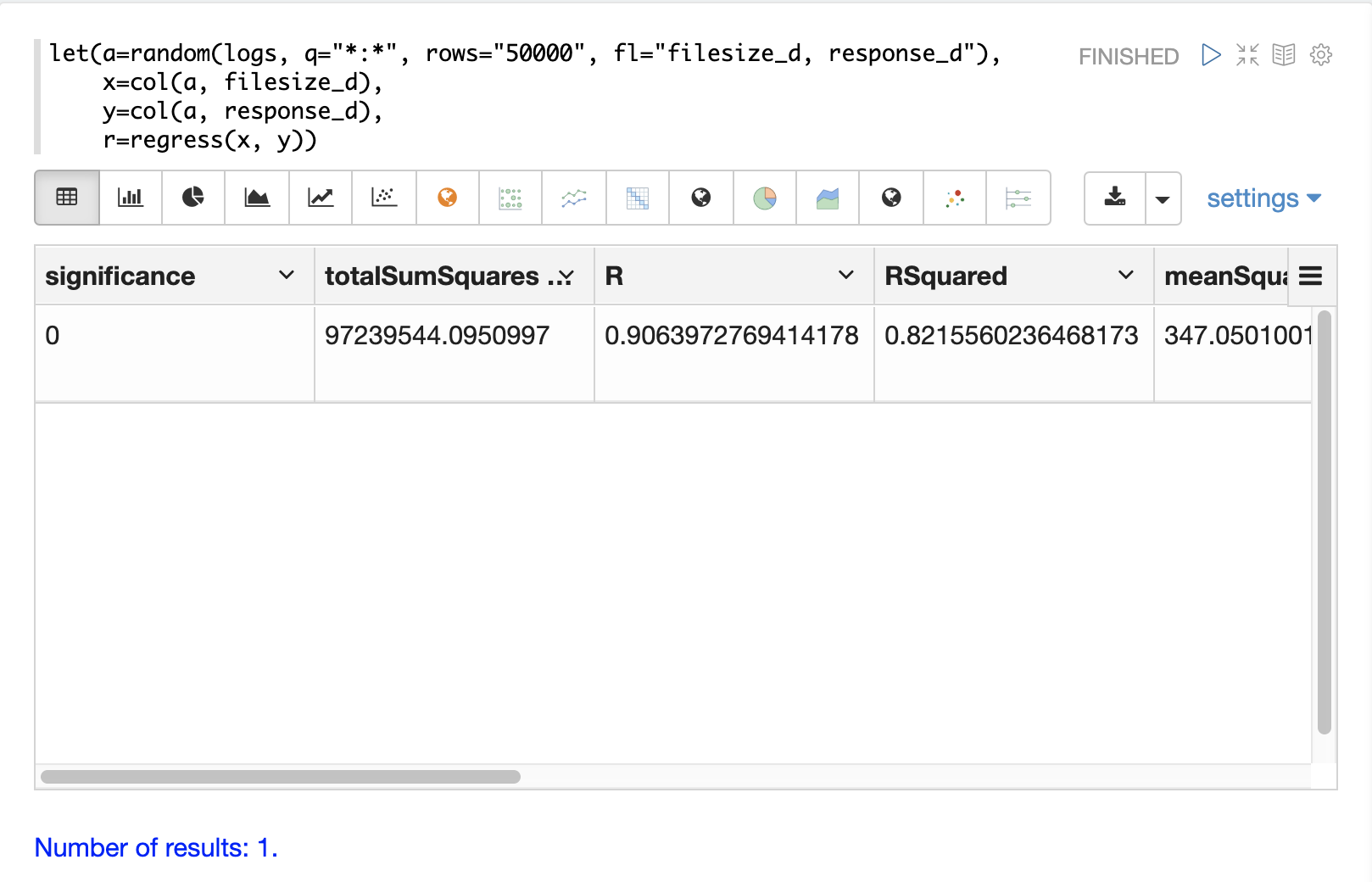
let(a=random(logs, q="*:*", rows="50000", fl="filesize_d, response_d"),
x=col(a, filesize_d),
y=col(a, response_d),
r=regress(x, y))この回帰分析では、RSquared の値が .75 であることに注意してください。これは、filesize_d の変化が response_d 変動の 75% を説明することを意味します。
{
"result-set": {
"docs": [
{
"significance": 0,
"totalSumSquares": 96595678.64838874,
"R": 0.9052835767815126,
"RSquared": 0.8195383543903288,
"meanSquareError": 348.6502485633668,
"intercept": 55.64040842391729,
"slopeConfidenceInterval": 0.0000822026526346821,
"regressionSumSquares": 79163863.52071753,
"slope": 0.019984612363694493,
"interceptStdErr": 1.6792610845256566,
"N": 50000
},
{
"EOF": true,
"RESPONSE_TIME": 344
}
]
}
}診断結果は、Zeppelin-Solr を使用して表で視覚化できます。
予測
predict 関数は、回帰モデルを使用して予測を行います。上記の例を使用すると、回帰モデルを使用して、filesize_d の値が与えられた場合に response_d の値を予測できます。
以下の例では、predict 関数は回帰分析を使用して、filesize_d の値が 40000 の場合の response_d の値を予測します。
let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
x=col(a, filesize_d),
y=col(a, response_d),
r=regress(x, y),
p=predict(r, 40000))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"p": 748.079241022975
},
{
"EOF": true,
"RESPONSE_TIME": 95
}
]
}
}predict 関数は、値の配列に対する予測も行うことができます。この場合、予測の配列が返されます。
以下の例では、predict 関数は回帰分析を使用して、モデルの生成に使用された filesize_d の 5000 サンプルそれぞれの値を予測します。この場合、5000 件の予測が返されます。
let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
x=col(a, filesize_d),
y=col(a, response_d),
r=regress(x, y),
p=predict(r, x))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"p": [
742.2525322514165,
709.6972488729955,
687.8382568904871,
820.2511324266264,
720.4006432289061,
761.1578181053039,
759.1304101159126,
699.5597256337142,
742.4738911248204,
769.0342605881644,
746.6740473150268
]
},
{
"EOF": true,
"RESPONSE_TIME": 113
}
]
}
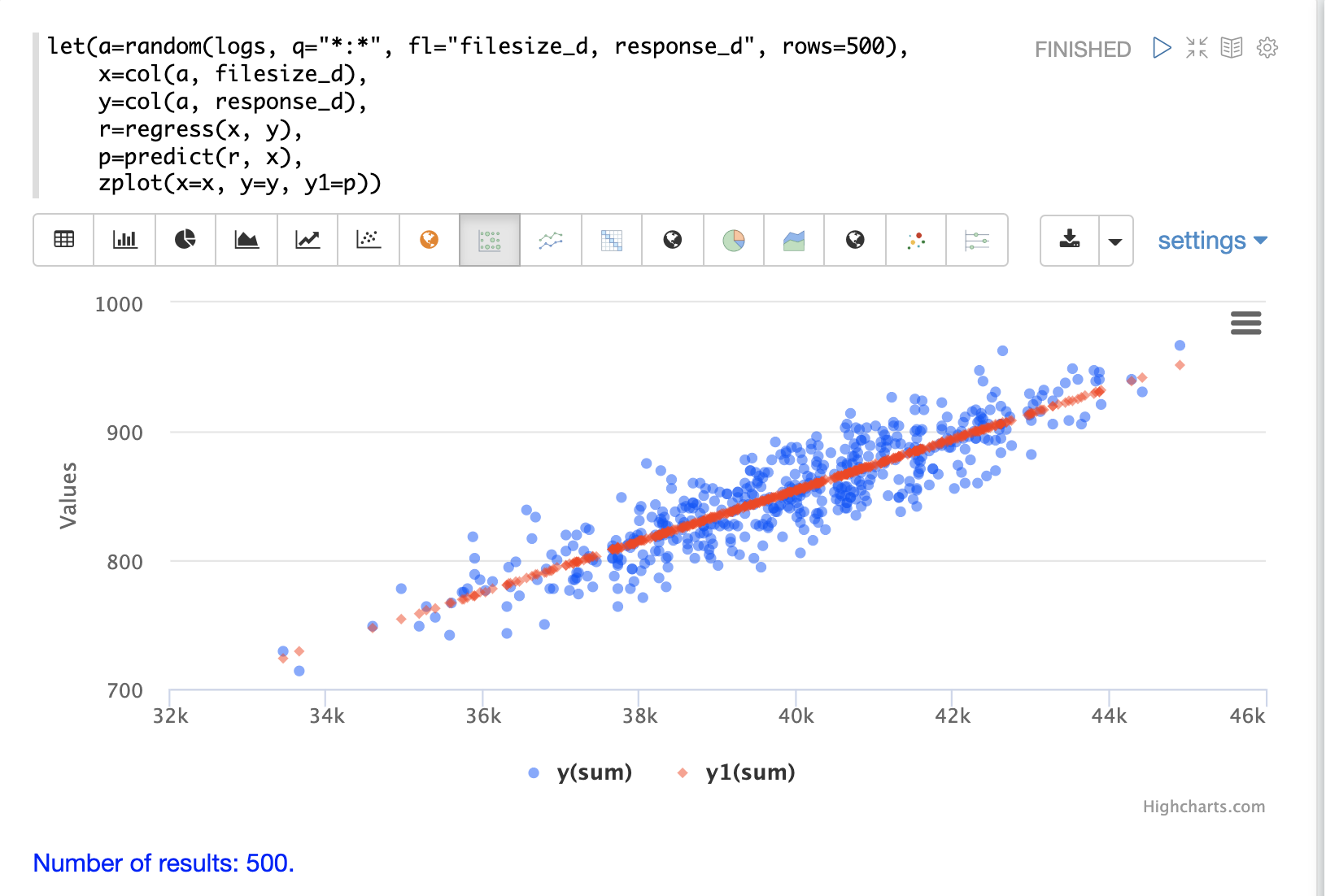
}回帰プロット
zplot と Zeppelin-Solr インタープリターを使用すると、観測値と予測値の両方を同じ散布図で視覚化できます。以下の例では、zplot が x 軸に filesize_d の観測値、y 軸に response_d の観測値、y1 軸に予測値をプロットしています。
残差
観測値と予測値の差は、残差として知られています。残差を計算するための特定の関数はありませんが、ベクトル演算を使用して計算を実行できます。
以下の例では、予測値は変数 p に格納されます。次に、ebeSubtract 関数を使用して、変数 y に格納されている実際の response_d の値から予測値を減算します。変数 e には、残差の配列が含まれます。
let(a=random(logs, q="*:*", rows="500", fl="filesize_d, response_d"),
x=col(a, filesize_d),
y=col(a, response_d),
r=regress(x, y),
p=predict(r, x),
e=ebeSubtract(y, p))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"e": [
31.30678554491226,
-30.292830927953446,
-30.49508862647258,
-30.499884780783532,
-9.696458959319784,
-30.521563961535094,
-30.28380938033081,
-9.890289849359306,
30.819723560583157,
-30.213178859683012,
-30.609943619066826,
10.527700442607625,
10.68046928406568
]
},
{
"EOF": true,
"RESPONSE_TIME": 113
}
]
}
}残差プロット
zplot と Zeppelin-Solr を使用して、残差を残差プロットで視覚化できます。以下の残差プロットの例では、x 軸に予測値、y 軸に予測の誤差をプロットしています。
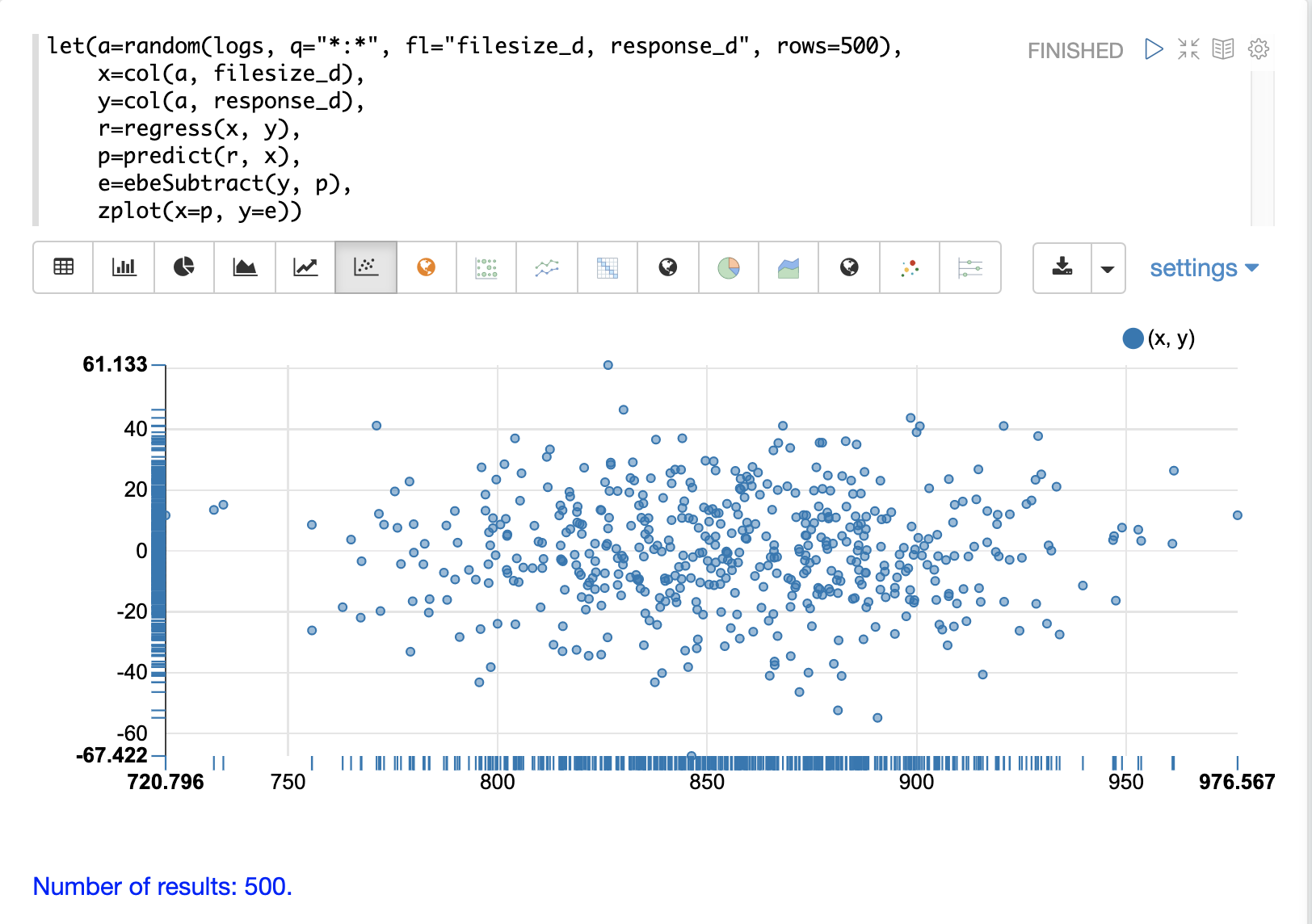
残差プロットを使用して、モデルの信頼性を解釈できます。注目すべき3つの点は次のとおりです。
-
残差は平均 0 で正規分布しているように見えますか?これにより、モデルの結果を解釈して、予測に対する誤差の分布が許容できるかどうかを判断することが容易になります。また、新しい予測に関する異常検出のために、残差のモデルを使用することも容易になります。
-
残差は異分散性に見えますか?つまり、残差の分散は、予測の範囲全体で同じですか?x 軸に予測を、y 軸に誤差をプロットすることにより、予測が高くなるにつれて変動が同じままかどうかを確認できます。残差が異分散性である場合、モデルの誤差が予測の範囲全体で一貫していると信頼できることを意味します。
-
残差に何らかのパターンはありますか?もしあれば、モデル化する必要のあるデータ内にまだ信号がある可能性があります。
多変量線形回帰
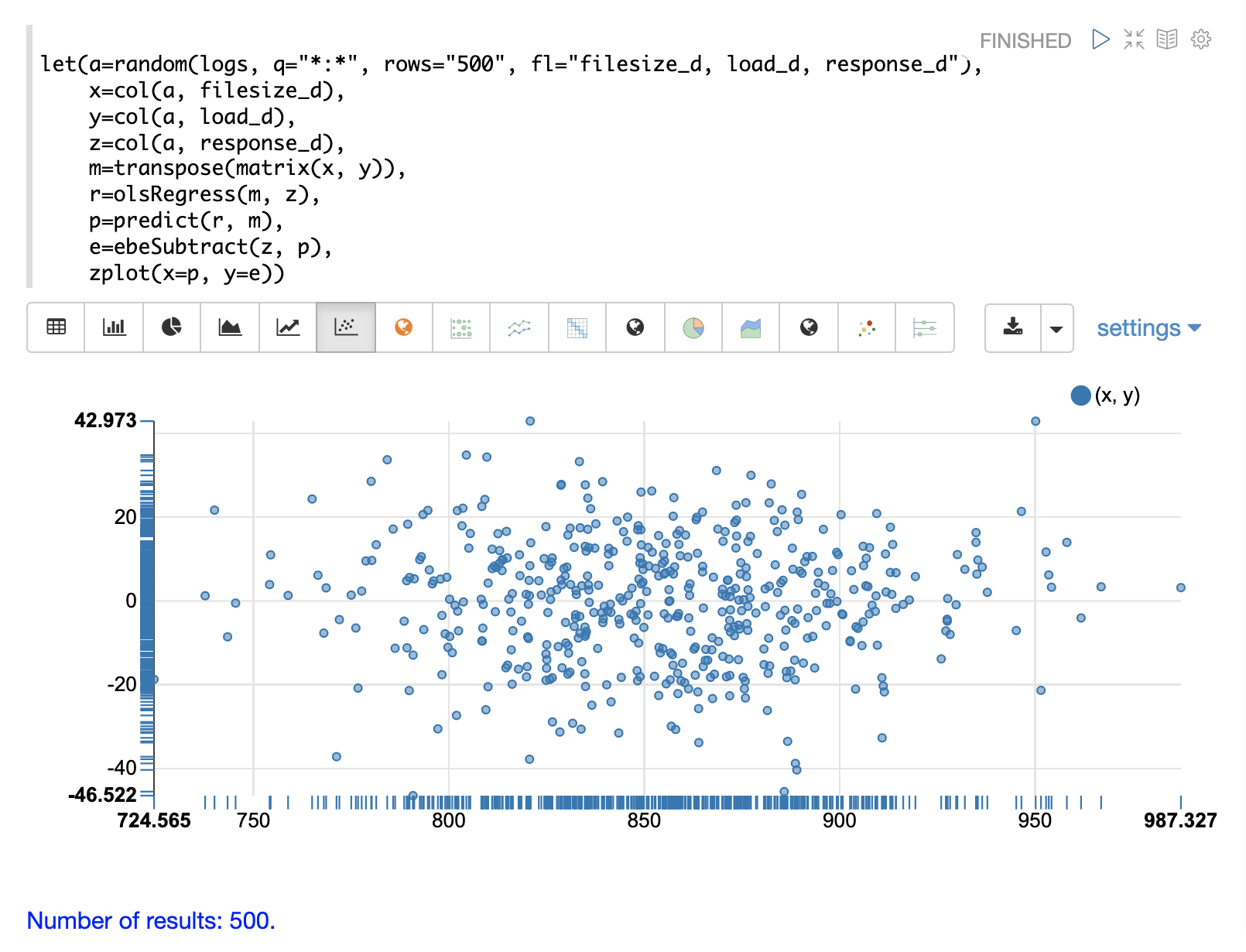
olsRegress 関数は、多変量線形回帰分析を実行します。多変量線形回帰は、2つ以上の独立変数と従属変数間の線形関係をモデル化します。
以下の例は、単純線形回帰の例を拡張し、load_d という新しい独立変数を導入しています。load_d 変数は、ファイルのダウンロード中のネットワーク負荷を表します。
2つの独立変数 filesize_d と load_d はベクトル化され、変数 b と c に格納されていることに注意してください。次に、変数 b と c は matrix に行として追加されます。次に、行列は転置され、行列の各行が filesize_d と service_d を持つ1つの観測値を表すようになります。次に、olsRegress 関数は、観測値行列を独立変数として、変数 d に格納された response_d 値を従属変数として使用して、多変量回帰分析を実行します。
let(a=random(testapp, q="*:*", rows="30000", fl="filesize_d, load_d, response_d"),
x=col(a, filesize_d),
y=col(a, load_d),
z=col(a, response_d),
m=transpose(matrix(x, y)),
r=olsRegress(m, z))レスポンスでは、回帰分析の RSquared が 1 であることに注意してください。これは、filesize_d と service_d の間の線形関係が、response_d 変数の変動の100%を説明することを意味します。
{
"result-set": {
"docs": [
{
"regressionParametersStandardErrors": [
1.7792032752524236,
0.0000429945089590394,
0.0008592489428291642
],
"RSquared": 0.8850359458670845,
"regressionParameters": [
0.7318766882597804,
0.01998298784650873,
0.10982104952105468
],
"regressandVariance": 1938.8190758686717,
"regressionParametersVariance": [
[
0.014201127587649602,
-3.326633951803927e-7,
-0.000001732754417954437
],
[
-3.326633951803927e-7,
8.292732891338694e-12,
2.0407522508189773e-12
],
[
-0.000001732754417954437,
2.0407522508189773e-12,
3.3121477630934995e-9
]
],
"adjustedRSquared": 0.8850282808303053,
"residualSumSquares": 6686612.141261716
},
{
"EOF": true,
"RESPONSE_TIME": 374
}
]
}
}予測
predict 関数は、多変量線形回帰の予測を行うためにも使用できます。
以下は、多変量線形回帰モデルと単一の観測値を使用して単一の予測を行う例です。観測値は、モデルの構築に使用された観測値行列の構造と一致する配列です。この場合、最初の値は 40000 の filesize_d を表し、2番目の値は 4 の load_d を表します。
let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
x=col(a, filesize_d),
y=col(a, load_d),
z=col(a, response_d),
m=transpose(matrix(x, y)),
r=olsRegress(m, z),
p=predict(r, array(40000, 4)))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"p": 801.7725344814675
},
{
"EOF": true,
"RESPONSE_TIME": 70
}
]
}
}predict 関数は、複数の多変量観測値の予測も行うことができます。このシナリオでは、観測値行列が使用されます。
以下の例では、多変量回帰モデルの構築に使用された観測値行列が predict 関数に渡され、予測の配列が返されます。
let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
x=col(a, filesize_d),
y=col(a, load_d),
z=col(a, response_d),
m=transpose(matrix(x, y)),
r=olsRegress(m, z),
p=predict(r, m))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"p": [
917.7122088913725,
900.5418518783401,
871.7805676516689,
822.1887964840801,
828.0842807117554,
785.1262470470162,
833.2583851225845,
802.016811579941,
841.5253327135974,
896.9648275225625,
858.6511235977382,
869.8381475112501
]
},
{
"EOF": true,
"RESPONSE_TIME": 113
}
]
}
}残差
予測が生成されたら、単純線形回帰で使用したのと同じ方法を使用して残差を計算できます。
以下は、多変量線形回帰後の残差計算の例です。例では、変数 g に格納された予測値が、変数 d に格納された観測値から減算されています。
let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, load_d, response_d"),
x=col(a, filesize_d),
y=col(a, load_d),
z=col(a, response_d),
m=transpose(matrix(x, y)),
r=olsRegress(m, z),
p=predict(r, m),
e=ebeSubtract(z, p))この式が /stream ハンドラに送信されると、次のように応答します。
{
"result-set": {
"docs": [
{
"e": [
21.452271655340496,
9.647947283595727,
-23.02328008866334,
-13.533046479596806,
-16.1531952414299,
4.966514036315402,
23.70151322413119,
-4.276176642246014,
10.781062392156628,
0.00039750380267378205,
-1.8307638852961645
]
},
{
"EOF": true,
"RESPONSE_TIME": 113
}
]
}
}