曲線フィッティング
これらの関数は、二変数の非線形データを通る曲線を構築することをサポートします。
多項式曲線フィッティング
polyfit 関数は、2つのランダム変数間の非線形関係をモデル化するために使用される汎用曲線フィッターです。
polyfit 関数は、x軸とy軸を渡され、データに滑らかな曲線をフィッティングします。単一の配列のみが提供された場合、それはy軸として扱われ、x軸のシーケンスが生成されます。多項式の次数を指定する3番目のパラメータを追加できます。次数が提供されない場合、デフォルトで3次多項式が使用されます。次数が高いほど、モデル化できる曲線が増えます。
polyfit 関数は、Zeppelin-Solrを使用した線形回帰と同様の方法で視覚化できます。
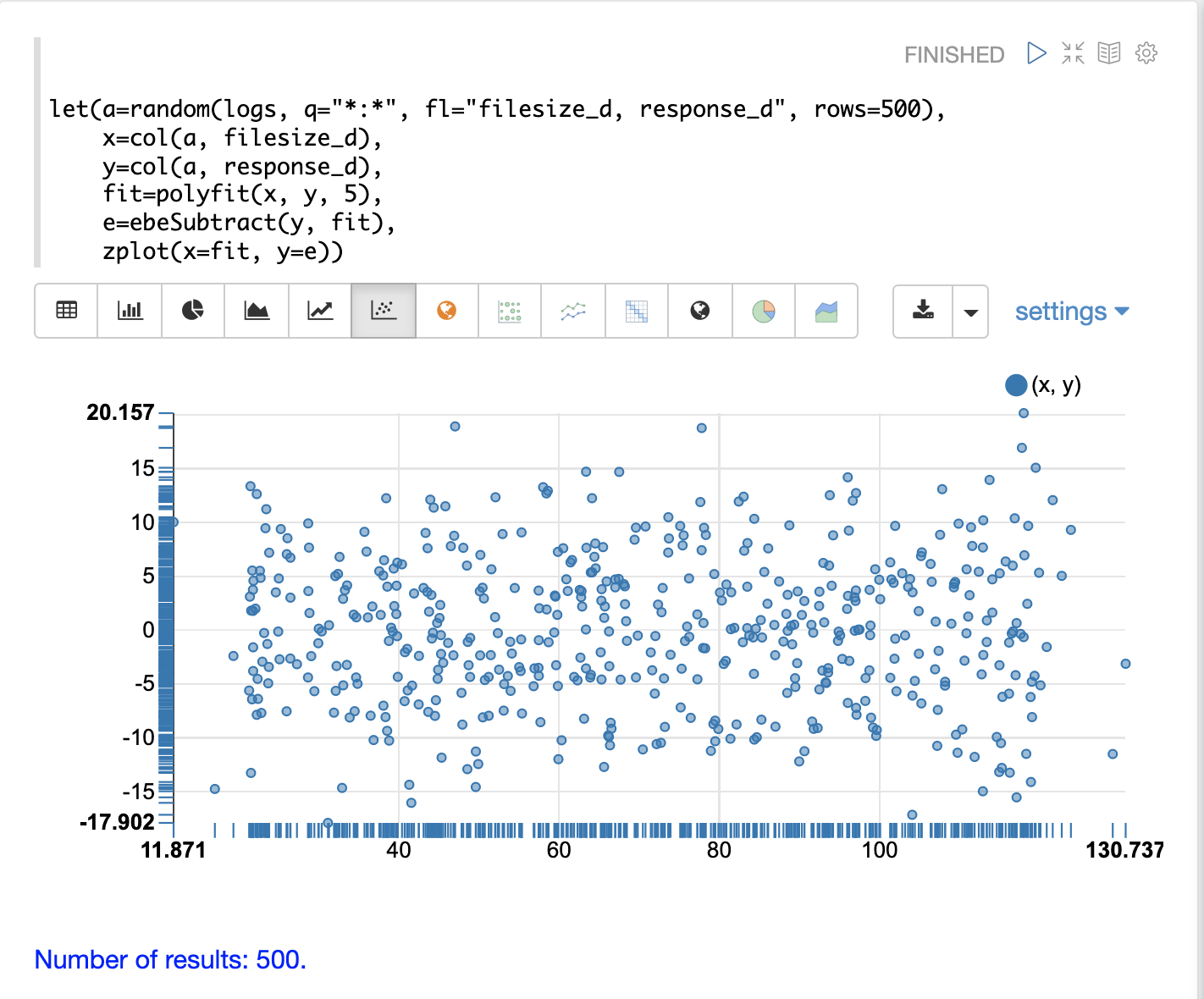
以下の例では、polyfit 関数を使用して、ランダムサンプルの散布図に非線形曲線をフィッティングします。青い点は元の観測値の散布図であり、赤い点は予測された曲線です。
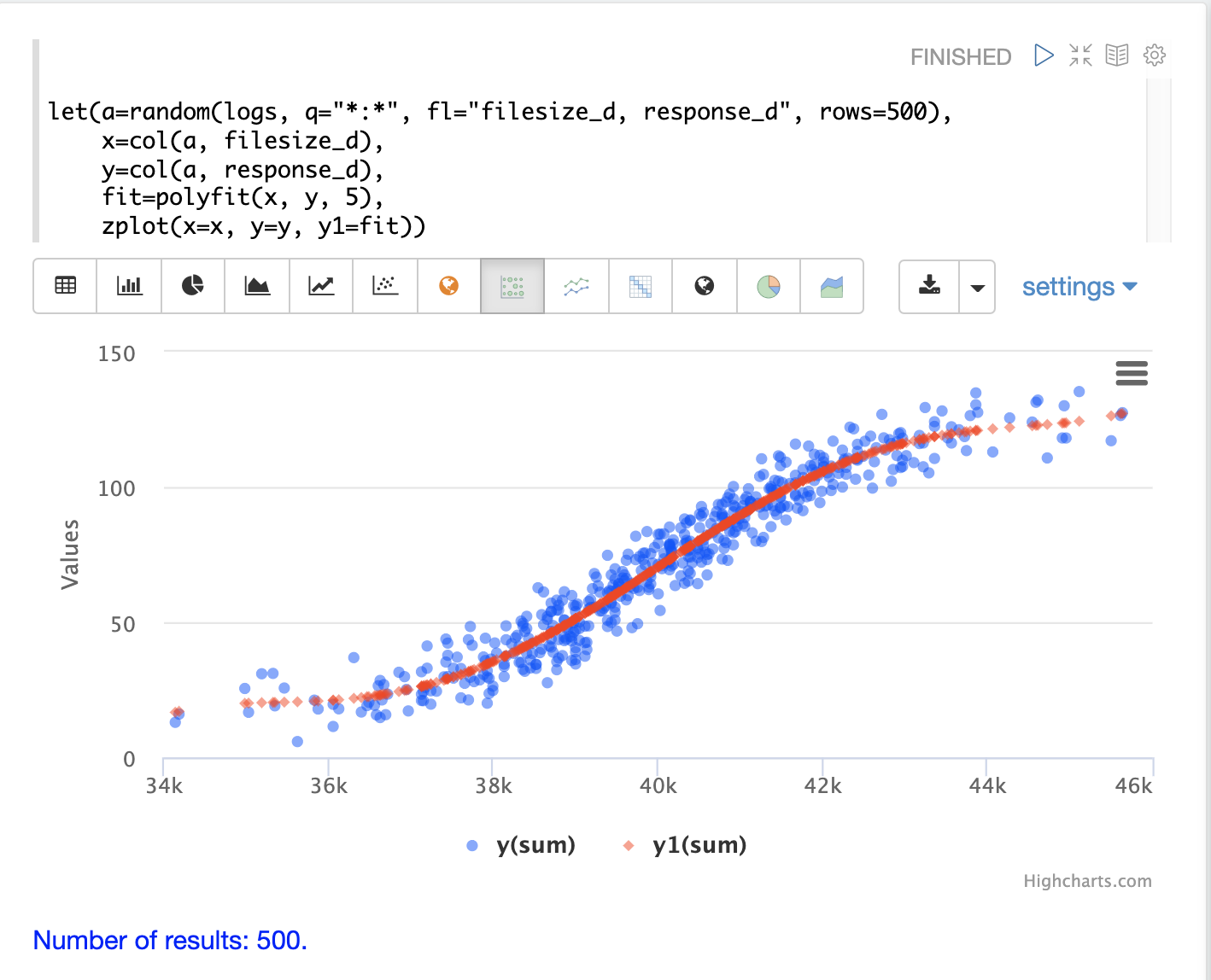
上記の例では、filesize_d と response_d の2つのフィールドを含むランダムサンプルが、logs コレクションから抽出されます。2つのフィールドはベクトル化され、変数 x と y に設定されます。
次に、polyfit 関数を使用して、5次多項式を使用してデータに非線形モデルをフィッティングします。polyfit 関数は、元の観測値とともに zplot によって直接プロットされるモデルを返します。
フィッティングされたモデルは、線形回帰と同じように predict 関数でも使用できます。以下の例では、フィッティングされたモデルを使用して、ファイルサイズが 42000 の場合の応答時間を予測しています。
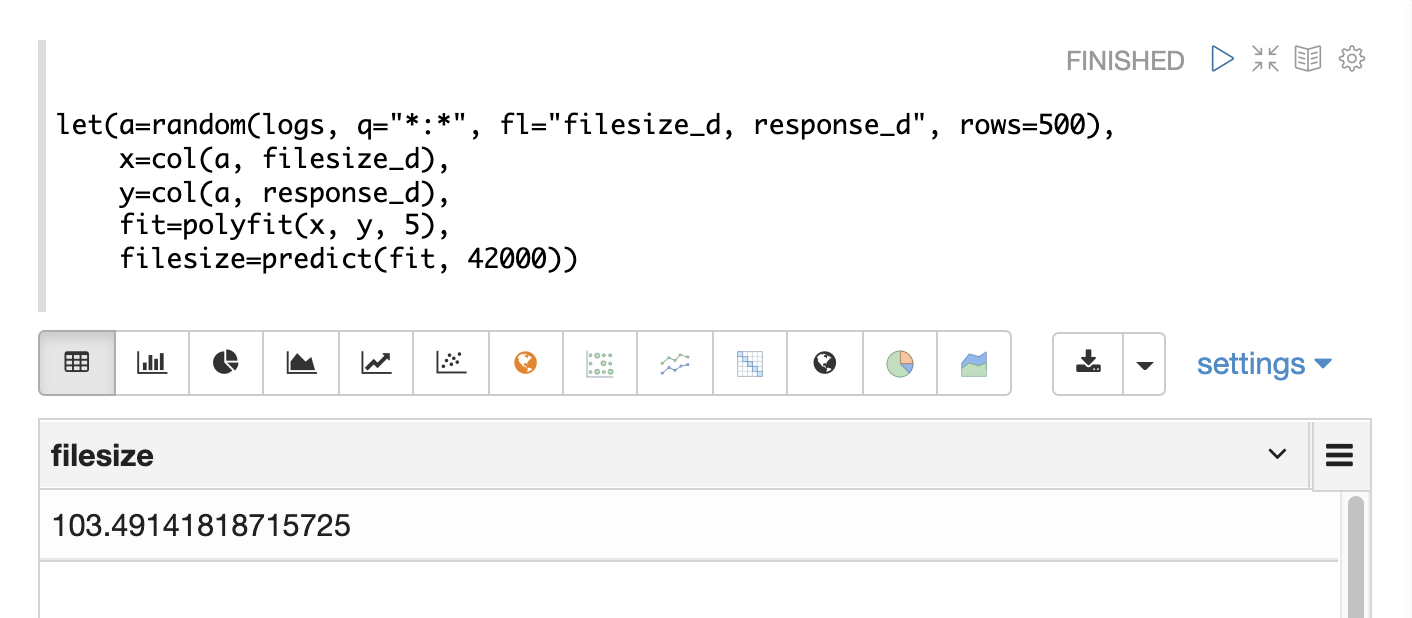
予測値の配列が提供された場合、予測の配列が返されます。
polyfit モデルは、**補間**と**外挿**の両方を行うため、データセットの境界内と境界外の両方で結果を予測できます。
ガウス曲線フィッティング
gaussfit 関数は、ガウスピークを通る滑らかな曲線をフィッティングします。gaussfit 関数は、x軸とy軸を受け取り、データに滑らかなガウス曲線をフィッティングします。数値のベクトルが1つだけ渡された場合、gaussfit はそれをy軸として扱い、x軸のシーケンスを生成します。
gaussfit の興味深いユースケースの1つは、回帰モデルの残差が正規分布にどれだけ適合するかを視覚化することです。
適切に適合した回帰モデルの特性の1つは、その残差が理想的には正規分布に適合することです。これをテストするには、残差のヒストグラムを作成し、ヒストグラムの曲線にガウス曲線をフィッティングします。
以下の例では、polyfit 回帰からの残差が、32個のビンを持つヒストグラムを返す hist 関数でモデル化されています。hist 関数は、各ビンに関する統計情報を持つタプルのリストを返します。例では、col 関数を使用して、各ビンの N 列を持つベクトルを返します。これは、ビン内の観測数です。残差が正規分布している場合、ビンのカウントはほぼガウス曲線に従うと予想されます。
次に、ビンのカウントベクトルがy軸として gaussfit に渡されます。gaussfit は、x軸のシーケンスを生成し、その後、データにガウス曲線をフィッティングします。
次に、zplot を使用して、元のビンのカウントとフィッティングされた曲線をプロットします。以下の例では、青い線がビンのカウントで、滑らかな黄色の線がフィッティングされた曲線です。ビン分割された残差が正規分布にかなりよく適合していることがわかります。
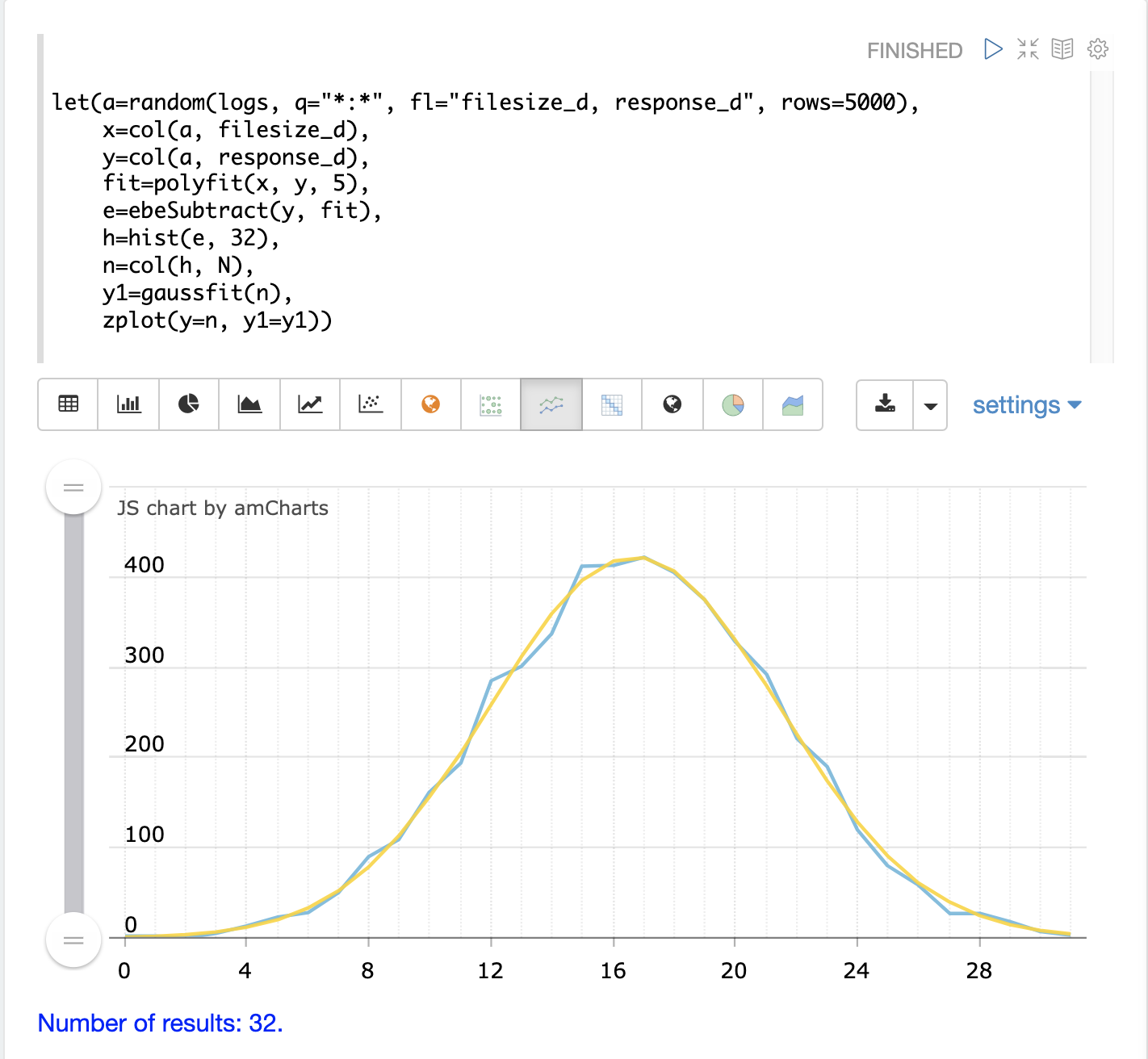
2番目のプロットは、2つの曲線を面グラフで重ねて表示しています。
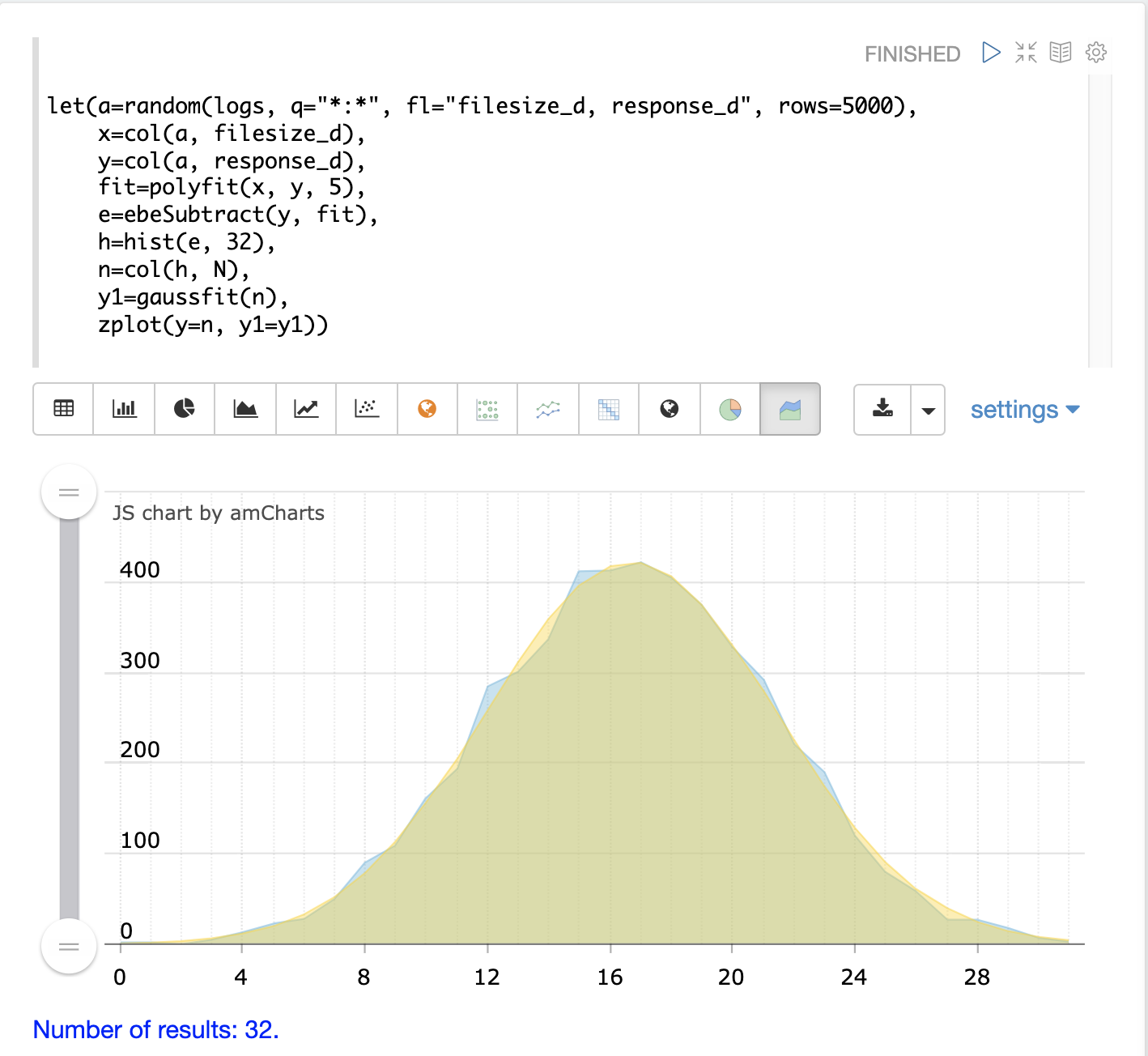
調和曲線フィッティング
harmonicFit 関数 (または略して harmfit) は、正弦波の制御点を通過する滑らかな線をフィッティングします。harmfit 関数には、x軸とy軸が渡され、データに滑らかな曲線をフィッティングします。単一の配列が提供された場合、それはy軸として扱われ、x軸のシーケンスが生成されます。
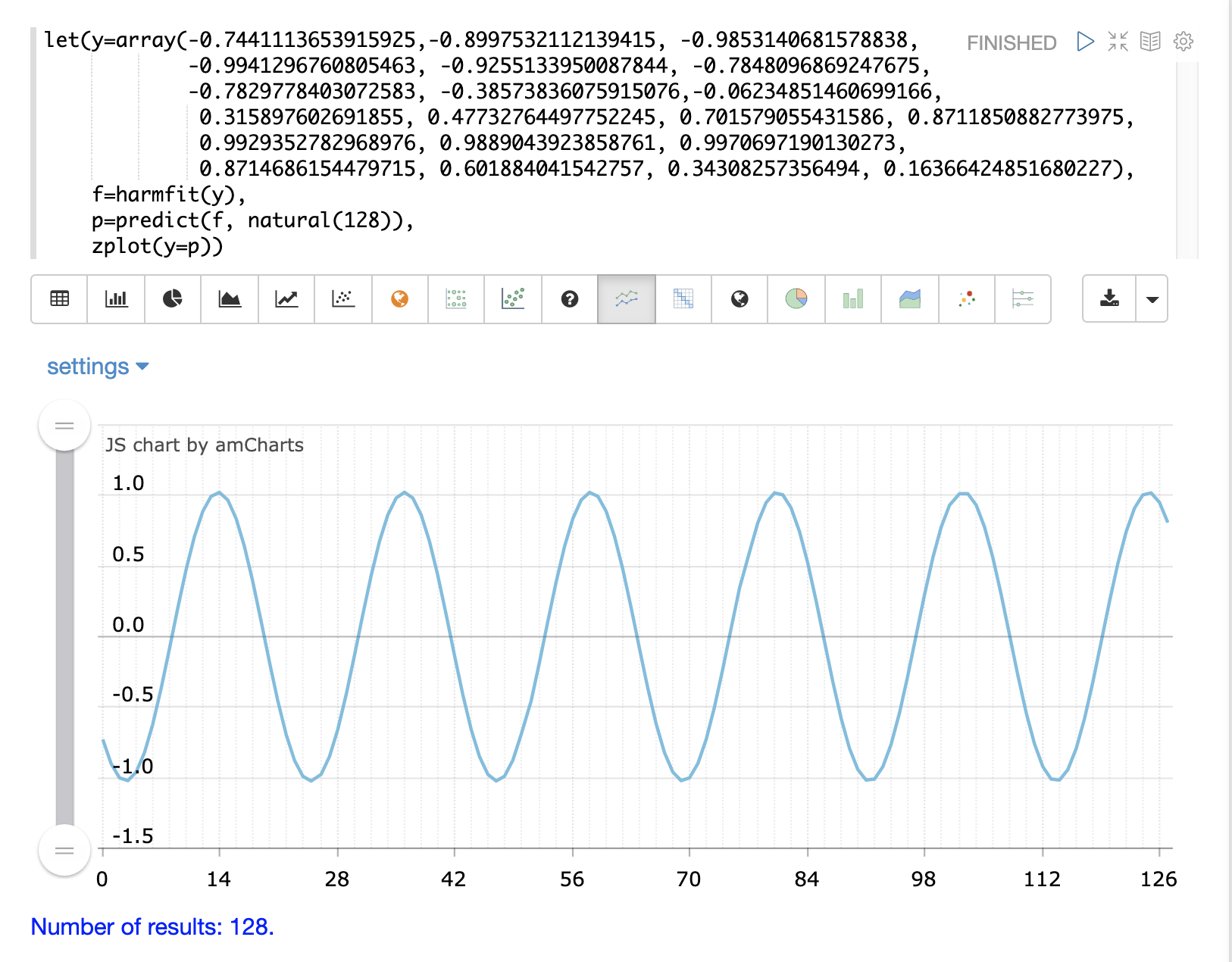
以下の例は、正弦波の単一の振動に harmfit がフィッティングしている様子を示しています。harmfit 関数は、各制御点での平滑化された値を返します。戻り値はモデルでもあり、predict、derivative、および integrate 関数で使用できます。
harmfit 関数は、長い振動シーケンスではなく、単一の振動で実行すると最適に機能します。これは特に、正弦波にノイズがある場合に当てはまります。曲線がフィッティングされた後、過去または未来の任意の時点に外挿できます。 |
以下の例では、元の制御点が青色で表示され、フィッティングされた曲線が黄色で表示されています。
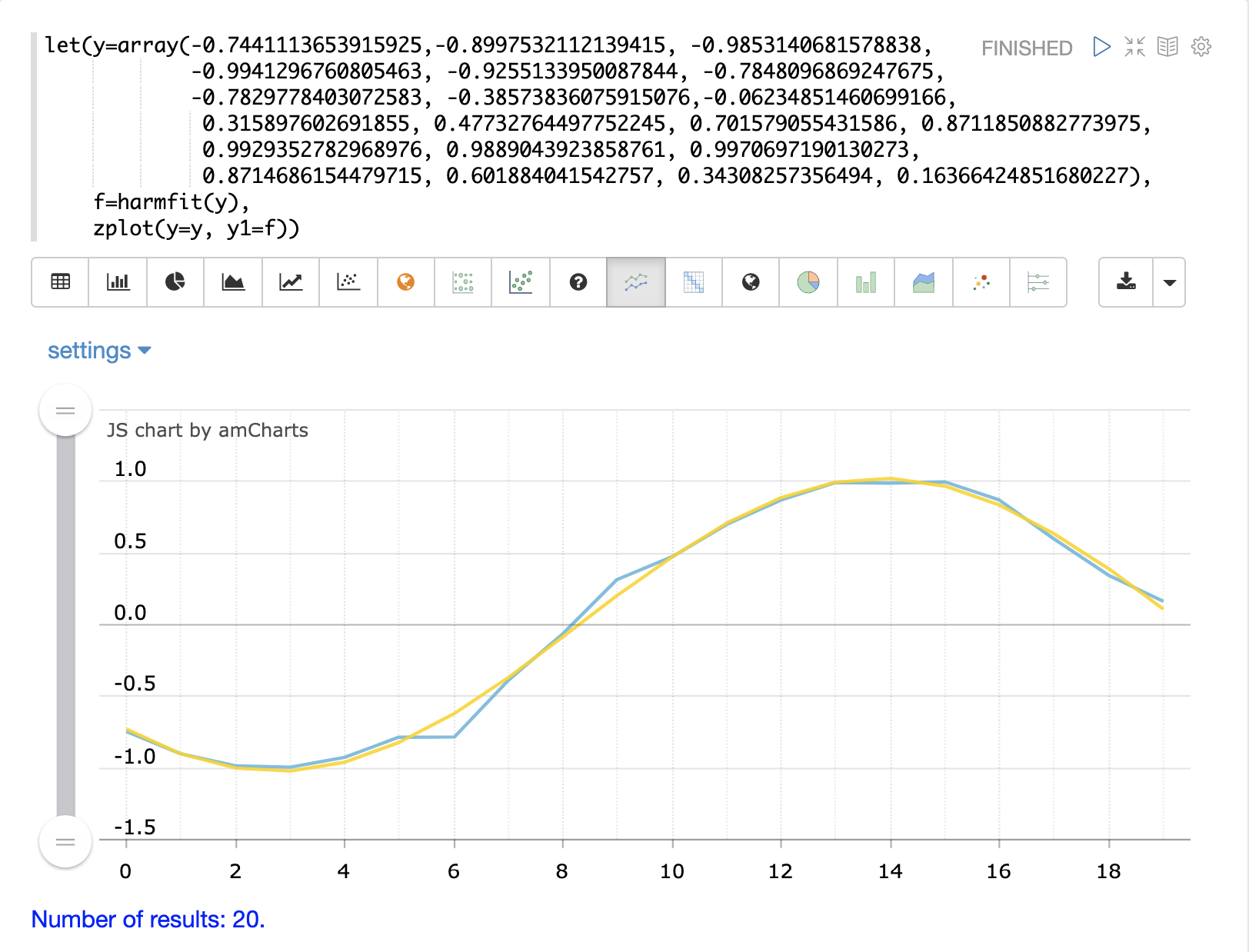
harmfit の出力は、predict 関数で使用して、正弦波を補間および外挿できるモデルです。以下の例では、natural 関数は、モデルの結果を予測するために使用される0から127までのx軸を作成します。これにより、元のモデル曲線が19個の制御点しか持っていなかった場合に、正弦波が128点まで外挿されます。