デジタル信号処理
このセクションでは、デジタル信号処理(DSP)の分野で一般的に使用される関数を解説します。
畳み込み
conv関数は、2つのベクトルの畳み込みを計算します。畳み込みは、2番目のベクトルを反転させ、それを最初のベクトルに沿ってスライドさせることで計算されます。2番目のベクトルが最初のベクトルに沿ってスライドする各点で、2つのベクトルのドット積が計算されます。ドット積は、2つのベクトルの畳み込みである3番目のベクトルに収集されます。
移動平均関数
畳み込みの例を見る前に、movingAvg関数を検討することが役立ちます。移動平均関数は、ウィンドウをベクトルに沿ってスライドさせ、各シフトでウィンドウの平均を計算することにより、移動平均を計算します。それが畳み込みに似ているように聞こえるなら、それはmovingAvg関数が畳み込みと同様のスライディングウィンドウアプローチを含むためです。
以下は、ウィンドウサイズ5の移動平均の例です。元のベクトルには13個の要素がありますが、移動平均の結果には9個の要素しかありません。これは、movingAvg関数が完全なウィンドウが揃ってから結果の生成を開始するためです。ltrim関数は、移動平均と一致するように元のy配列から最初の4つの要素を切り捨てるために使用されます。
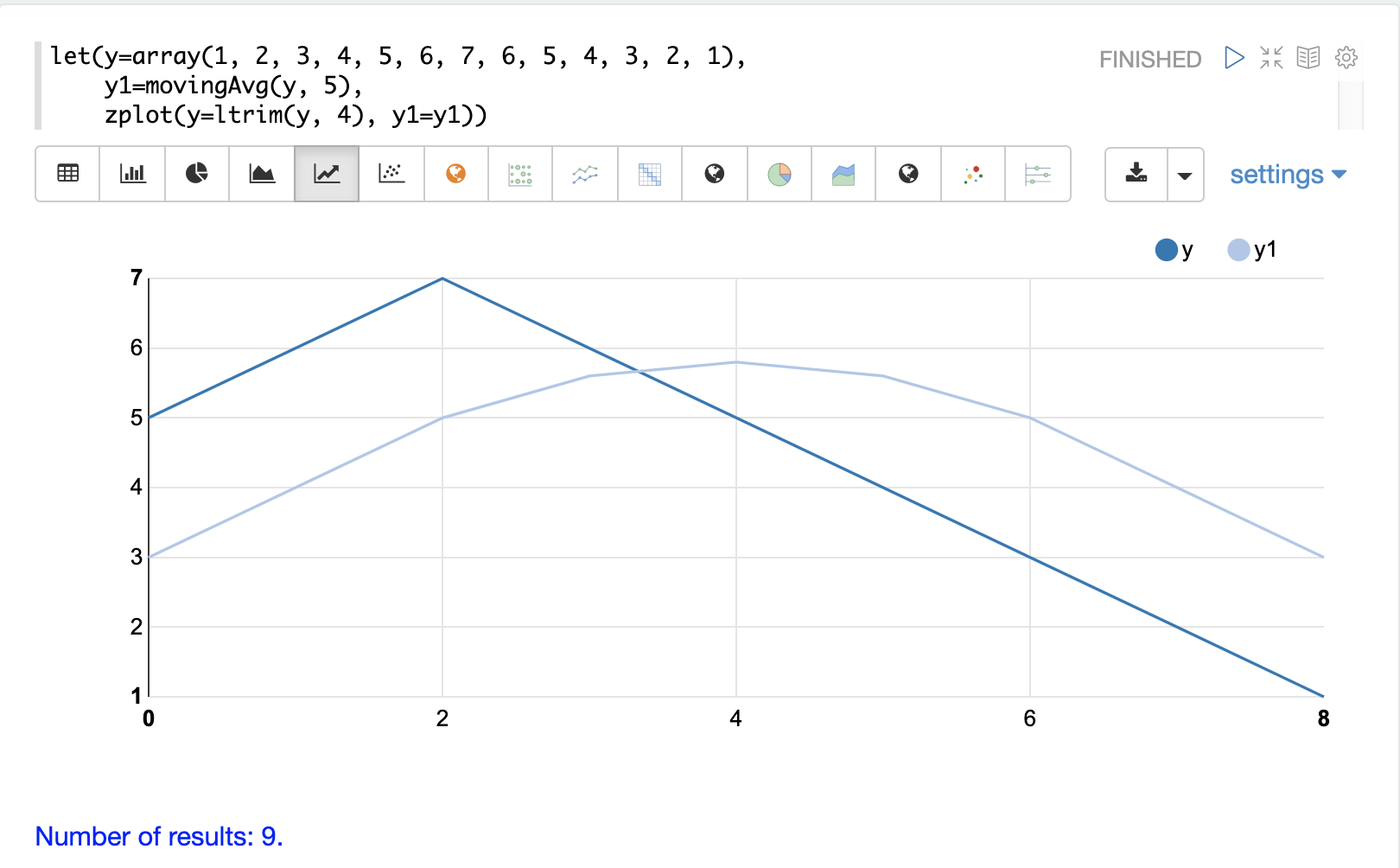
畳み込みによる平滑化
移動平均は、畳み込みを使用して計算することもできます。以下の例では、conv関数は、2番目の配列をフィルタとして適用することにより、最初の配列の移動平均を計算するために使用されます。
結果を見ると、畳み込みは9個の値を持つ移動平均ではなく、17個の値を持つ配列を生成していることがわかります。これは、conv関数がウィンドウサイズが常に満たされるように、最初のベクトルの前後にゼロを埋め込むためです。
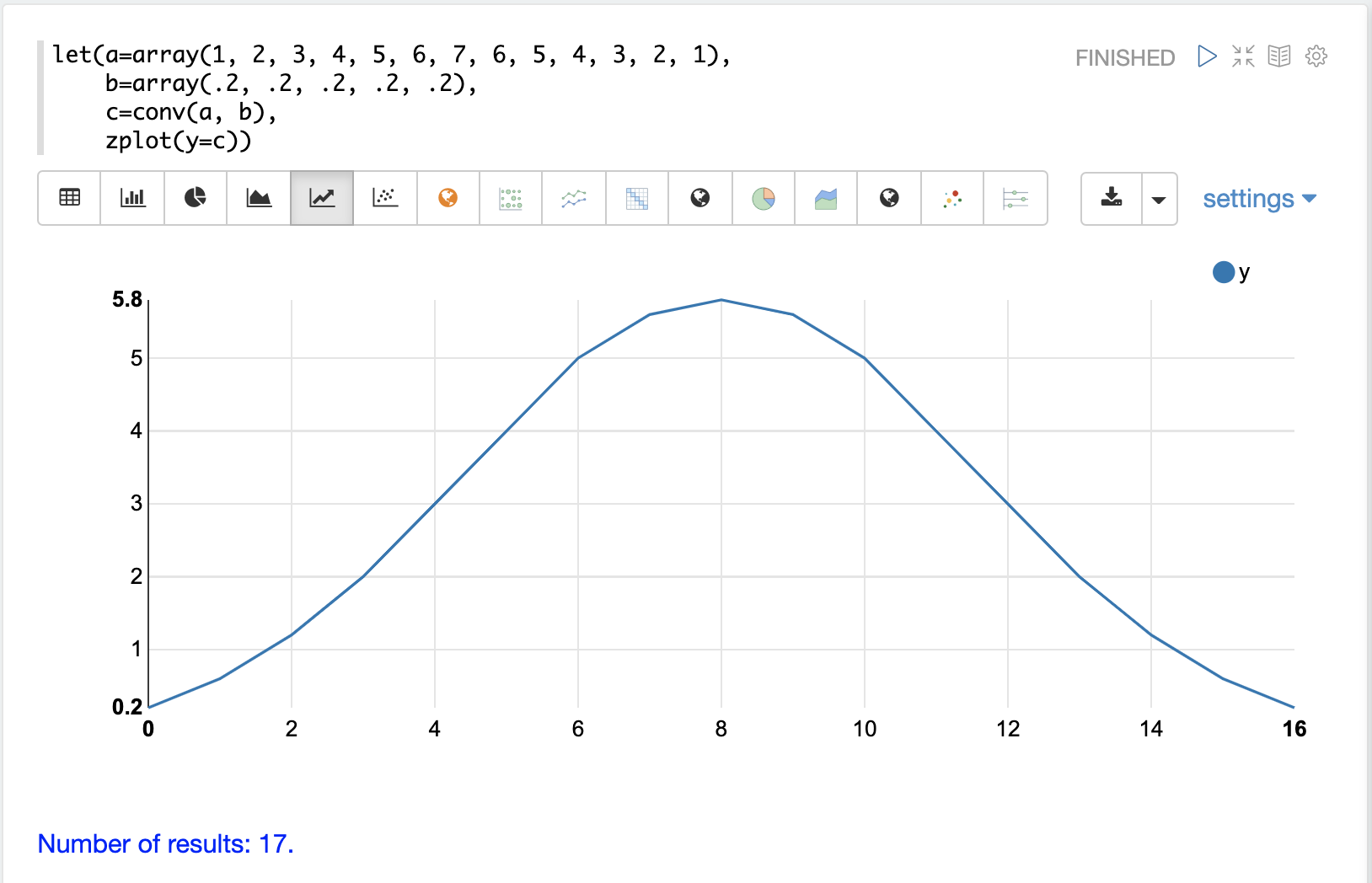
ltrim関数とrtrim関数を使用して、畳み込み結果の先頭と末尾の4つの値を切り捨てることで、movingAvg関数と同じ結果を得ることができます。
以下の例では、切り詰められた畳み込みと移動平均の両方を同じプロットにプロットしています。完全に重なっていることに注意してください。
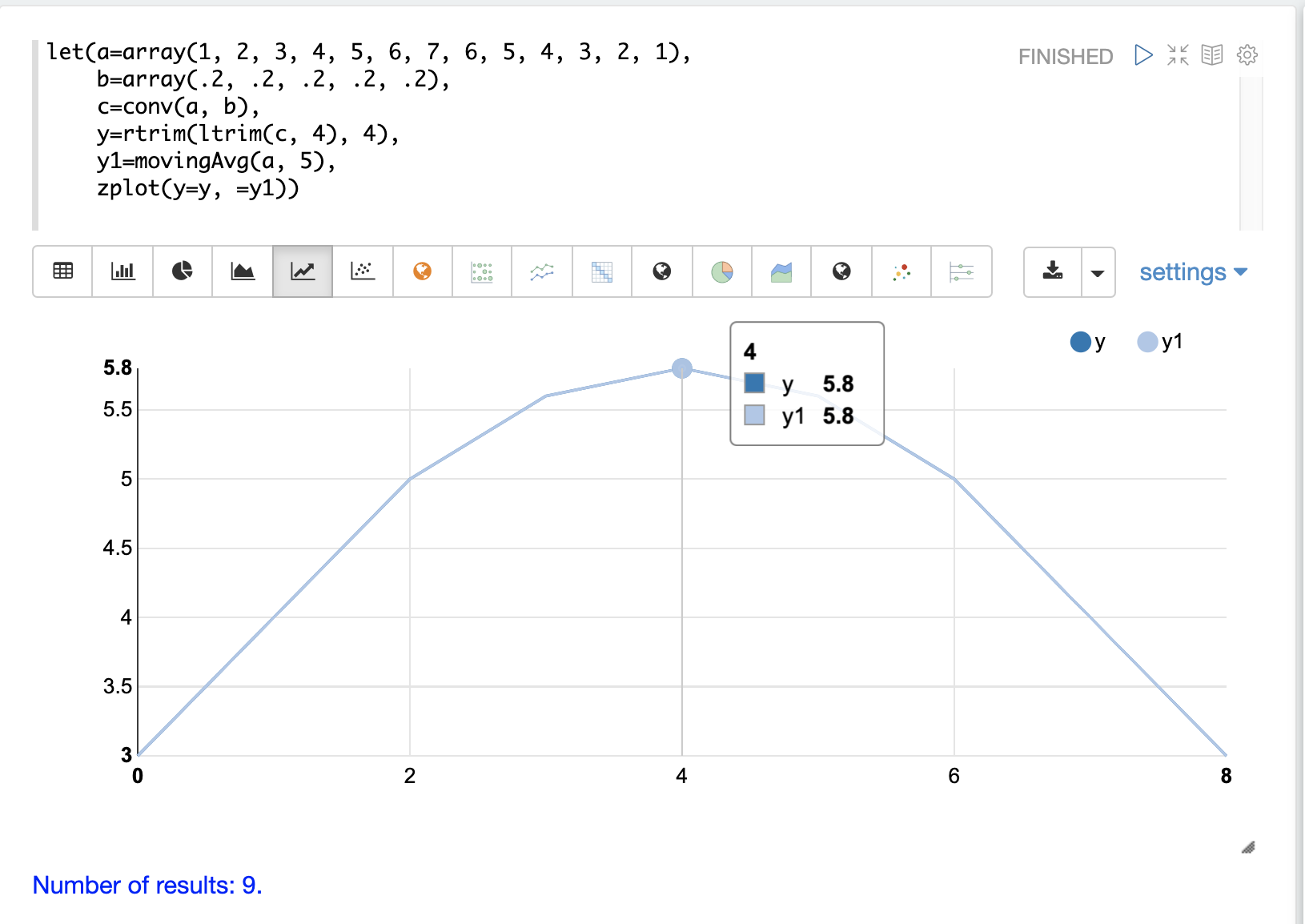
これは、畳み込みを使用して、フィルタを信号に沿ってスライドさせ、各点でドット積を計算することにより信号を平滑化できることを示しています。平滑化効果は、フィルタの設計によって引き起こされます。この例では、フィルタの長さは5で、フィルタ内の各値は0.2です。このフィルタは、ウィンドウサイズ5の単純移動平均を計算します。
畳み込みを使用して単純移動平均を計算するための式は、フィルタの長さをウィンドウサイズにし、フィルタの値をすべて同じにし、合計を1にすることです。ウィンドウサイズ4の移動平均は、フィルタを長さ4に変更し、各値を0.25にすることで計算できます。
重みの変更
フィルタは、カーネルと呼ばれることもあります。フィルタは重みのベクトルと見なすことができます。最初の例では、フィルタ内のすべての値は同じ重み(0.2)を持っています。フィルタ内の重みを変更して、異なる平滑化効果を得ることができます。これは以下の例で示されています。
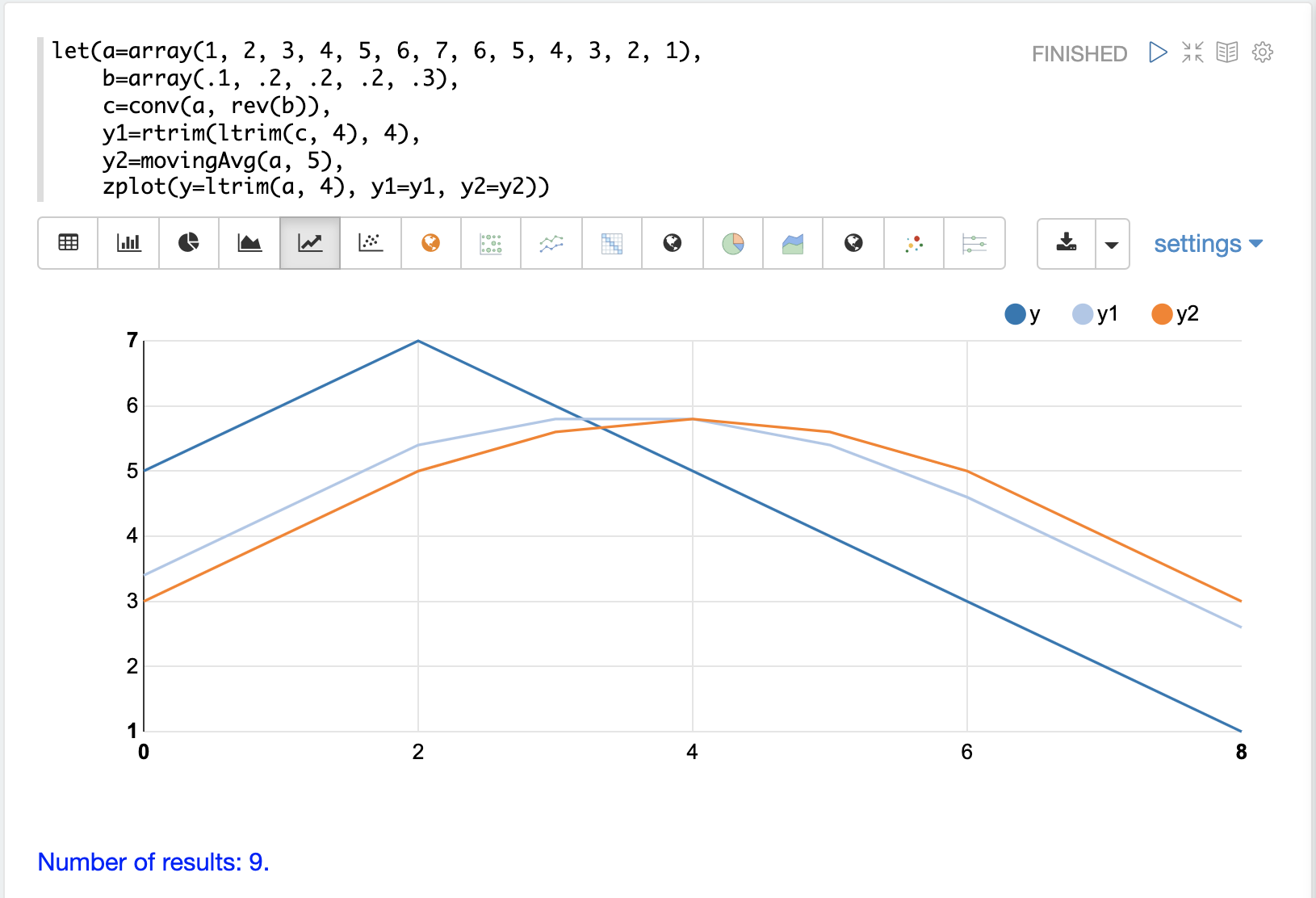
この例では、フィルタの重みが0.1から0.3に増加します。これにより、フィルタの先頭に大きな重みが置かれます。conv関数が適用される前に、rev関数を使用してフィルタが反転されることに注意してください。これは、畳み込みがフィルタを反転させるために行われます。この場合、事前に反転させ、畳み込みがそれを元に戻すと、元のフィルタと同じになります。
このプロットは、フィルタ内の異なる重みの効果を示しています。濃い青色の線は元の配列です。水色の線は畳み込みの結果、オレンジ色の線は移動平均の結果です。畳み込みは、基礎となる配列の動きに迅速に反応することに注目してください。これは、フィルタの先頭に多くの重みが置かれているためです。
相互相関
相互相関は、2つの信号間の遅延を決定するために使用されます。これは、一方の信号をもう一方の信号に沿ってスライドさせ、各シフトでドット積を計算することによって実現されます。ドット積はベクトルに収集され、各シフトでの相関を表します。相互相関ベクトルにおける最大のドット積は、2つの信号が最も密接に相関している点です。
畳み込みで使用されるスライド式ドット積は、2つのベクトル間の相互相関を表すためにも使用できます。相関を表す場合の式における唯一の違いは、第2のベクトルが**反転されていない**ことです。
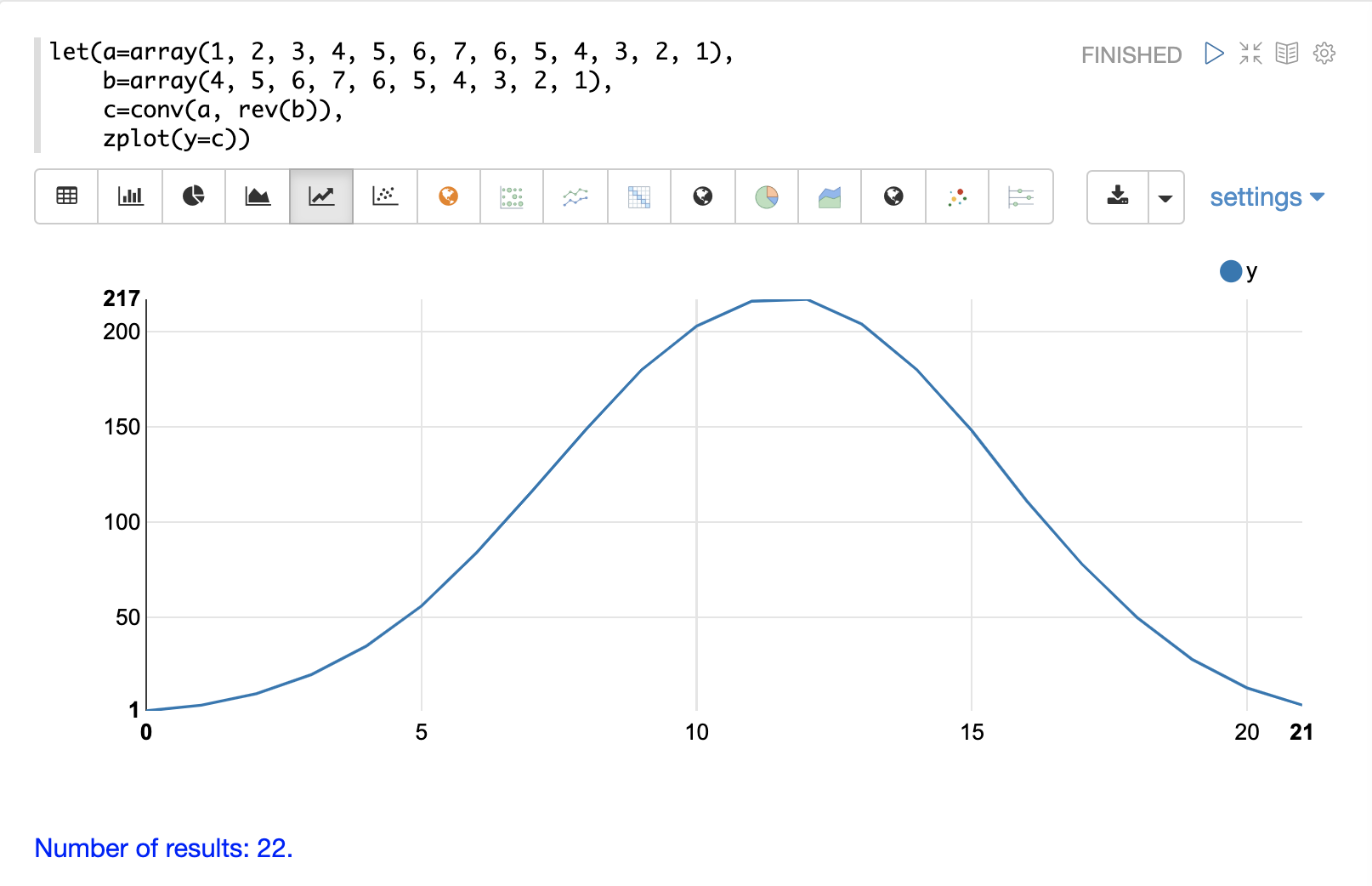
以下の例では、第2のベクトルがrev関数によって反転された後、conv関数によって演算されることに注目してください。conv関数は第2のベクトルを反転させるため、畳み込み計算ではなく相関計算を実行するために元の順序に戻されます。
結果で最も高い値が217であることに注目してください。これは、2つのベクトルが最も高い相関を持つ点です。
遅延の検出
相互相関の結果から遅延を計算することは非常に簡単ですが、finddelayと呼ばれる便利な関数を用いて遅延を直接求めることができます。内部的には、finddelayは畳み込みの数学を使用して相互相関ベクトルを計算し、次に2つの信号間の遅延を計算します。
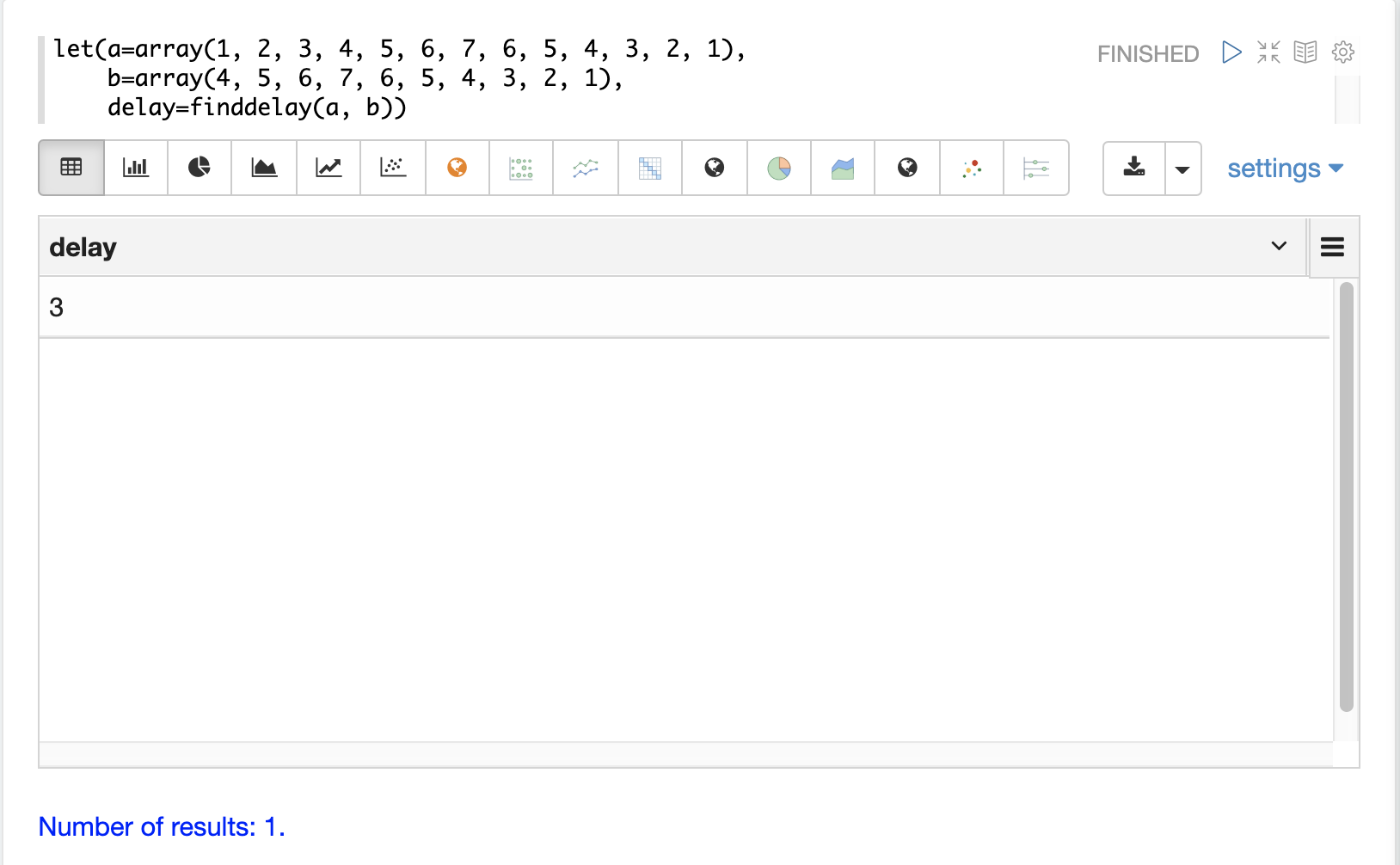
以下はfinddelay関数の例です。finddelay関数は、最初の信号と2番目の信号の間に3周期の遅延があると報告していることに注目してください。
自己相関
自己相関は、信号がそれ自体とどの程度相関しているかを測定します。自己相関は、ベクトルが信号を含むか、純粋にランダムであるかを判断するために使用されます。
いくつかの例とプロットを挙げることで、概念を理解しやすくなります。
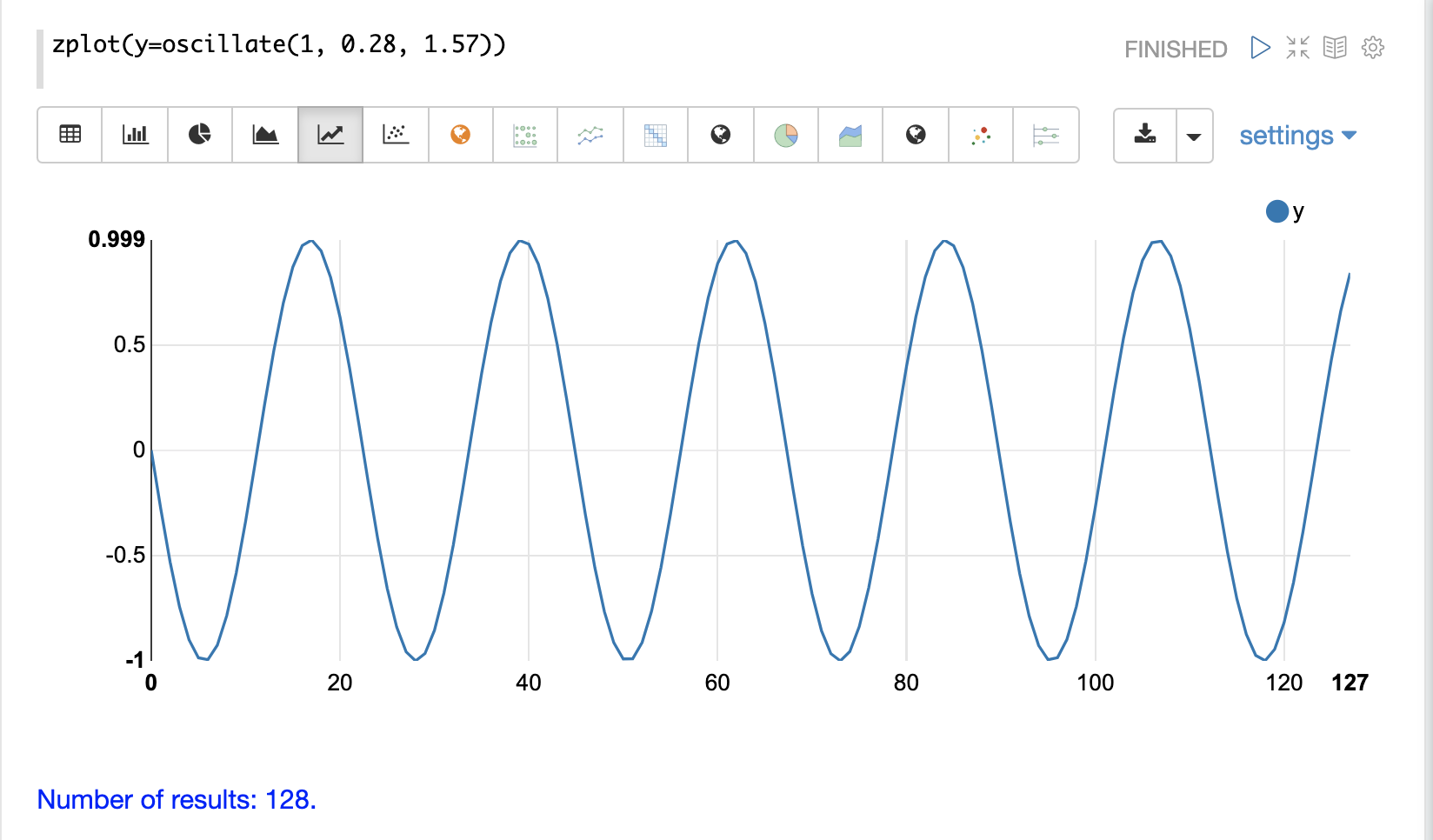
最初の例では、上記の正弦波の外挿の例を簡単に再訪します。その結果は、以下の画像にプロットされています。プロットには明らかにランダムではない構造があることに注目してください。
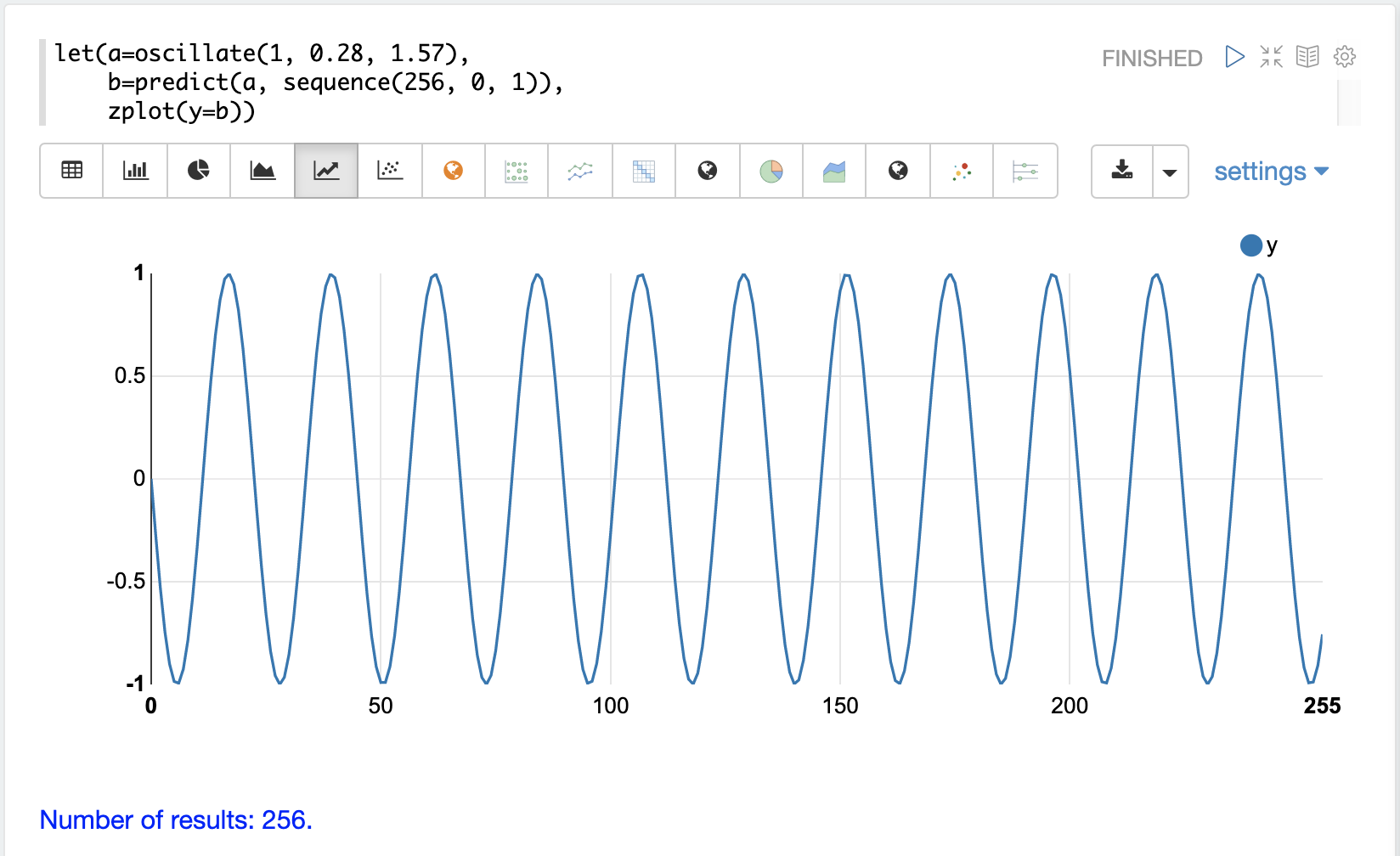
次の例では、sample関数を用いてuniformDistributionから256個のサンプルを抽出し、ランダムデータのベクトルを作成します。その結果は、以下の画像にプロットされています。データには明確な構造がなく、データはランダムに見えることに注目してください。
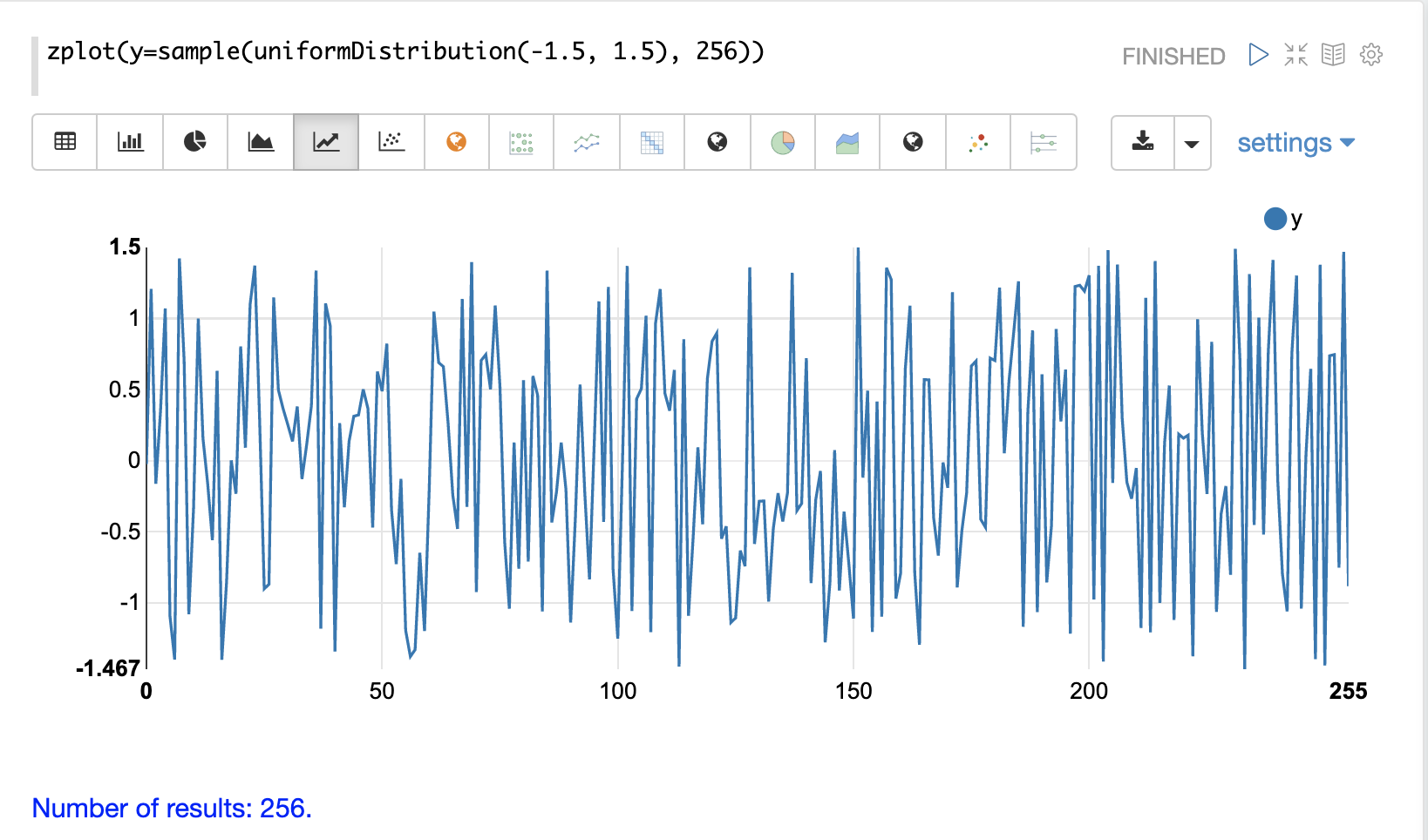
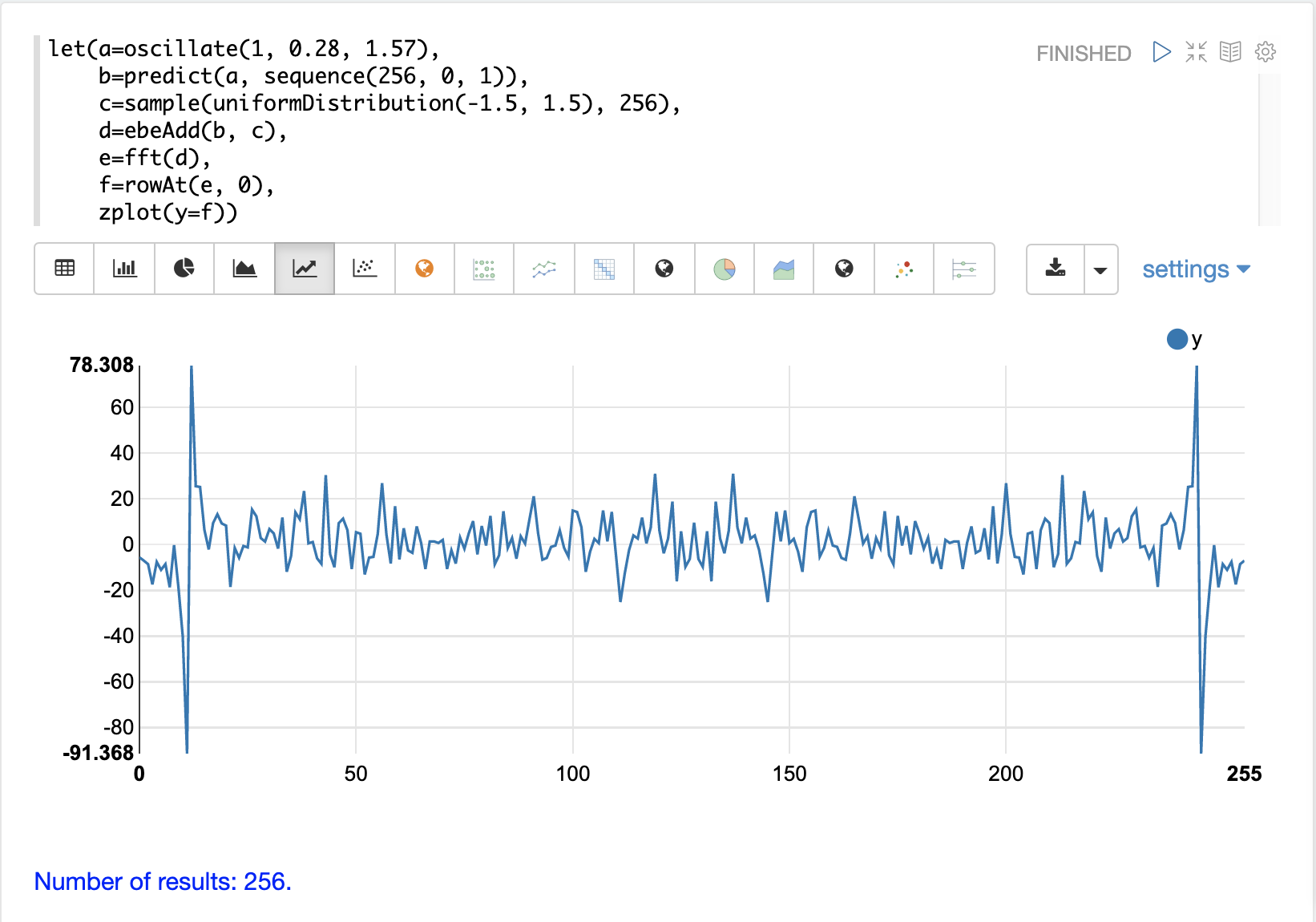
次の例では、ebeAdd関数を使用してランダムノイズを正弦波に追加します。その結果は、以下の画像にプロットされています。正弦波はノイズの中にいくらか隠されていることに注目してください。構造があるかどうかは断言できません。プロットがより密集するにつれて、ノイズの中に隠されたパターンを見つけるのが難しくなる可能性があります。
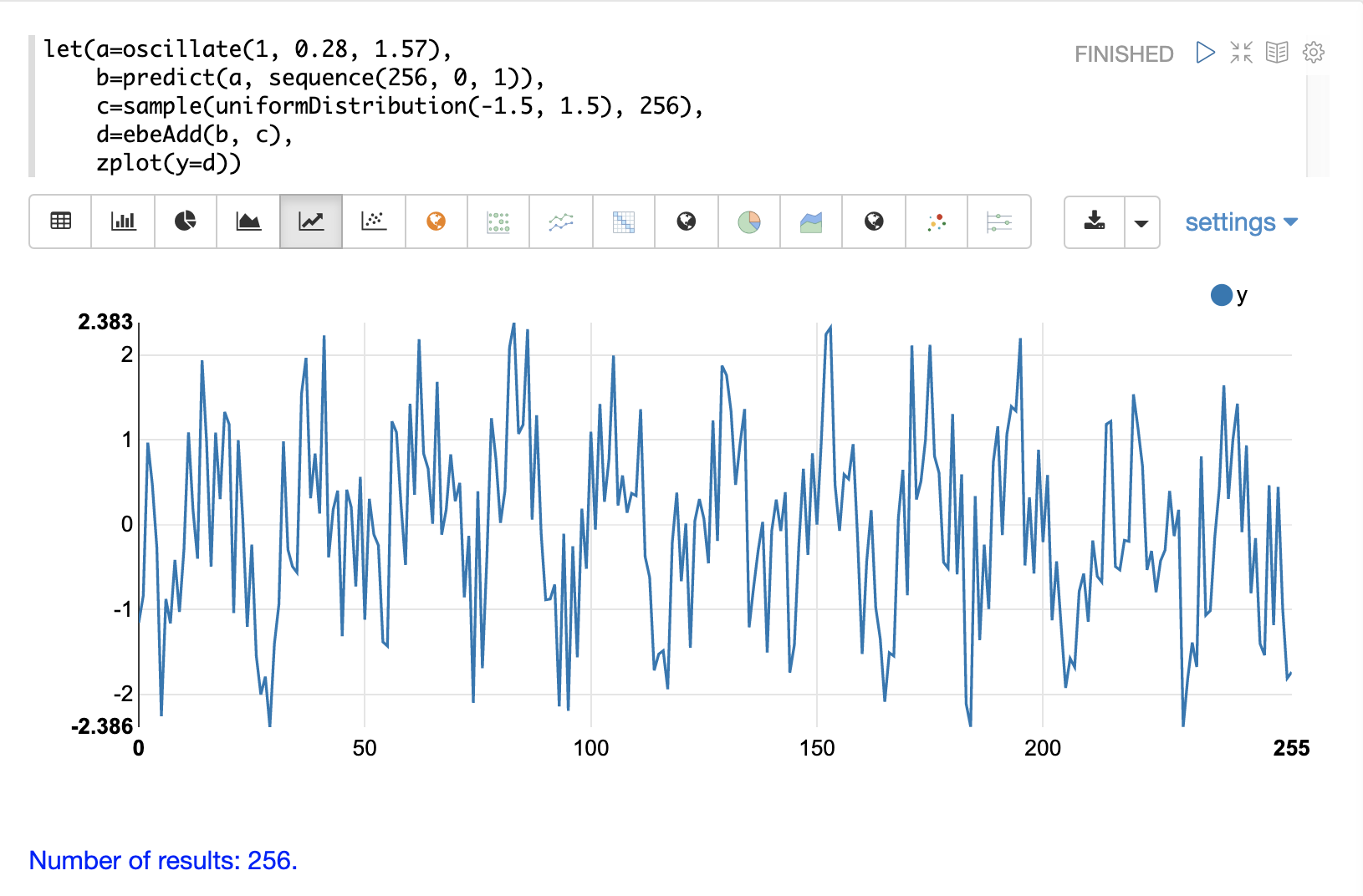
次の例では、上記の各ベクトルに対して自己相関を実行し、自己相関プロットがどうなるかを確認します。
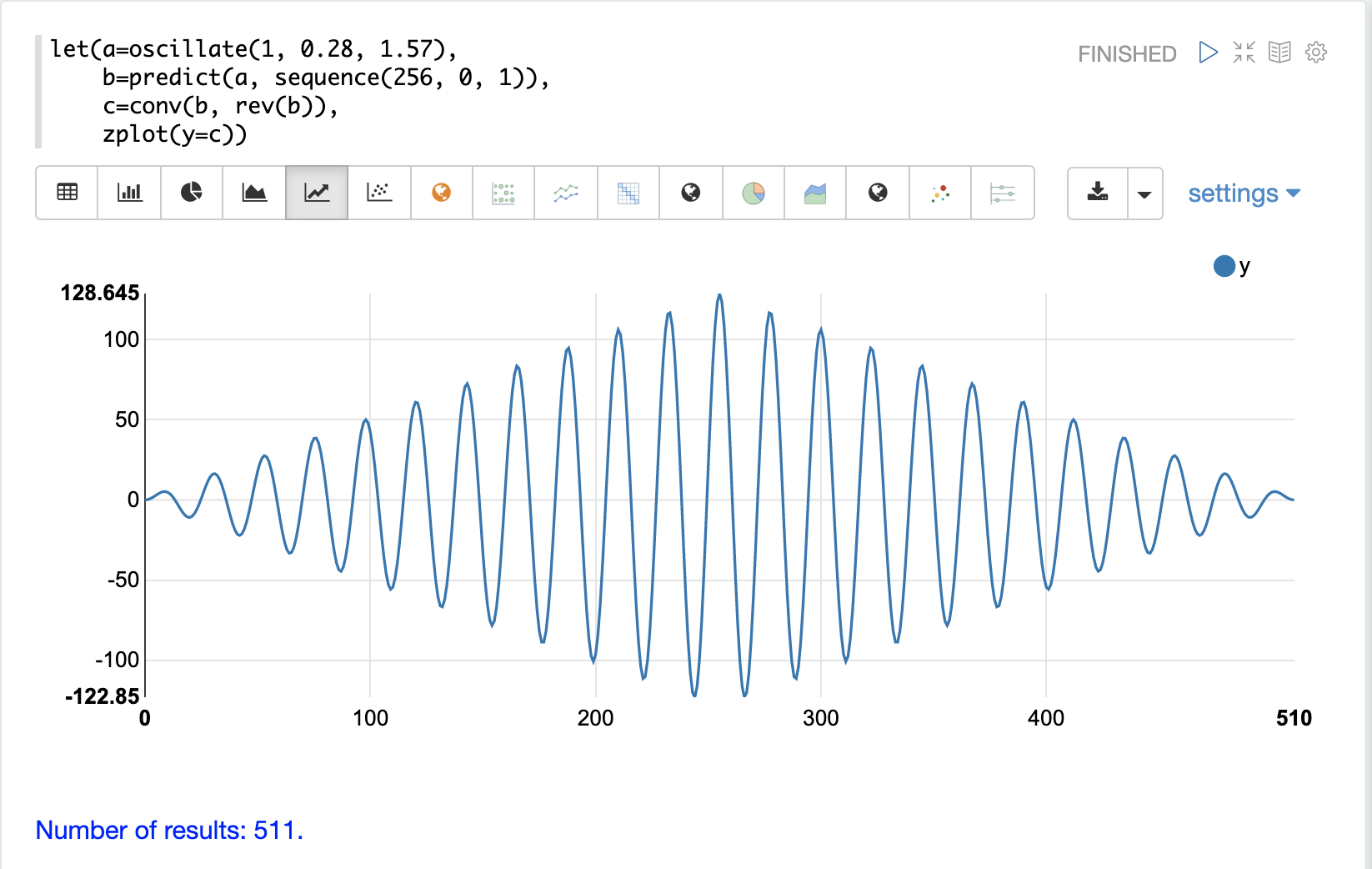
以下の例では、conv関数を用いて、正弦波である最初のベクトルの自己相関を実行しています。conv関数は、正弦波をそれ自体と相関させているだけであることに注目してください。
プロットは非常に明確な構造を持っています。正弦波をそれ自身の複製に沿ってスライドさせると、相関は強度を増しながら上下に動き、ピークに達します。このピークは中心に直接あり、正弦波が直接整列している点です。ピークの後、正弦波が直接整列している状態から離れるにつれて、相関は強度を減らしながら上下に動きます。
これは純粋な信号の自己相関プロットです。
以下の例では、純粋なノイズのベクトルで自己相関を実行しています。自己相関プロットは、正弦波とは非常に異なるプロットであることに注目してください。このプロットでは、ランダムに見える低強度の相関の長い期間があります。次に、ベクトルが直接整列している中心に高強度の相関のピークがあります。その後、低強度の相関の別の長い期間が続きます。
これは純粋なノイズの自己相関プロットです。
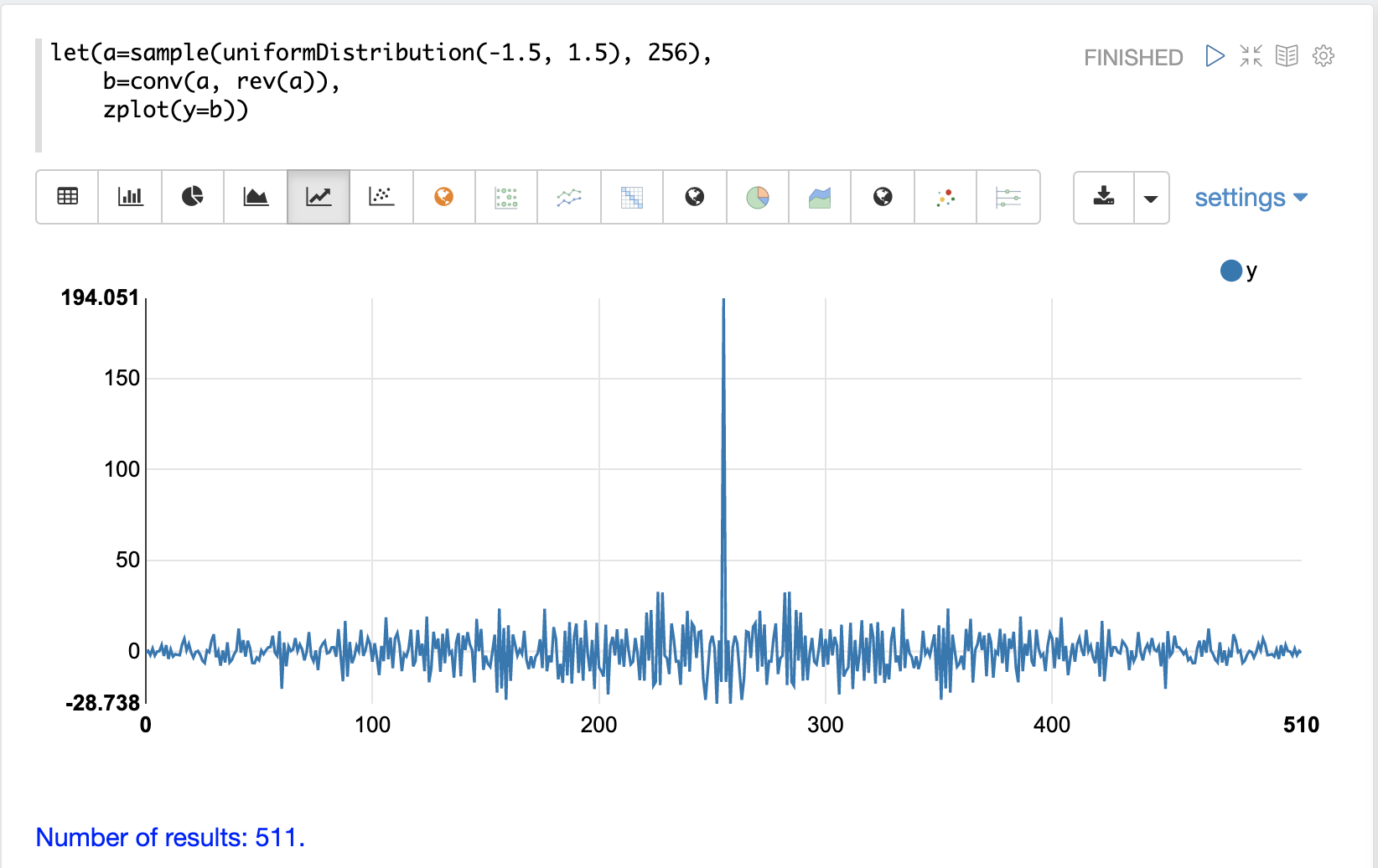
以下の例では、ノイズの中に隠された正弦波を持つベクトルで自己相関を実行しています。このプロットは、純粋な信号の自己相関プロットと同様の、非常に明確な構造の兆候を示していることに注目してください。ノイズのために相関はそれほど強くありませんが、相関プロットの形状は、ノイズの中に隠された基礎となる信号が強く示唆しています。
離散フーリエ変換
上記で説明した畳み込みベースの関数は、時間領域の信号を操作しています。時間領域では、x軸は時間、y軸は特定の時点でのある値の量です。
離散フーリエ変換は、時間領域信号を周波数領域に変換します。周波数領域では、x軸は周波数、y軸は特定の周波数における蓄積されたパワーです。
基本的な原理は、すべての時間領域信号が、異なる周波数の1つ以上の信号(正弦波)で構成されていることです。離散フーリエ変換は、時間領域信号を構成周波数に分解し、各周波数のパワーを測定します。
離散フーリエ変換には多くの重要な用途があります。以下の例では、離散フーリエ変換を使用して、信号に構造があるか、純粋にランダムであるかを判断します。
複素数の結果
fft関数は、**実数**データのベクトルに対して離散フーリエ変換を実行します。fft関数の結果は、**複素数**として返されます。複素数は、**実数**部と**虚数**部の2つの部分を持っています。結果の**実数**部は、さまざまな周波数における信号の大きさを表します。結果の**虚数**部は**位相**を表します。以下の例では、結果の**実数**部分のみを扱います。
fft関数は、2行の行列を返します。行列の最初の行は、複素数の結果の**実数**部分です。行列の2番目の行は、複素数の結果の**虚数**部分です。rowAt関数は、行にアクセスしてベクトルとして処理するために使用できます。
高速フーリエ変換の例
最初の例では、自己相関の例で使用されている正弦波に対してfft関数を呼び出しています。
fft関数の結果は行列です。rowAt関数は、fft応答の実数値を含むベクトルである行列の最初の行を返すために使用されます。
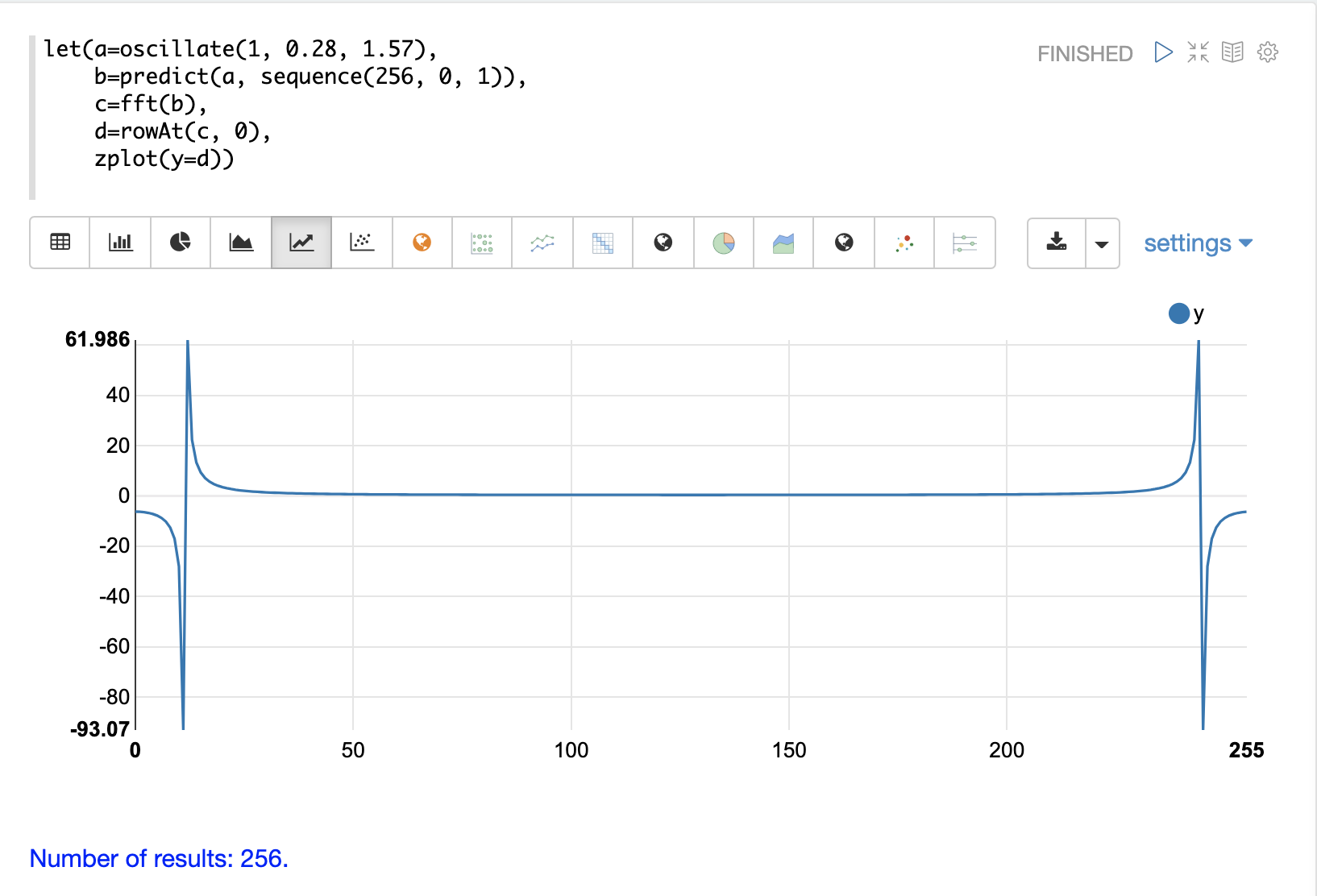
fft応答の実数値のプロットを以下に示します。プロットの反対側に2つのピークがあることに注目してください。プロットは実際にはミラーリングされた応答を示しています。プロットの右側が左側の正確なミラーであることは、実数データではなく複素数データに対してfftを実行した場合に予想されます。
また、fftが単一のピークにかなりのパワーを蓄積していることに注目してください。これは、正弦波の特定の周波数に関連付けられたパワーです。プロット内のほとんどの周波数は、それに関連付けられたパワーがほぼ0です。このfftは、ノイズレベルが非常に低い明確な信号を示しています。
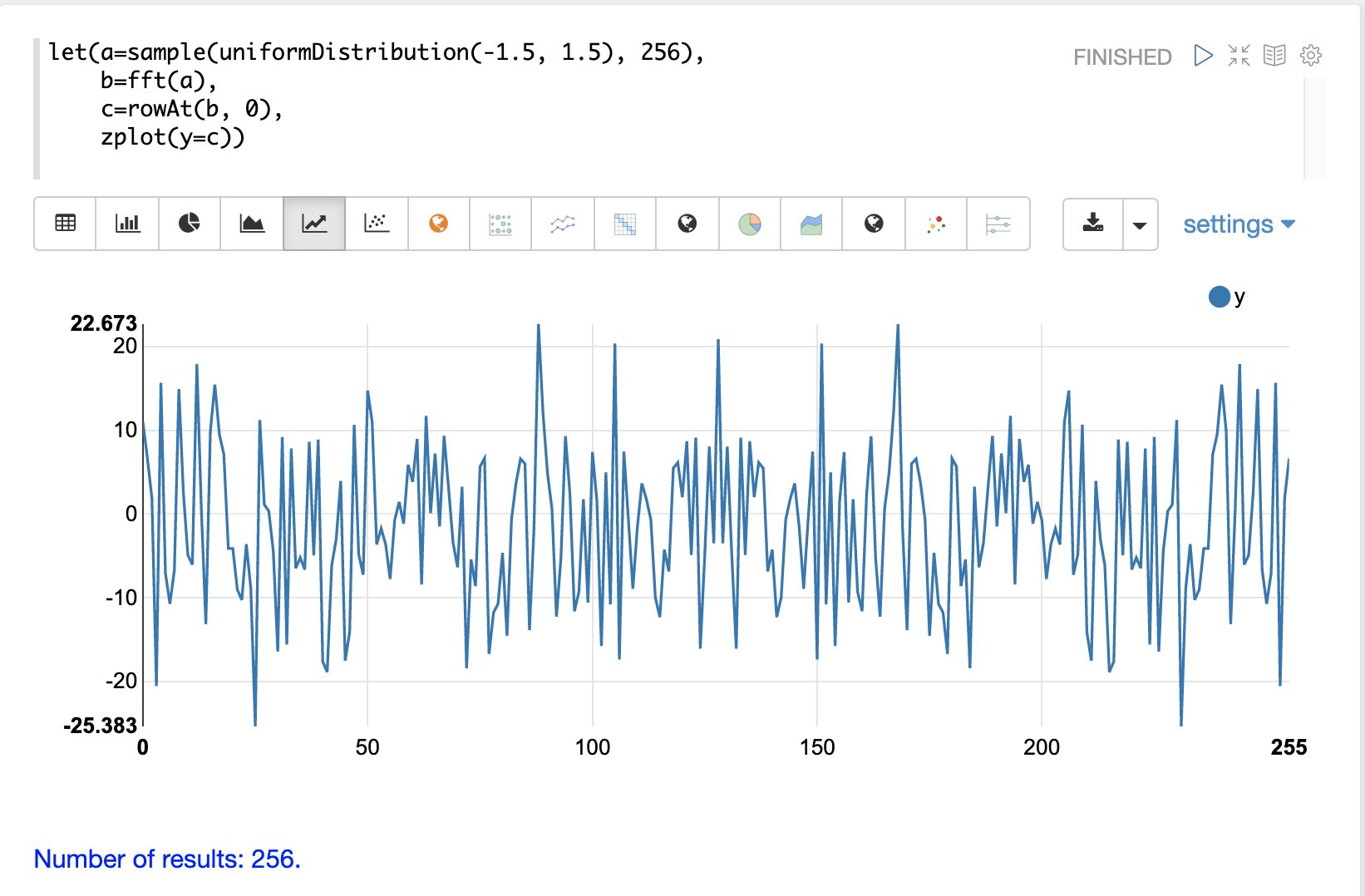
2番目の例では、自己相関の例で使用したものと同様のランダムデータのベクトルに対してfft関数を呼び出しています。fft応答の実数値のプロットを以下に示します。
この応答では、明確なピークがないことに注目してください。代わりに、すべての周波数がランダムなレベルのパワーを蓄積しています。このfftは、信号の明確な兆候を示しておらず、ノイズのように見えます。
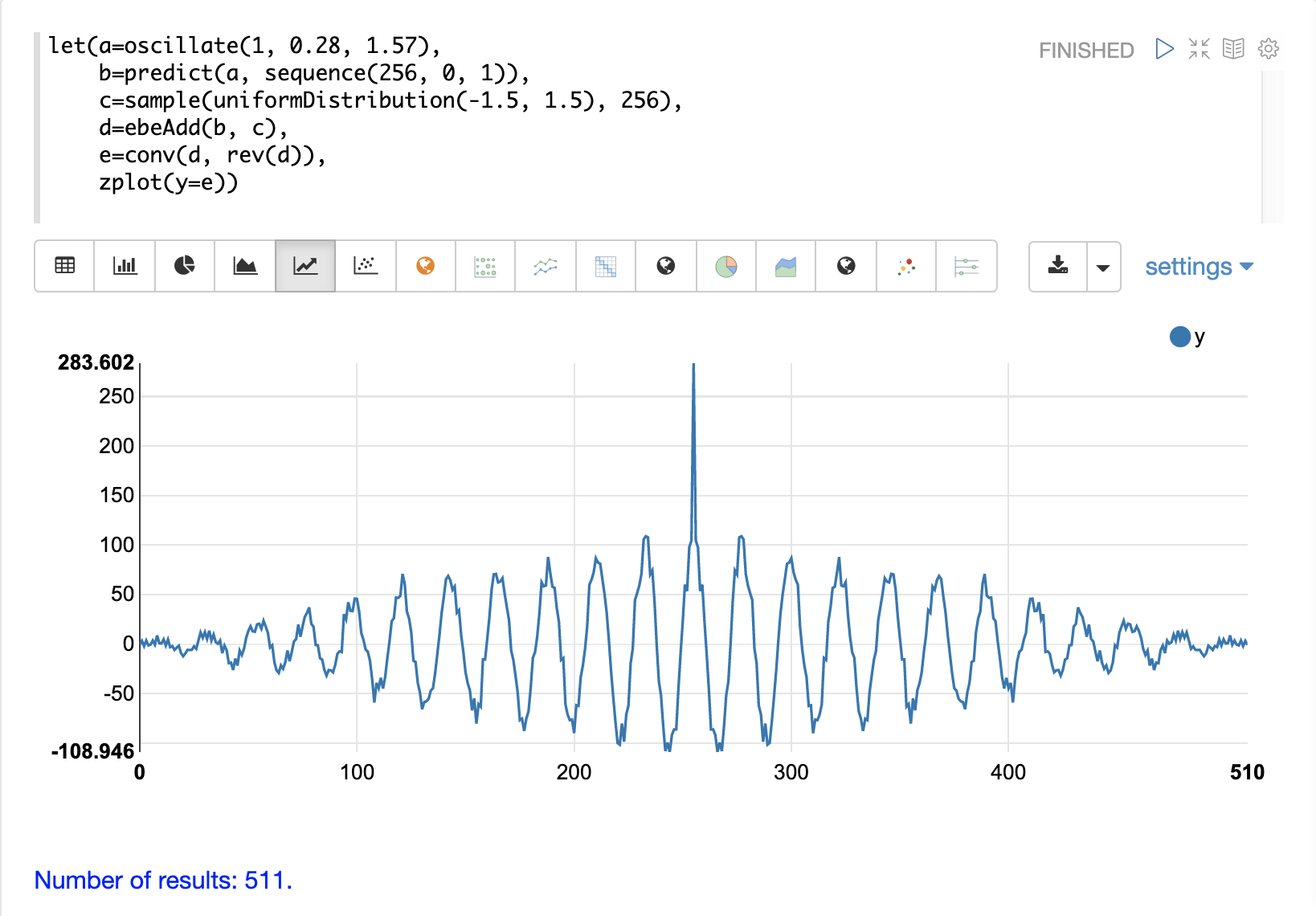
3番目の例では、自己相関の例で使用したものと同じ、ノイズの中に隠された信号に対してfft関数を呼び出しています。
fftの純粋な信号と同じ位置に、2つの明確なミラーリングされたピークがあることに注目してください。しかし、周波数にもかなりのノイズがあります。fftは信号を見つけており、信号とともにかなりのノイズもあることを示しています。