確率分布

このユーザーガイドのセクションでは、数式ライブラリに含まれる確率分布フレームワークについて説明します。

可視化

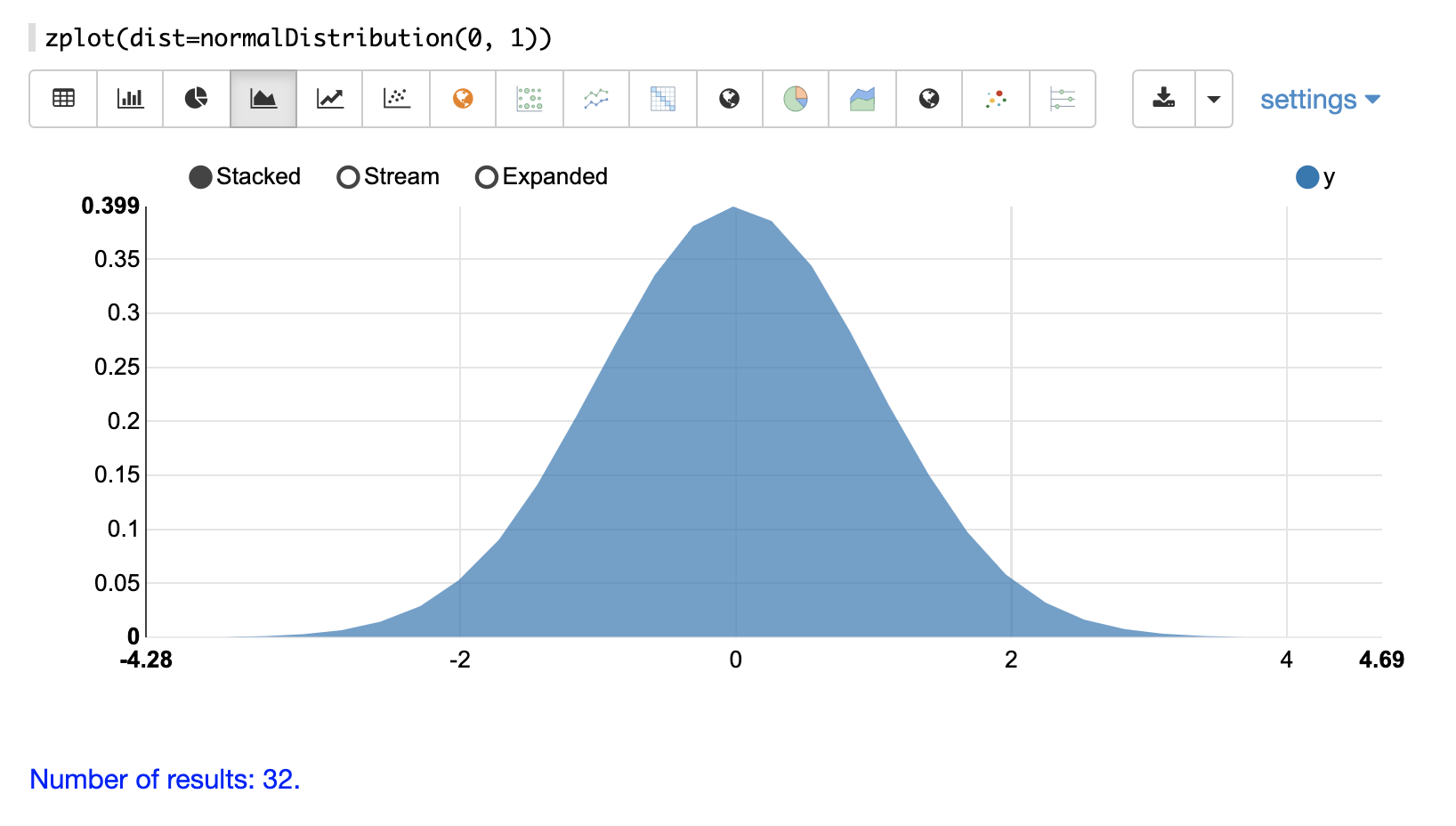
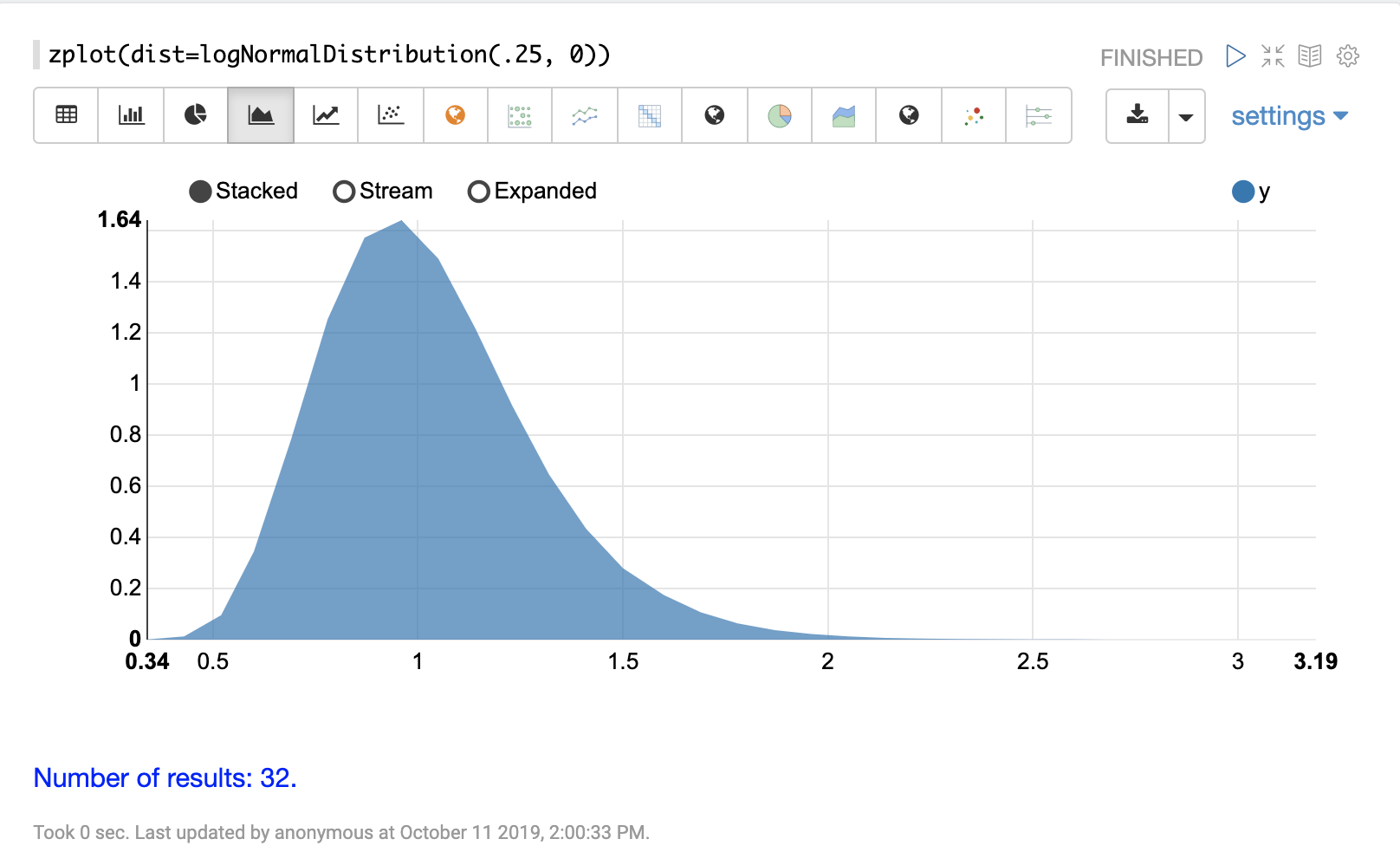
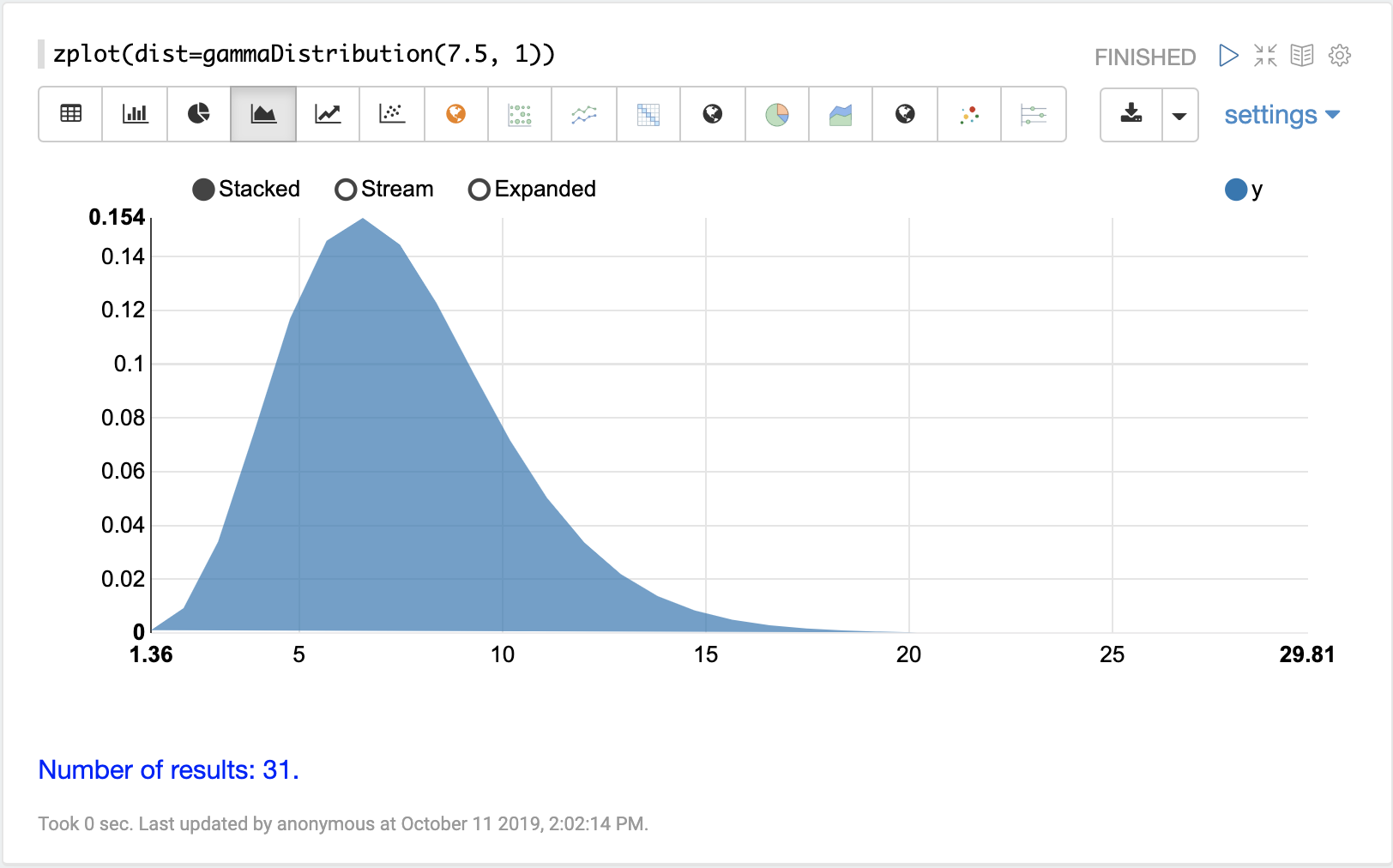
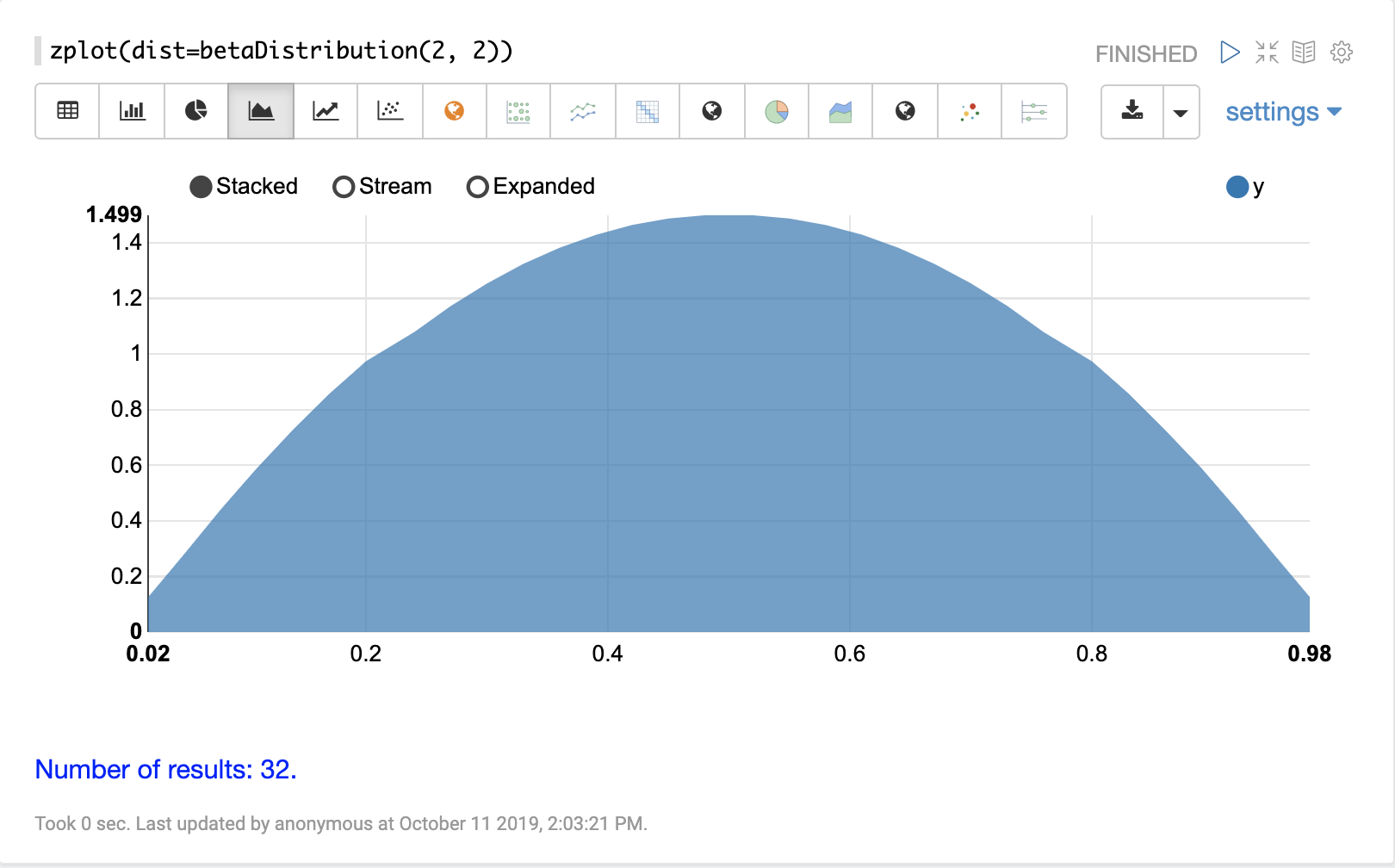
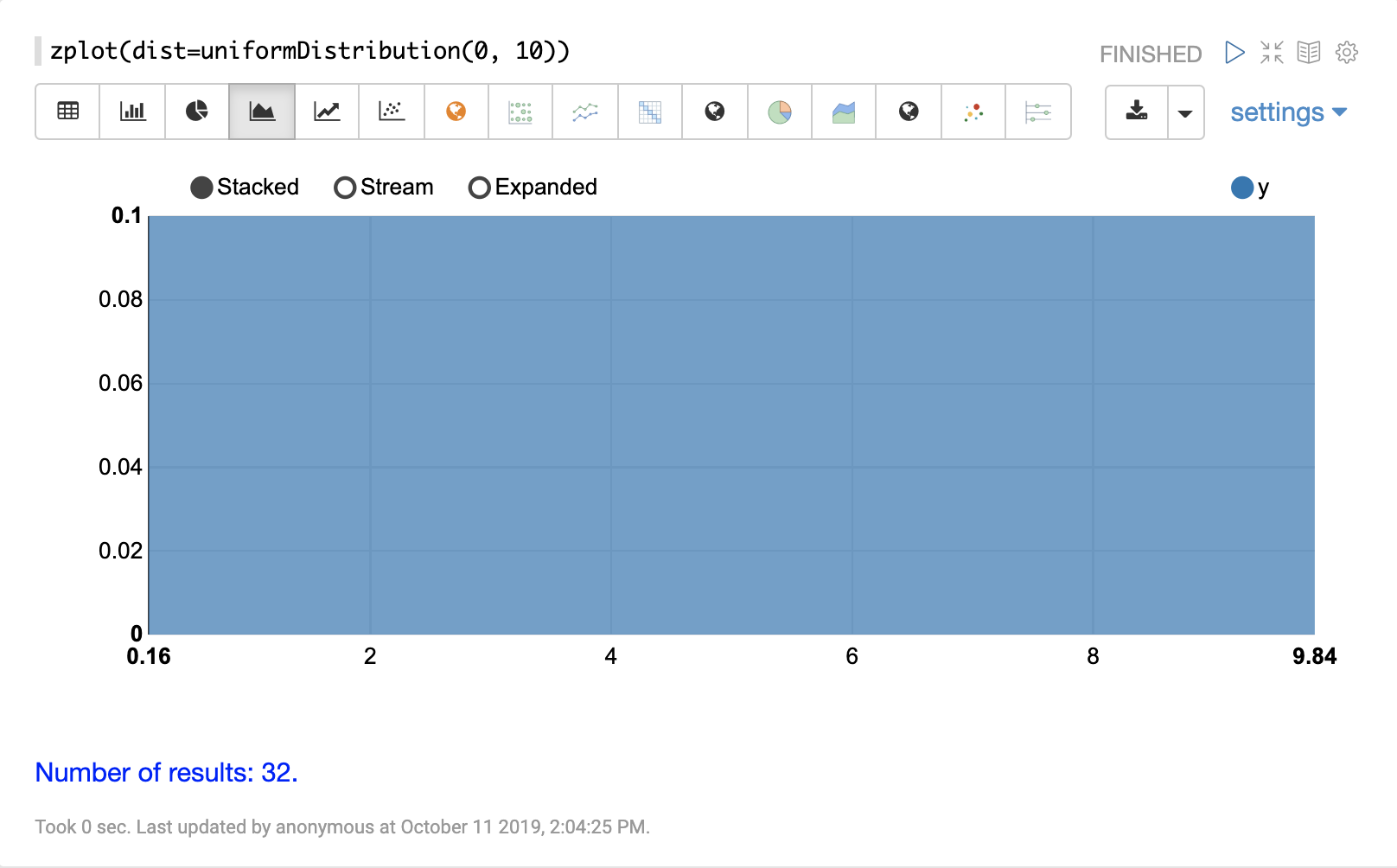
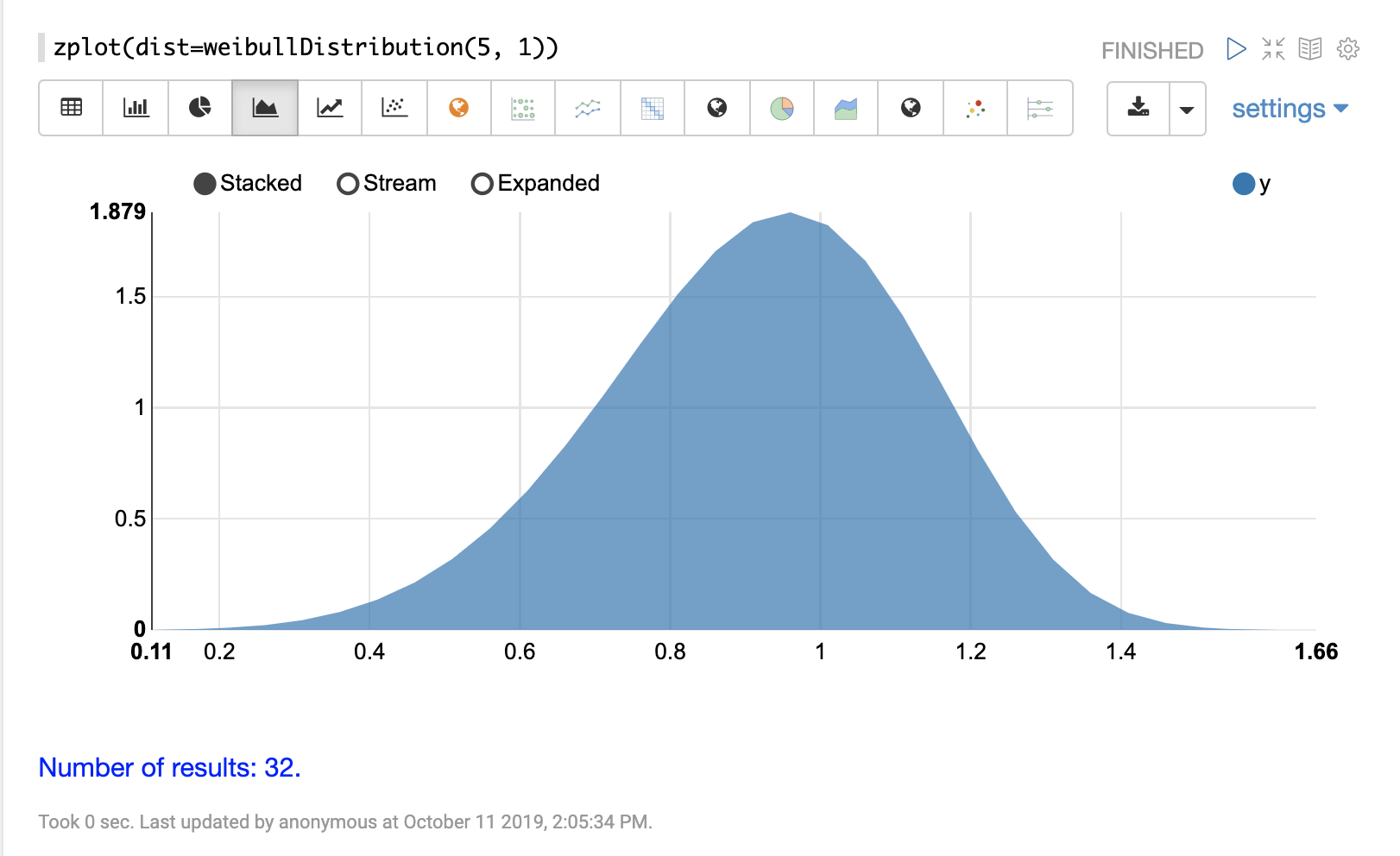
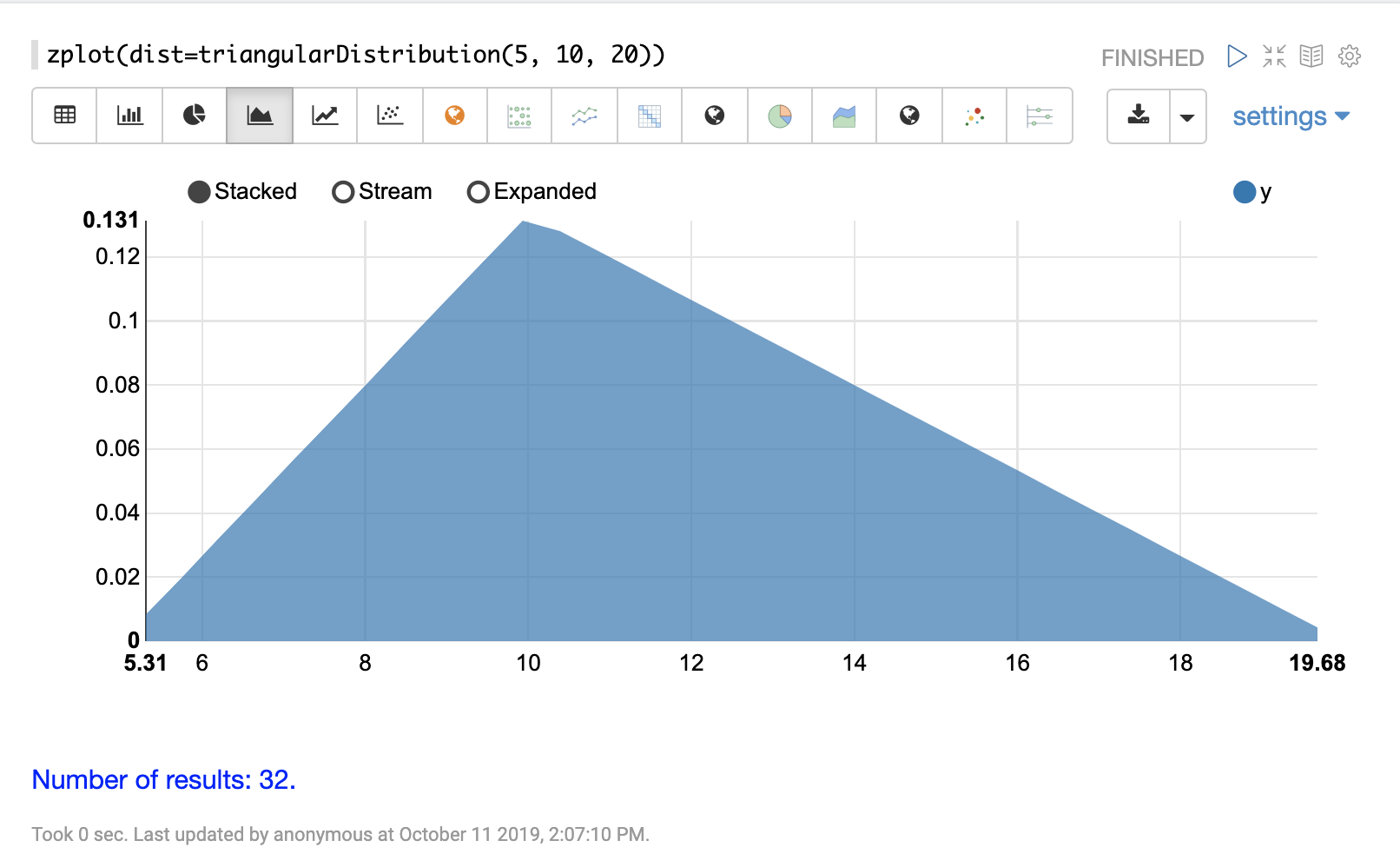
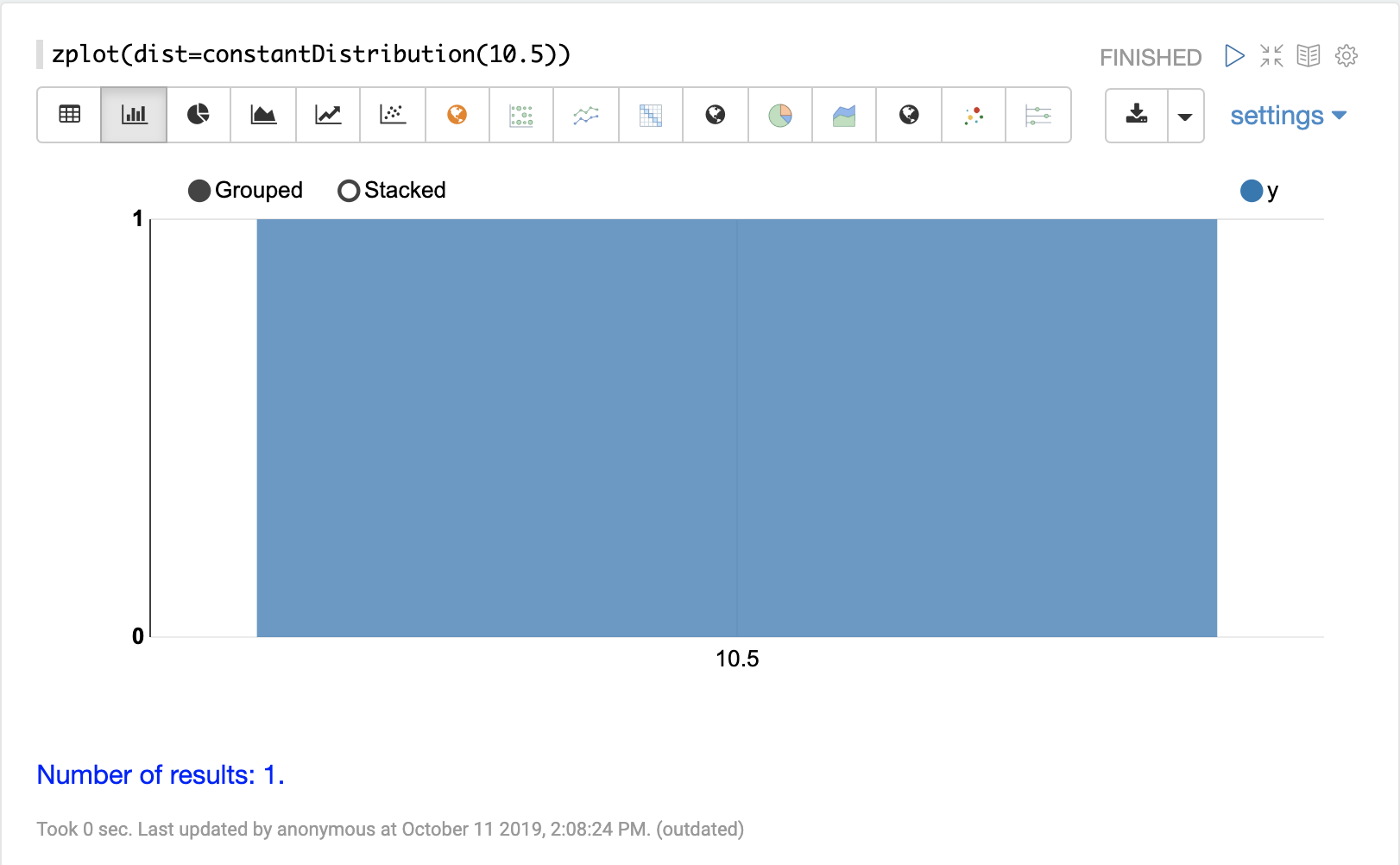
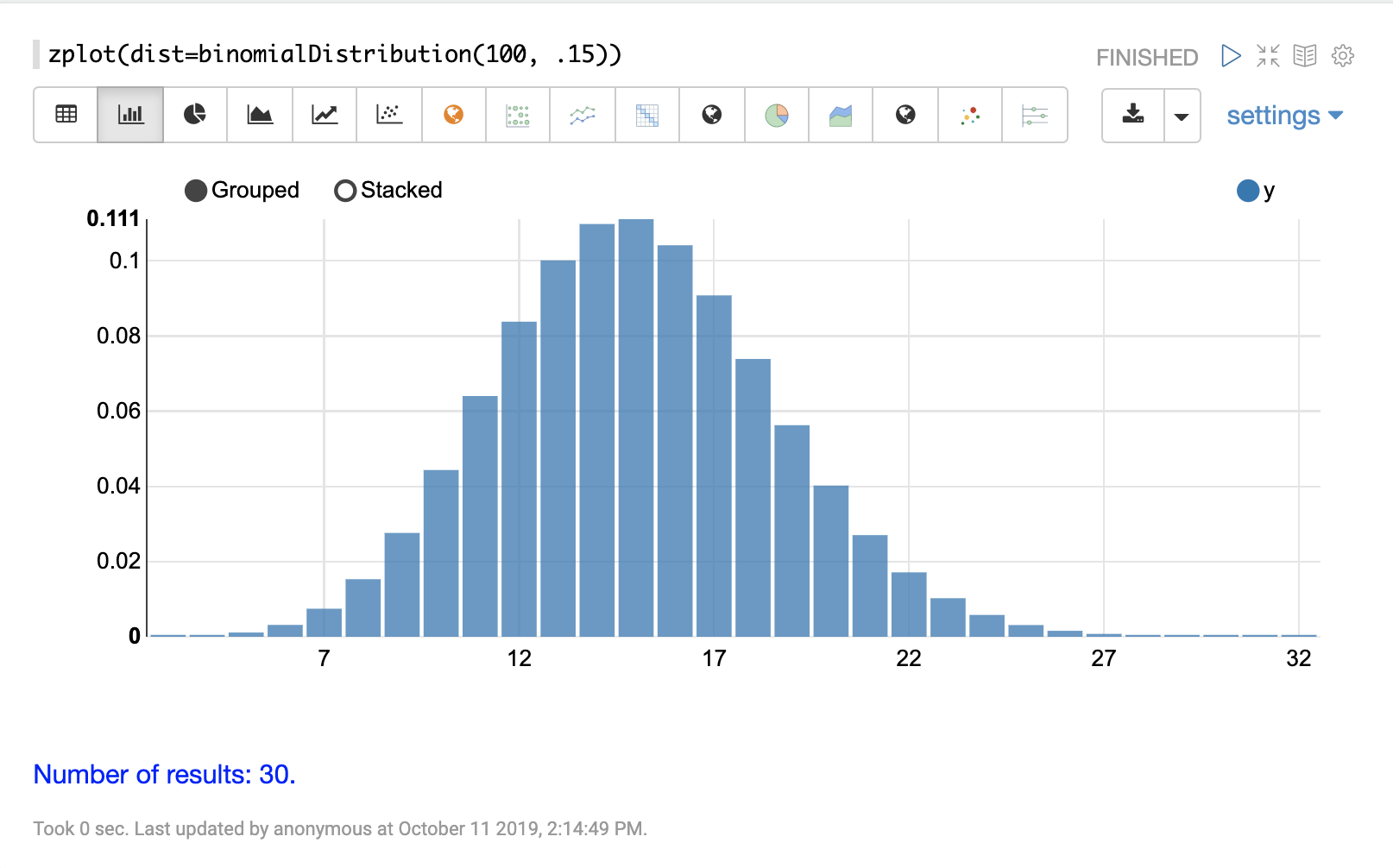
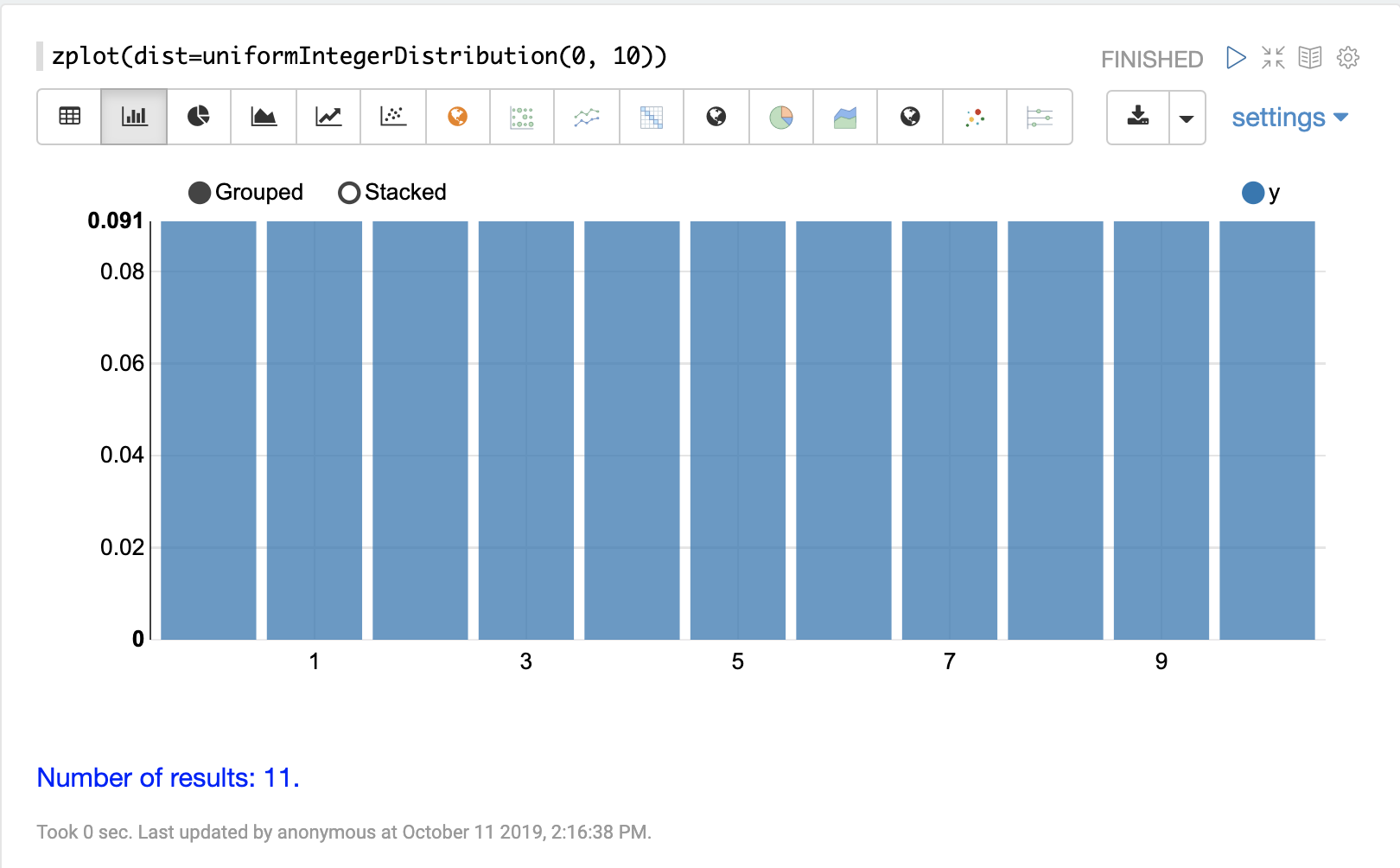
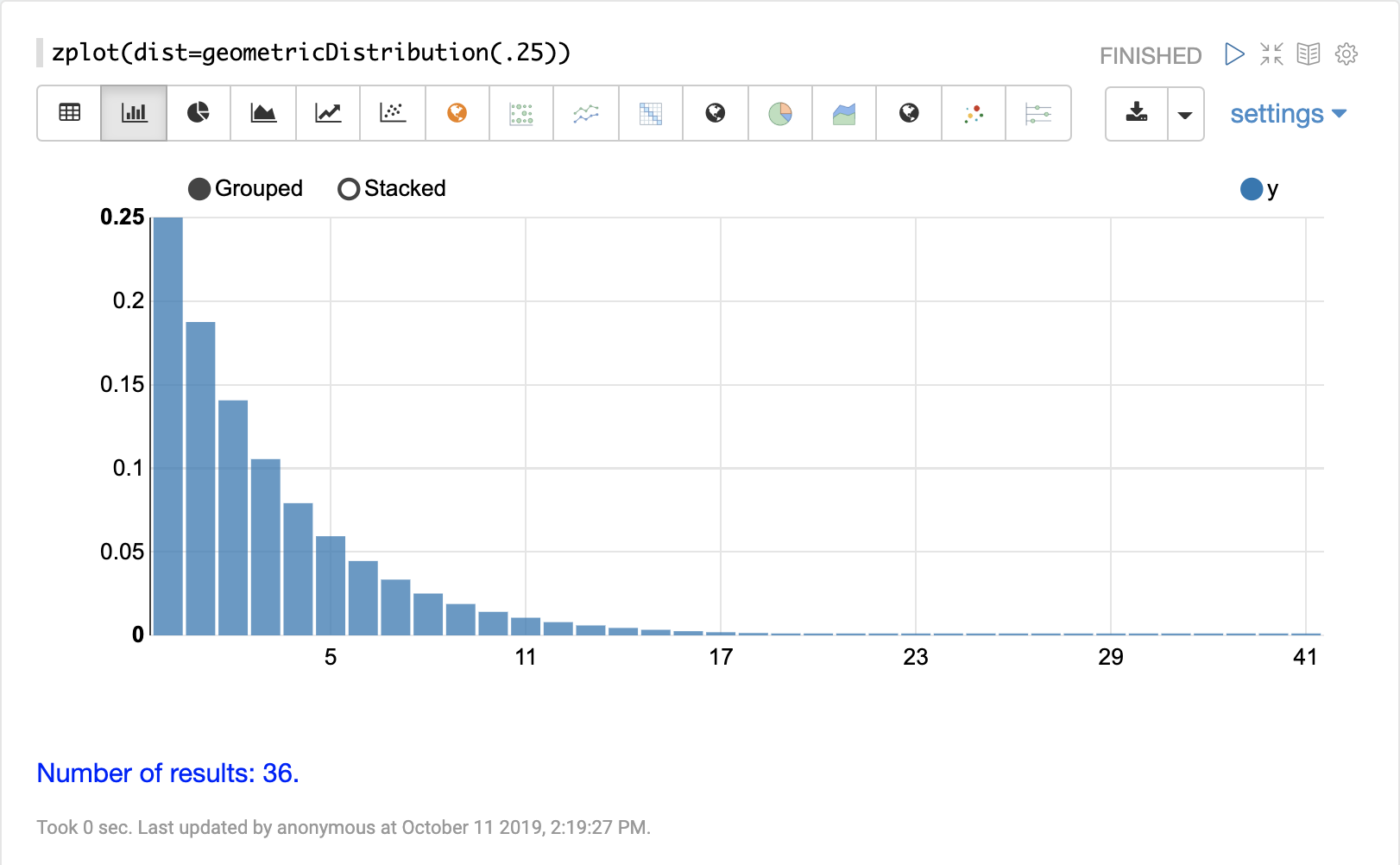
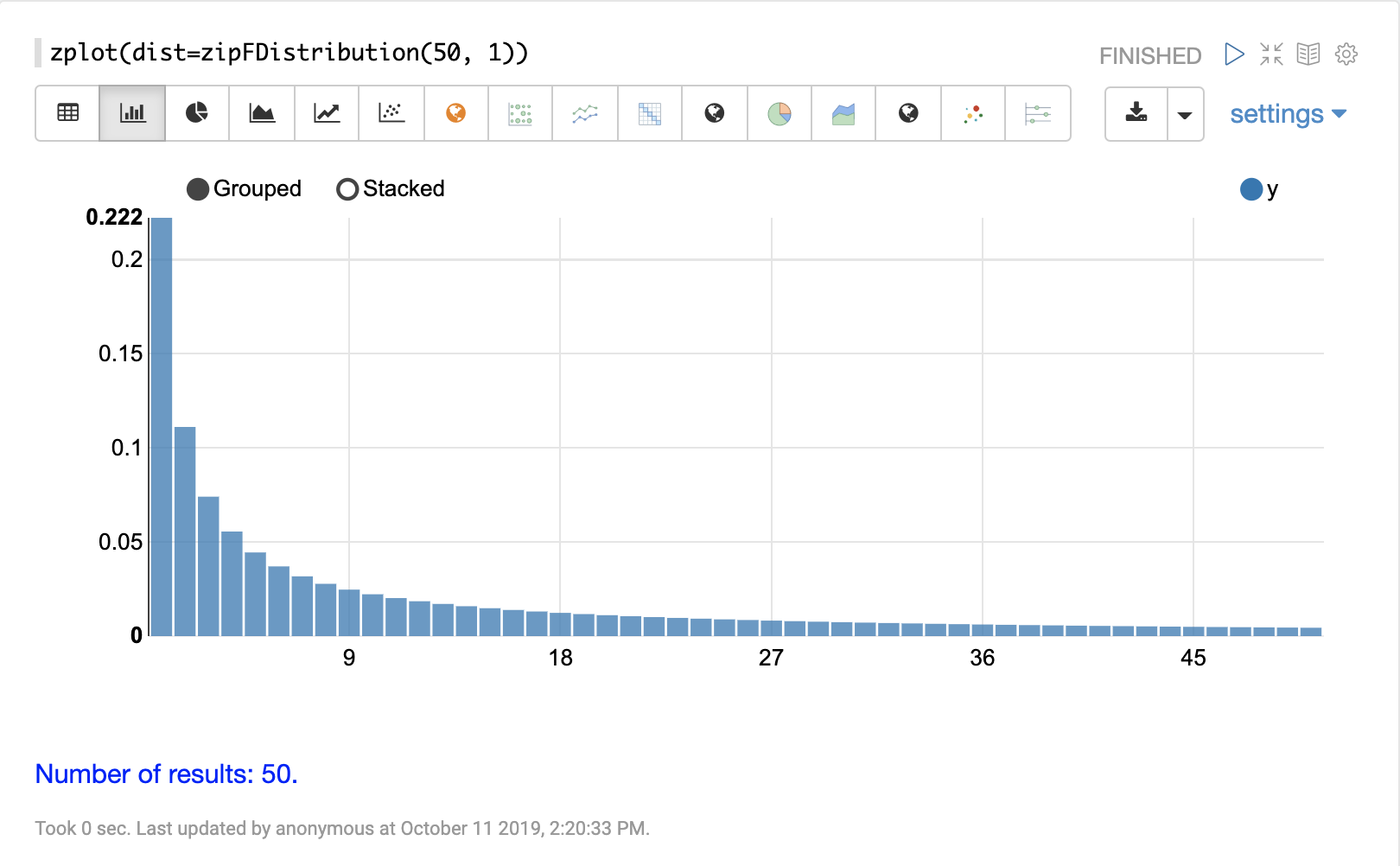
確率分布は、分布の確率密度関数 (PDF) を可視化する dist パラメータを持つ zplot 関数を使用して、Zeppelin-Solr で可視化できます。

以下の各分布に、可視化の例を示します。

連続分布

連続確率分布は、連続した数値 (浮動小数点) で機能します。以下に、サポートされている連続確率分布を示します。

empiricalDistribution

empiricalDistribution 関数は、実際のデータから連続確率分布を作成します。

経験的分布は、SolrCloud コレクションからのランダムサンプルの確率密度関数を便利に可視化するために使用できます。以下の例は、32 ビンヒストグラムを使用したランダムサンプルの確率密度を可視化する zplot 関数を示しています。

$empirical$

normalDistribution

以下の可視化は、mean が 0、standard deviation が 1 の正規分布を示しています。

$dist$

logNormalDistribution

以下の可視化は、shape が .25、scale が 0 の対数正規分布を示しています。

$lognormal$

gammaDistribution

以下の可視化は、shape が 7.5、scale が 1 のガンマ分布を示しています。

$gamma$

betaDistribution

以下の可視化は、shape1 が 2、shape2 が 2 のベータ分布を示しています。

$beta$

uniformDistribution

以下の可視化は、0 から 10 の間の均一分布を示しています。

$uniformr$

weibullDistribution

以下の可視化は、shape が 5、scale が 1 のワイブル分布を示しています。

$weibull$

triangularDistribution

以下の可視化は、最小値が 5、最頻値が 10、最大値が 20 の三角分布を示しています。

$triangular$

constantDistribution

以下の可視化は、10.5 の定数分布を示しています。

$constant$

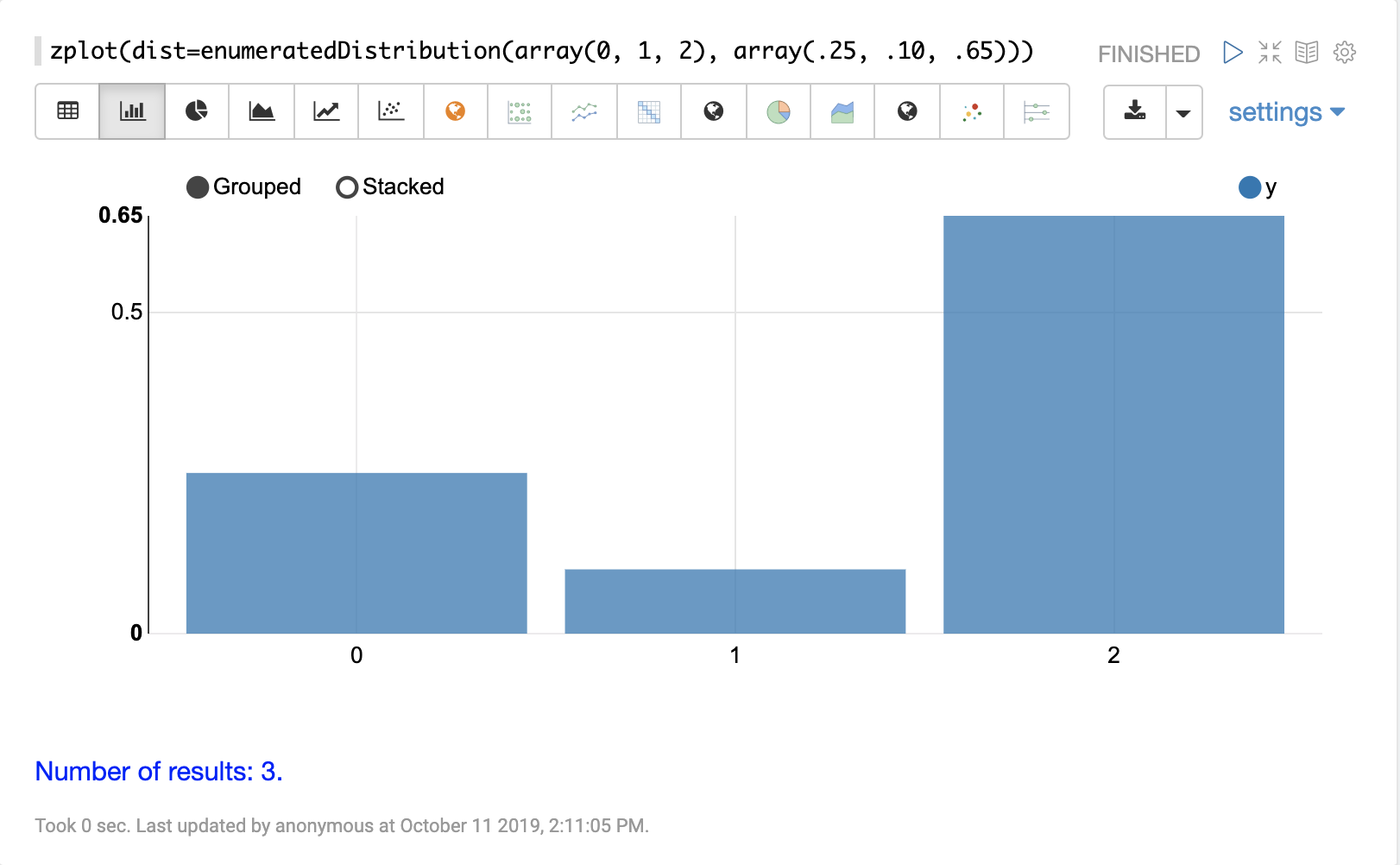
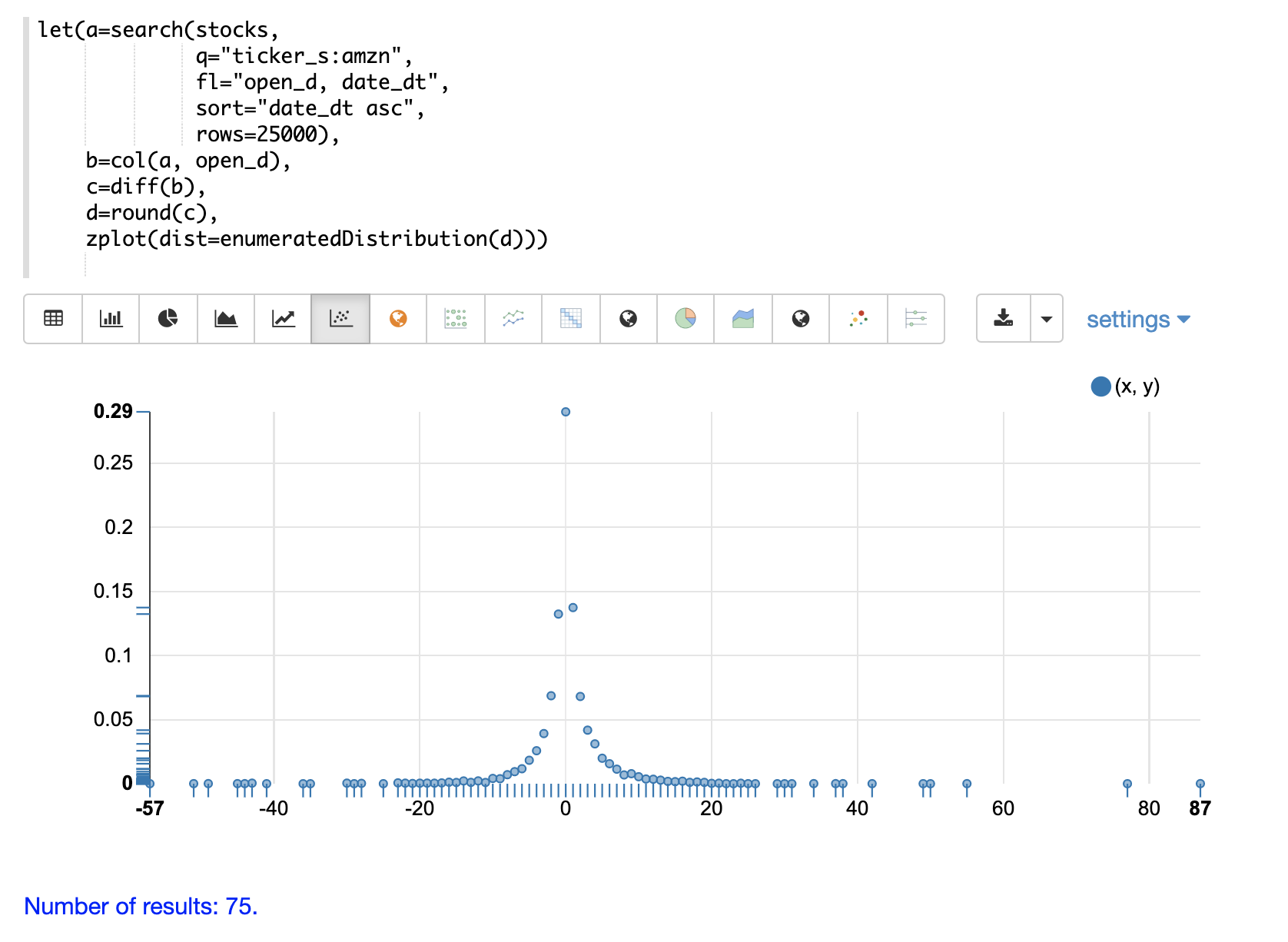
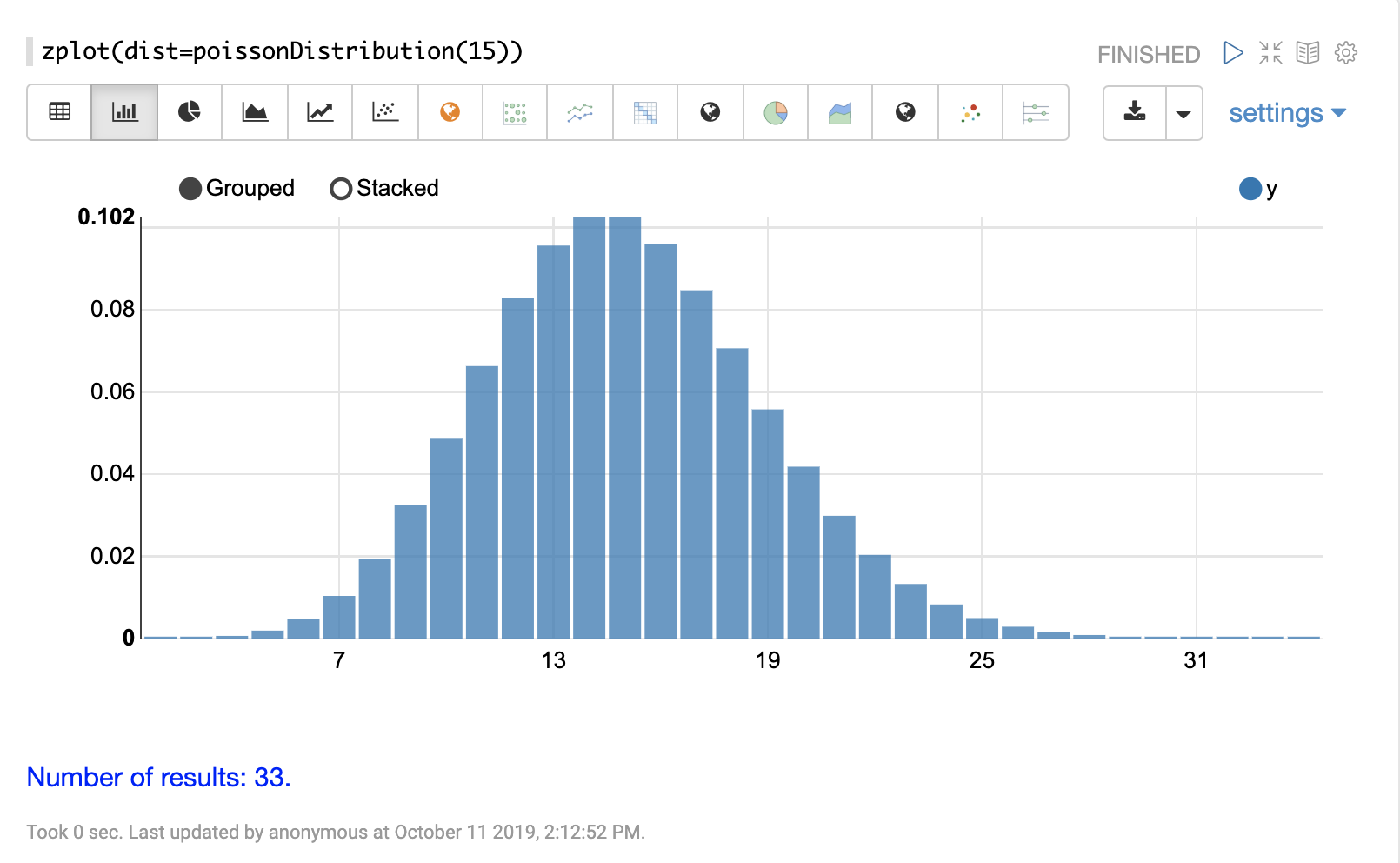
離散分布

離散確率分布は、離散数値 (整数) で機能します。以下に、サポートされている離散確率分布を示します。

enumeratedDistribution

enumeratedDistribution 関数は、列挙された値と確率のリストから、または離散値のデータセットから離散分布関数を作成します。

以下の可視化は、離散値と確率のリストから作成された列挙分布を示しています。

$enum1$

以下の可視化は、離散値のベクトルに変換された検索結果から生成された列挙分布を示しています。

$enum2$

poissonDistribution

以下の可視化は、平均が15のポアソン分布を示しています。

$poisson$

二項分布

以下の可視化は、試行回数100、成功確率0.15の二項分布を示しています。

$binomial$

一様整数分布

以下の可視化は、0から10までの一様整数分布を示しています。

$uniform$

幾何分布

以下の可視化は、成功確率が0.25の幾何分布を示しています。

$geometric$

ジップ分布

以下の可視化は、サイズが50、指数が1のジップ分布を示しています。

$zipf$

累積確率

cumulativeProbability関数は、特定の分布内で特定の確率変数が現れる累積確率を計算するために、すべての確率分布で使用できます。

以下は、正規分布内の確率変数の累積確率を計算する例です。

let(a=normalDistribution(10, 5),
    b=cumulativeProbability(a, 12))

この例では、平均10、標準偏差5の正規分布関数が作成されます。次に、この特定の分布に対して値12の累積確率が計算されます。

この式が/streamハンドラーに送信されると、以下が返されます。

{
  "result-set": {
    "docs": [
      {
        "b": 0.6554217416103242
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

確率

すべての確率分布は、値の範囲間の確率を計算できます。

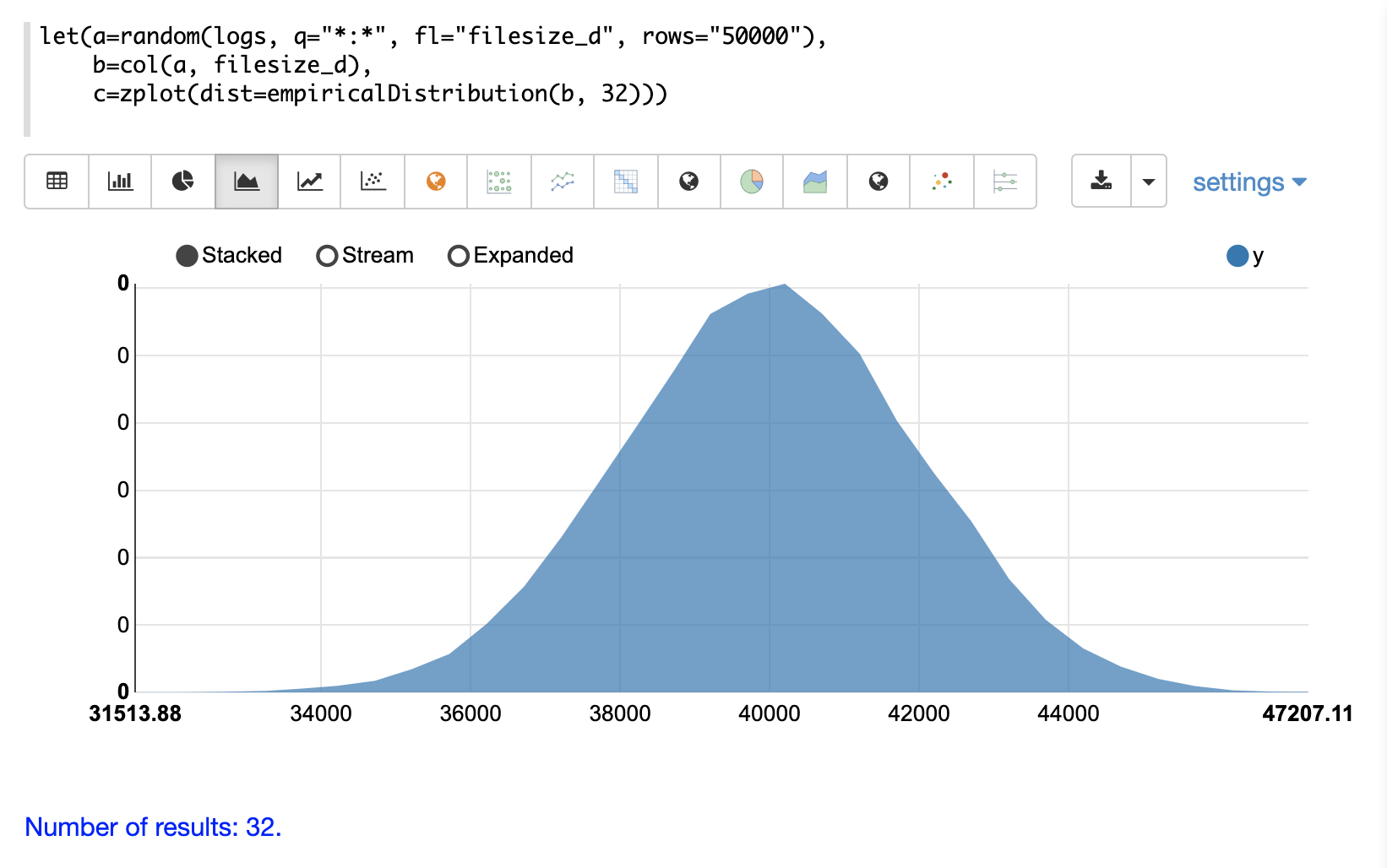
次の例では、ログコレクションから抽出されたファイルサイズのサンプルから経験分布が作成されます。次に、40000から41000までのファイルサイズの確率が19％と計算されます。

let(a=random(logs, q="*:*", fl="filesize_d", rows="50000"),
    b=col(a, filesize_d),
    c=empiricalDistribution(b, 100),
    d=probability(c, 40000, 41000))

この式が/streamハンドラーに送信されると、以下が返されます。

{
  "result-set": {
    "docs": [
      {
        "d": 0.19006540560734791
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 550
      }
    ]
  }
}

離散確率

probability関数は、任意の離散分布関数で使用して、離散値の確率を計算できます。

以下は、ポアソン分布内の離散値の確率を計算する例です。

この例では、平均が100のポアソン分布関数が作成されます。次に、この特定の分布に対して、離散値101のサンプルが現れる確率が計算されます。

let(a=poissonDistribution(100),
    b=probability(a, 101))

この式が/streamハンドラーに送信されると、以下が返されます。

{
  "result-set": {
    "docs": [
      {
        "b": 0.039466333474403106
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

サンプリング

すべての確率分布はサンプリングをサポートしています。sample関数は、確率分布から1つ以上のランダムサンプルを返します。

以下は、正規分布から単一のサンプルを抽出する例です。

let(a=normalDistribution(10, 5),
    b=sample(a))

この式が/streamハンドラーに送信されると、以下が返されます。

{
  "result-set": {
    "docs": [
      {
        "b": 11.24578055004963
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 0
      }
    ]
  }
}

sample関数は、サンプルのベクトルを返すこともできます。サンプルのベクトルは、散布図として可視化して、基礎となる分布を直感的に理解することができます。

最初の例は、平均0、標準偏差5の正規分布の散布図を示しています。

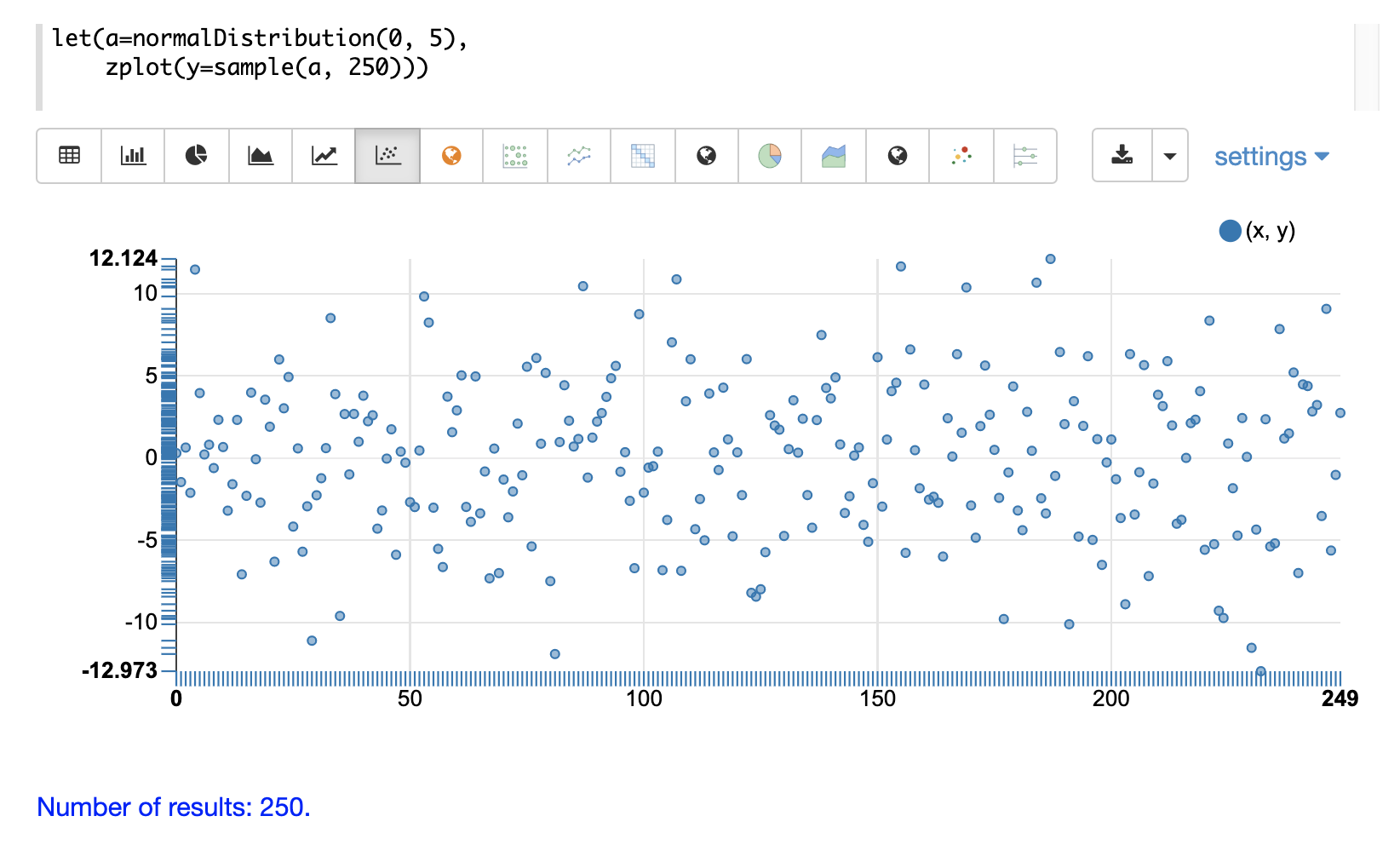
$sample scatter$

次の例は、サンプルベクトルに昇順ソートを適用した、同じ分布の散布図を示しています。

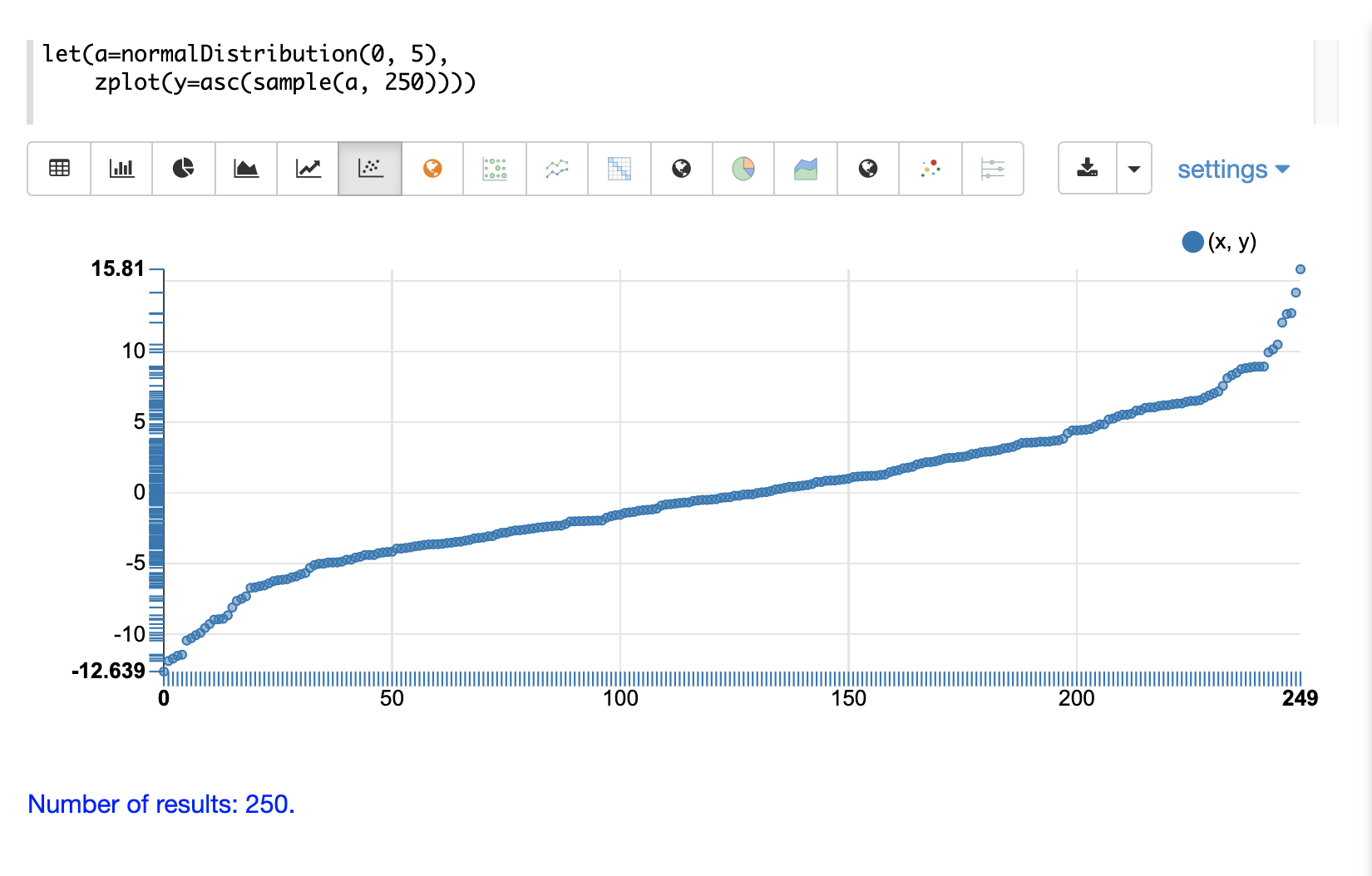
$sample scatter1$

次の例は、同じ散布図に重ねて表示された2つの異なる分布を示しています。

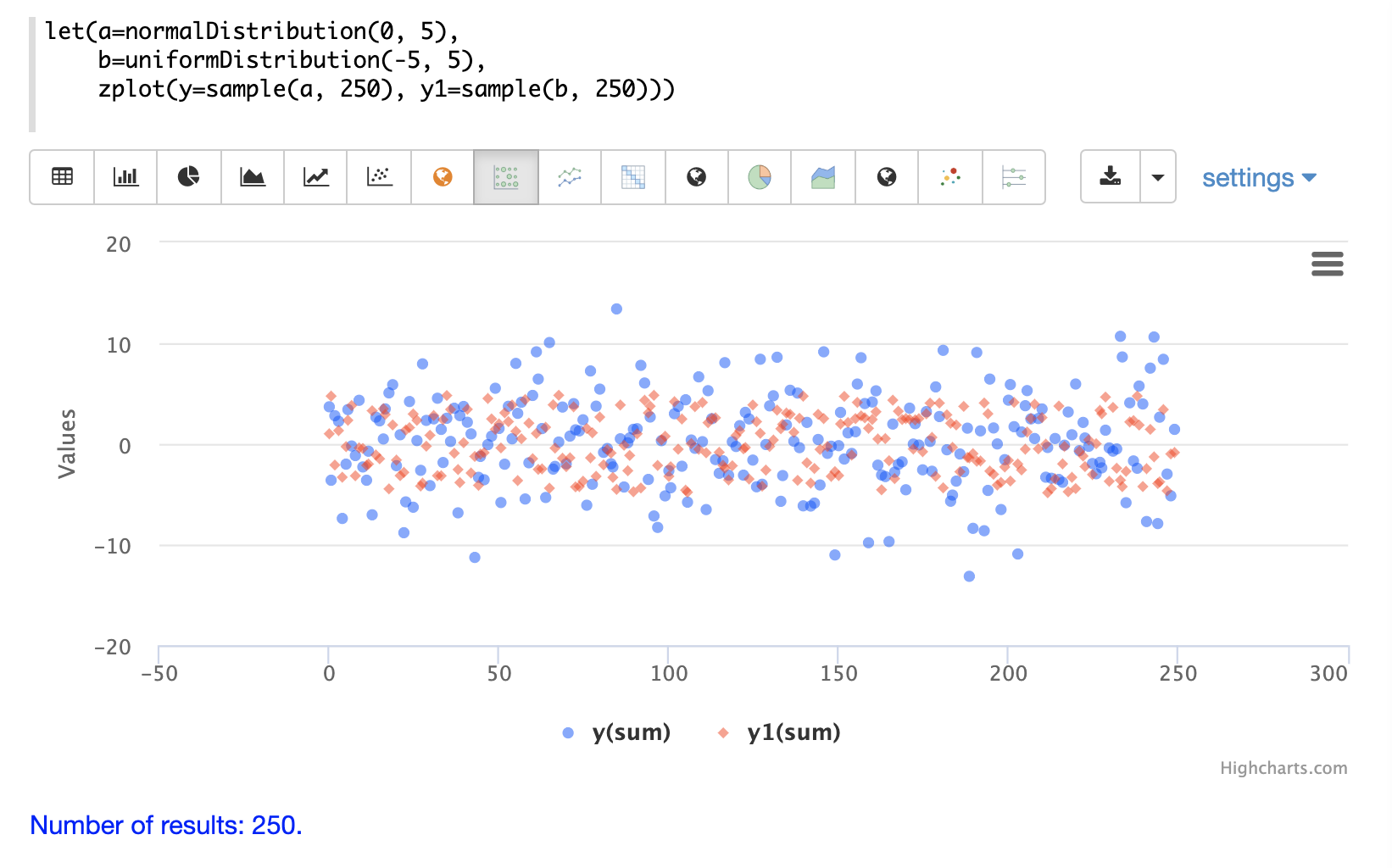
$sample overlay$

多変量正規分布

多変量正規分布は、一変量正規分布を高次元に一般化したものです。

多変量正規分布は、正規分布する2つ以上の確率変数をモデル化します。変数間の関係は、共分散行列によって定義されます。

サンプリング

sample関数は、一変量正規分布と同じように、多変量正規分布からサンプルを抽出するために使用できます。

違いは、各サンプルが、基礎となる各正規分布から抽出されたサンプルを含む配列になることです。複数のサンプルが抽出された場合、sample関数は、各行にサンプルを含む行列を返します。長期的には、サンプル行列の列は、多変量正規分布のパラメーター設定に使用された共分散行列に適合します。

以下の例では、多変量正規分布を初期化し、サンプルを抽出する方法を示します。

この例では、ログレコードのコレクションから5000個のランダムサンプルが選択されます。各サンプルには、filesize_dとresponse_dのフィールドが含まれています。両方のフィールドの値は、正規分布に適合します。

次に、両方のフィールドがベクトル化されます。filesize_dベクトルは変数bに格納され、response_d変数は変数cに格納されます。

2つのベクトル化されたフィールドの平均値を含む配列が作成されます。

次に、両方のベクトルが行列に追加され、転置されます。これにより、各行にfilesize_dとresponse_dの1つの観測値が含まれる観測行列が作成されます。次に、観測行列の列からcov関数を使用して共分散行列が作成されます。共分散行列は、filesize_dとresponse_dの間の共分散を記述します。

次に、multivariateNormalDistribution関数が、2つのフィールドの平均値の配列と共分散行列とともに呼び出されます。多変量正規分布のモデルは、変数gに割り当てられます。

最後に、多変量正規分布から5つのサンプルが抽出されます。

let(a=random(logs, q="*:*", rows="5000", fl="filesize_d, response_d"),
    b=col(a, filesize_d),
    c=col(a, response_d),
    d=array(mean(b), mean(c)),
    e=transpose(matrix(b, c)),
    f=cov(e),
    g=multiVariateNormalDistribution(d, f),
    h=sample(g, 5))

サンプルは、各行が1つのサンプルを表す行列として返されます。行列には2つの列があります。最初の列にはfilesize_dのサンプルが含まれ、2番目の列にはresponse_dのサンプルが含まれます。長期的には、列間の共分散は、多変量正規分布をインスタンス化するために使用された共分散行列に適合します。

{
  "result-set": {
    "docs": [
      {
        "h": [
          [
            41974.85669321393,
            779.4097049705296
          ],
          [
            42869.19876441414,
            834.2599296790783
          ],
          [
            38556.30444839889,
            720.3683470060988
          ],
          [
            37689.31290928216,
            686.5549428100018
          ],
          [
            40564.74398214547,
            769.9328090774
          ]
        ]
      },
      {
        "EOF": true,
        "RESPONSE_TIME": 162
      }
    ]
  }
}